人教版数学五年级下册4.1.1 分数的产生和意义(课件21张ppt)
文档属性
| 名称 | 人教版数学五年级下册4.1.1 分数的产生和意义(课件21张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-08 19:54:51 | ||
图片预览








文档简介
(共21张PPT)
课时1 分数的产生和意义
分数的意义和性质
一、复习引入
我们已经初步认识了分数。
谁来说几个分数?
那你们知道分数是怎样产生的吗?
能根据成语说出下面的分数吗?
一分为二( ) 七上八下( ) 百里挑一( ) 十拿九稳( )
二、例题讲解
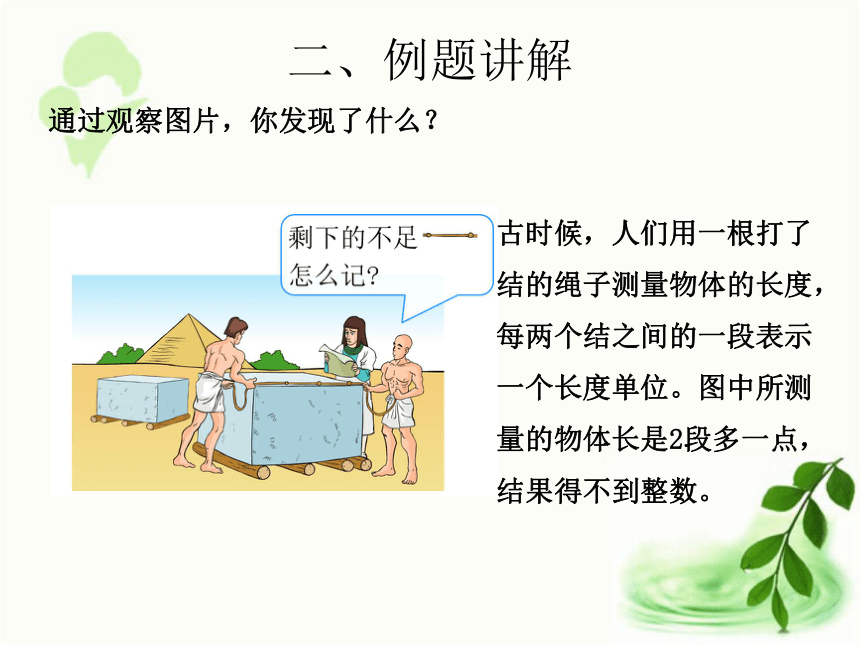
通过观察图片,你发现了什么?
古时候,人们用一根打了结的绳子测量物体的长度,每两个结之间的一段表示一个长度单位。图中所测量的物体长是2段多一点,结果得不到整数。
通过观察图片,你发现了什么?
把1个西红柿平均分给2个同学,每个同学都得不到整数个,只能分到 个
把1块月饼平均分给2个同学,每个同学都得不到整数个,只能分到 块。
通过观察图片,你发现了什么?
把1包饼干平均分给2个同学,每个同学都得不到整数个,只能分到 包。
通过观察图片,你发现了什么?
实际生活中,在进行测量、分物或计算时,往往不能正好得到整数的结果,在这种情况下就产生了分数。
【分数的产生】
【分数的应用】
在分物、测量时可以用分数,在计算过程中,也可以用分数。
【思考】你能举例说明 的含义吗?
把一张正方形纸平均分成4份,每份是这张正方形纸的 。
把一张圆形纸平均分成4份,每份是这张圆形纸的 。
【思考】你能举例说明 的含义吗?
把一条线段平均分成4份,每份是这条线段的 。
通过上面的例子你发现了什么?
我们把一个物体,(一个正方形、一个圆和一条线段等)看作一个整体,把这个整体平均分成4份,每份是它的 。
【想一想】下面的两幅图片是把什么看做一个整体?
把一把香蕉(4根)看作一个整体 。每根是这把香蕉总根数的 。
把这盘面包(8个)看作一个整体 。每份是这盘面包的 。
一个物体、一个计量单位或是一些物体等都可以看作一个整体。把这个整体平均分成若干份,这样的一份或几份都可以用分数来表示。
一个整体都可以用自然数1来表示,我们通常把它叫做单位“1”。
【做一做】
一堆糖
平均分成2份,每份是这堆糖的
( )
( )
平均分成3份,2份是这堆糖的
( )
( )
平均分成4份,3份是这堆糖的
( )
( )
平均分成6份,5份是这堆糖的
( )
( )
1
2
2
3
3
4
5
6
把单位“1”平均分成若干份,表示其中的一份的数叫分数单位。例如, 的分数单位是
分数单位就是把单位“1”平均分成若干份,表示其中1份的数,也就是单位“1”的若干分之一。
分数单位是由一个分数的分母决定的。
你能说出上面其他几个分数的分数单位吗?
三、新知应用
1.填一填。
(1)把单位“1”( )分成( ),表示这样的( )或( )的数,叫做分数。
(2) 是把单位“ 1” 平均分成( )份,表示这样( )份的数。
平均
若干份
一份
几份
7
2
一个苹果
20本书
1.填一填。
(3)把一个苹果平均分成3份,每份是一个苹果的( ),单位“1”表示( )。
(4)把20本书平均分给4个小组,3个组分得20本书的( ),单位“1”表示( )。
2. 读出下面分数,并说说它们的具体含义。
长江干流约 的水体受到不同程度的污染。
读作五分之三,表示把长江干流的水体平均分成5份,受污染的干流水体占其中的3份。
死海表层的水中含盐量达到 。
2. 读出下面分数,并说说它们的具体含义。
读作十分之三,表示把死海表层的水平均分成10份,盐占其中的3份。
3.甲班人数的 一定比乙班人数的 多吗?
不一定,因为单位“1”不一定相同。若甲班有30人,乙班有50人,那么甲班人数的五分之三就少于乙班人数的五分之二。
通过这节课的学习你有什么收获?有不懂的问题请提出来。
四、课堂小结
1.一个物体、一个计量单位或一些物体都可以看成不同的一个整体,这些不同的一个整体都可以用自然数1来表示,通常把它叫做单位“1”。
2.把单位“1”平均分成若干份,这样的一份或几份都可以用分数来表示。
1. 第47页练习十一。
2. 练习册中与本课时有关系的练习题。
五、课后作业
课时1 分数的产生和意义
分数的意义和性质
一、复习引入
我们已经初步认识了分数。
谁来说几个分数?
那你们知道分数是怎样产生的吗?
能根据成语说出下面的分数吗?
一分为二( ) 七上八下( ) 百里挑一( ) 十拿九稳( )
二、例题讲解
通过观察图片,你发现了什么?
古时候,人们用一根打了结的绳子测量物体的长度,每两个结之间的一段表示一个长度单位。图中所测量的物体长是2段多一点,结果得不到整数。
通过观察图片,你发现了什么?
把1个西红柿平均分给2个同学,每个同学都得不到整数个,只能分到 个
把1块月饼平均分给2个同学,每个同学都得不到整数个,只能分到 块。
通过观察图片,你发现了什么?
把1包饼干平均分给2个同学,每个同学都得不到整数个,只能分到 包。
通过观察图片,你发现了什么?
实际生活中,在进行测量、分物或计算时,往往不能正好得到整数的结果,在这种情况下就产生了分数。
【分数的产生】
【分数的应用】
在分物、测量时可以用分数,在计算过程中,也可以用分数。
【思考】你能举例说明 的含义吗?
把一张正方形纸平均分成4份,每份是这张正方形纸的 。
把一张圆形纸平均分成4份,每份是这张圆形纸的 。
【思考】你能举例说明 的含义吗?
把一条线段平均分成4份,每份是这条线段的 。
通过上面的例子你发现了什么?
我们把一个物体,(一个正方形、一个圆和一条线段等)看作一个整体,把这个整体平均分成4份,每份是它的 。
【想一想】下面的两幅图片是把什么看做一个整体?
把一把香蕉(4根)看作一个整体 。每根是这把香蕉总根数的 。
把这盘面包(8个)看作一个整体 。每份是这盘面包的 。
一个物体、一个计量单位或是一些物体等都可以看作一个整体。把这个整体平均分成若干份,这样的一份或几份都可以用分数来表示。
一个整体都可以用自然数1来表示,我们通常把它叫做单位“1”。
【做一做】
一堆糖
平均分成2份,每份是这堆糖的
( )
( )
平均分成3份,2份是这堆糖的
( )
( )
平均分成4份,3份是这堆糖的
( )
( )
平均分成6份,5份是这堆糖的
( )
( )
1
2
2
3
3
4
5
6
把单位“1”平均分成若干份,表示其中的一份的数叫分数单位。例如, 的分数单位是
分数单位就是把单位“1”平均分成若干份,表示其中1份的数,也就是单位“1”的若干分之一。
分数单位是由一个分数的分母决定的。
你能说出上面其他几个分数的分数单位吗?
三、新知应用
1.填一填。
(1)把单位“1”( )分成( ),表示这样的( )或( )的数,叫做分数。
(2) 是把单位“ 1” 平均分成( )份,表示这样( )份的数。
平均
若干份
一份
几份
7
2
一个苹果
20本书
1.填一填。
(3)把一个苹果平均分成3份,每份是一个苹果的( ),单位“1”表示( )。
(4)把20本书平均分给4个小组,3个组分得20本书的( ),单位“1”表示( )。
2. 读出下面分数,并说说它们的具体含义。
长江干流约 的水体受到不同程度的污染。
读作五分之三,表示把长江干流的水体平均分成5份,受污染的干流水体占其中的3份。
死海表层的水中含盐量达到 。
2. 读出下面分数,并说说它们的具体含义。
读作十分之三,表示把死海表层的水平均分成10份,盐占其中的3份。
3.甲班人数的 一定比乙班人数的 多吗?
不一定,因为单位“1”不一定相同。若甲班有30人,乙班有50人,那么甲班人数的五分之三就少于乙班人数的五分之二。
通过这节课的学习你有什么收获?有不懂的问题请提出来。
四、课堂小结
1.一个物体、一个计量单位或一些物体都可以看成不同的一个整体,这些不同的一个整体都可以用自然数1来表示,通常把它叫做单位“1”。
2.把单位“1”平均分成若干份,这样的一份或几份都可以用分数来表示。
1. 第47页练习十一。
2. 练习册中与本课时有关系的练习题。
五、课后作业
