人教版数学五年级下册5.1 旋转(例1、例2、例3)(共26张ppt)
文档属性
| 名称 | 人教版数学五年级下册5.1 旋转(例1、例2、例3)(共26张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 803.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-08 20:33:11 | ||
图片预览





文档简介
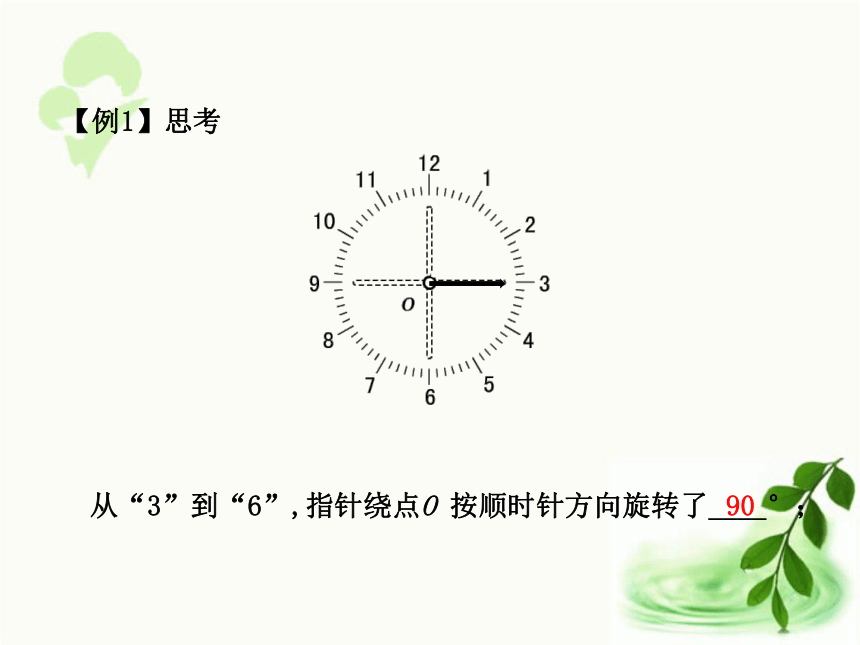
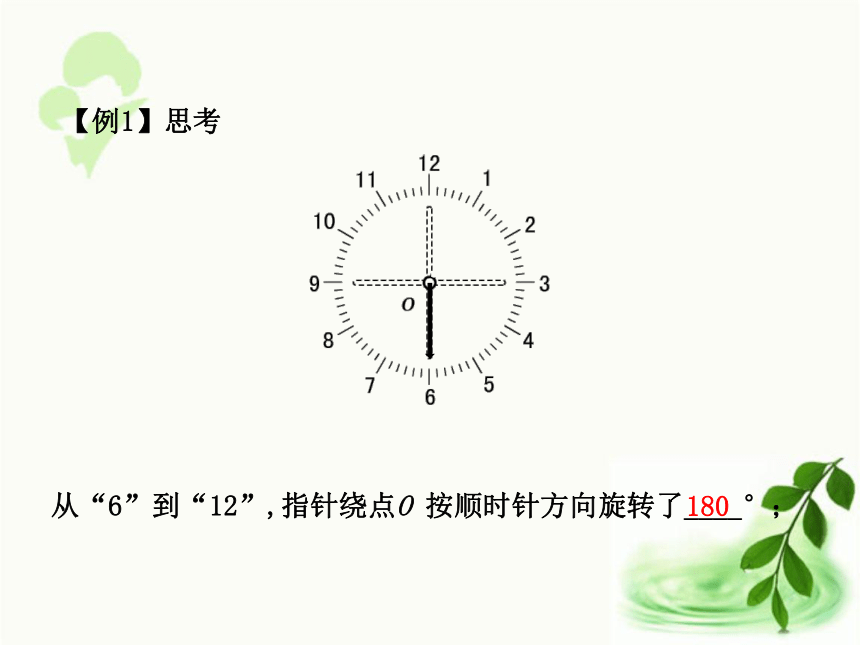
课件26张PPT。课时1 旋转图形的运动会(三)一、情境引入观察课件的演示,你看到了什么?风车是旋转现象,挡车杆是旋转现象,荡秋千是旋转现象。像钟表上指针和风车都绕着一个点或一个轴转动的这种现象就是旋转。二、例题讲解【例1】从“12”到“1”,指针绕点O 按顺时针方向旋转了30°;【例1】思考从“1”到“____”,指针绕点O 按顺时针方向旋转了60°; 3【例1】思考从“3”到“6”,指针绕点O 按顺时针方向旋转了____°; 90【例1】思考从“6”到“12”,指针绕点O 按顺时针方向旋转了____°; 180【例1】思考指针是绕哪个点旋转的?
是向什么方向旋转的?
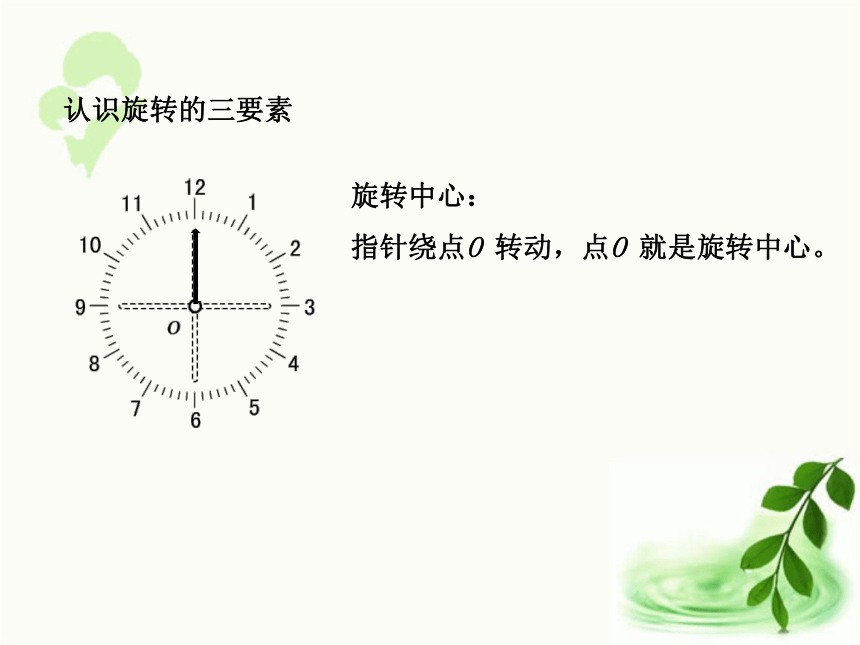
旋转了多少度?认识旋转的三要素旋转中心:
指针绕点O 转动,点O 就是旋转中心。认识旋转的三要素旋转方向:
与钟表上指针旋转方向相同的方向为顺时针方向。
与钟表上指针旋转方向相反的方向为逆时针方向。认识旋转的三要素旋转角度:
旋转前后,指针的起始位置与结束位置的夹角的度数叫做旋转角度。左侧有车通过,车杆要绕点O1按顺时针方向旋转90°。 右侧有车通过,车杆要绕点 按 方向旋转 。 【做一做】O1O2O2O1O2逆时针90°【例2】【思考】(1)观察三角尺的位置是如何变化的?
(2)你有什么发现?如上图,三角尺绕点O 转动,三角尺的两条直角边都绕点O 顺时针旋转了90°。从图中三角尺的旋转可以看出,三角尺的两条直角边都绕点O顺时针旋转了90°,旋转后图形的形状、大小都没有发生变化,只是位置变了,这就是图形旋转的特征。【例3】画出三角形AOB 绕点O 顺时针旋转90°后的图形。绕点O 旋转,点O的位置不变。找出点A 和点B 按顺时针旋转90°后的位置。(1)先画点A的对应点A′,OA′垂直于OA,点A′与点O 的距离应该是4格。A′(2)再画点B′,OB′垂直于OB,点B′与点O 的距离应该是3格。B′A′(3)连接点O 和点A′,O 和点B′,点A′和点B′在方格纸上画简单图形旋转90°后的图形的步骤:
(1)找出原图形的关键点所在的位置;
(2)根据对应点旋转90°,对应线段长度不变来找出关键点旋转后的对应点;
(3)顺次连接所画出的对应点,就得到旋转后的图形。三、新知应用1.风车绕点O( )
时针旋转 °。风车绕点O( )
时针旋转 °。逆逆90902.你能在方格纸上画出三角形AOB 绕点O 逆时针旋转90°后的图形吗?A′B′3.下面图形绕着它的中心点O旋转。(填序号)
1.旋转90°与原图形重合的是( )。
2.旋转120°与原图形重合的是( )。
3.旋转180°与原图形重合的是( )。
4.旋转360°与原图形重合的是( )。CDB CA B C D
通过这节课的学习你有什么收获?有不懂的问题请提出来。
四、课堂小结1.旋转的含义:物体绕着某一点或轴运动,这种运动现象称为旋转。
2.旋转的三要素:旋转中心、旋转方向、旋转角度。3.画简单图形旋转后的图形,首先弄清旋转点和旋转方向。
4.再找出图形的关键点或线段并画出它们旋转后的图形(垂直,长度相等)。1. 第85页练习二十一。2. 练习册中与本课时有关系的练习题。五、课后作业
是向什么方向旋转的?
旋转了多少度?认识旋转的三要素旋转中心:
指针绕点O 转动,点O 就是旋转中心。认识旋转的三要素旋转方向:
与钟表上指针旋转方向相同的方向为顺时针方向。
与钟表上指针旋转方向相反的方向为逆时针方向。认识旋转的三要素旋转角度:
旋转前后,指针的起始位置与结束位置的夹角的度数叫做旋转角度。左侧有车通过,车杆要绕点O1按顺时针方向旋转90°。 右侧有车通过,车杆要绕点 按 方向旋转 。 【做一做】O1O2O2O1O2逆时针90°【例2】【思考】(1)观察三角尺的位置是如何变化的?
(2)你有什么发现?如上图,三角尺绕点O 转动,三角尺的两条直角边都绕点O 顺时针旋转了90°。从图中三角尺的旋转可以看出,三角尺的两条直角边都绕点O顺时针旋转了90°,旋转后图形的形状、大小都没有发生变化,只是位置变了,这就是图形旋转的特征。【例3】画出三角形AOB 绕点O 顺时针旋转90°后的图形。绕点O 旋转,点O的位置不变。找出点A 和点B 按顺时针旋转90°后的位置。(1)先画点A的对应点A′,OA′垂直于OA,点A′与点O 的距离应该是4格。A′(2)再画点B′,OB′垂直于OB,点B′与点O 的距离应该是3格。B′A′(3)连接点O 和点A′,O 和点B′,点A′和点B′在方格纸上画简单图形旋转90°后的图形的步骤:
(1)找出原图形的关键点所在的位置;
(2)根据对应点旋转90°,对应线段长度不变来找出关键点旋转后的对应点;
(3)顺次连接所画出的对应点,就得到旋转后的图形。三、新知应用1.风车绕点O( )
时针旋转 °。风车绕点O( )
时针旋转 °。逆逆90902.你能在方格纸上画出三角形AOB 绕点O 逆时针旋转90°后的图形吗?A′B′3.下面图形绕着它的中心点O旋转。(填序号)
1.旋转90°与原图形重合的是( )。
2.旋转120°与原图形重合的是( )。
3.旋转180°与原图形重合的是( )。
4.旋转360°与原图形重合的是( )。CDB CA B C D
通过这节课的学习你有什么收获?有不懂的问题请提出来。
四、课堂小结1.旋转的含义:物体绕着某一点或轴运动,这种运动现象称为旋转。
2.旋转的三要素:旋转中心、旋转方向、旋转角度。3.画简单图形旋转后的图形,首先弄清旋转点和旋转方向。
4.再找出图形的关键点或线段并画出它们旋转后的图形(垂直,长度相等)。1. 第85页练习二十一。2. 练习册中与本课时有关系的练习题。五、课后作业
