人教版八年级数学下册16.1 第2课时 二次根式的性质课件(共18张PPT)
文档属性
| 名称 | 人教版八年级数学下册16.1 第2课时 二次根式的性质课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-06 12:00:04 | ||
图片预览




文档简介
(共18张PPT)
第十六章 二次根式
16.1 二根次式
第2课时 二次根式的性质
学习目标
1、理解二次根式的性质;
2、会利用性质化简和计算。
*
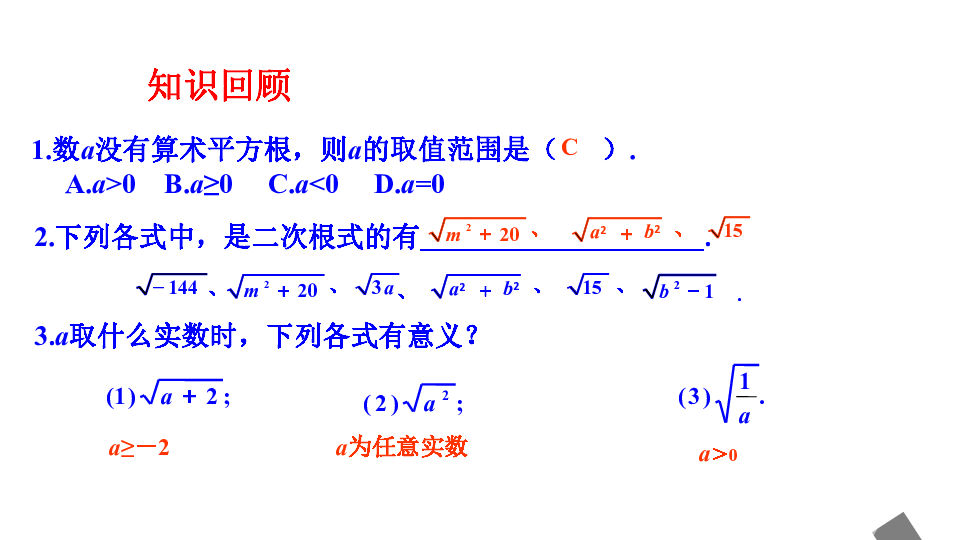
1.数a没有算术平方根,则a的取值范围是( ).
A.a>0 B.a≥0 C.a<0 D.a=0
2.下列各式中,是二次根式的有____________________.
C
3.a取什么实数时,下列各式有意义?
a≥-2
a为任意实数
a>0
知识回顾
4
2
0
是2的算术平方根,根据算术平方根的意义,
是一个平方等于2的非负数.因此 .
同理, 分别是0,4, 的算术平方根,即得上面的等式.
归纳总结
即一个非负数的算术平方根的平方等于它本身.
注意:不要忽略a≥0这一限制条件.这是使二次根式 有意义的前提条件.
例1 计算:
解:
(2)可以用到幂的哪条基本性质呢?
积的乘方:
(ab)2=a2b2
0
2
0.1
即任意一个非负数的平方的算术平方根等于它本身.
...
平方运算
算术平方根
-2
-0.1
...
2
...
观察两者有什么关系?
a(a<0)
思考:当a<0时, =
?
-a
归纳总结
a (a≥0)
-a (a<0)
即任意一个数的平方的算术平方根等于它本身的绝对值.
例3 化简:
解:
归纳概念
(1)含有表示数的字母;
(2)用基本运算符号连接数或表示数的字母.
用基本运算符号把数或表示数的字母连接起来得到的式子叫代数式.
(a≥0) ,
问题3 回顾我们学过的式子,如
这些式子有哪些共同特征?
议一议:如何区别 与 ?
从运算顺序看
从取值范围看
从运算结果看
先开方,后平方
先平方,后开方
a≥0
a取任何实数
a
|a|
意义
表示一个非负数a的算术平方根的平方
表示一个实数a的平方的算术平方根
1.在下列各式中,不是代数式的是( )
A.7 B.3>2 C. D.
B
练一练
2.如图是一圆形挂钟,正面面积为S,用代数式表示出钟的半径为__________.
3.化简:
(1) = ; (2) = ;
(3) ; (4) .
3
7
4
81
1
5、 在实数范围内分解因式:
解:
本题逆用了 在实数范围内分解因式.在实数范围内分解因式时,原来在有理数范围内分解因式的方法和公式仍然适用.
6、 已知a、b、c是△ABC的三边长,化简:
解:∵a、b、c是△ABC的三边长,
∴a+b>c,b+c>a,b+a>c,
∴原式=|a+b+c|-|b+c-a|+|c-b-a|
=a+b+c-(b+c-a)+(b+a-c)
=a+b+c-b-c+a+b+a-c
=3a+b-c.
分析:
利用三角形三边关系
三边长均为正数,a+b>c
两边之和大于第三边,b+c-a>0,c-b-a<0
课堂小结
(1)你知道了二次根式的哪些性质?
(2)运用二次根式性质进行化简需要注意什么?
(3)请谈谈发现二次根式性质的思考过程?
(4)想一想,到现在为止,你学习了哪几类字母表
示数得到的式子?说说你对代数式的认识.
第十六章 二次根式
16.1 二根次式
第2课时 二次根式的性质
学习目标
1、理解二次根式的性质;
2、会利用性质化简和计算。
*
1.数a没有算术平方根,则a的取值范围是( ).
A.a>0 B.a≥0 C.a<0 D.a=0
2.下列各式中,是二次根式的有____________________.
C
3.a取什么实数时,下列各式有意义?
a≥-2
a为任意实数
a>0
知识回顾
4
2
0
是2的算术平方根,根据算术平方根的意义,
是一个平方等于2的非负数.因此 .
同理, 分别是0,4, 的算术平方根,即得上面的等式.
归纳总结
即一个非负数的算术平方根的平方等于它本身.
注意:不要忽略a≥0这一限制条件.这是使二次根式 有意义的前提条件.
例1 计算:
解:
(2)可以用到幂的哪条基本性质呢?
积的乘方:
(ab)2=a2b2
0
2
0.1
即任意一个非负数的平方的算术平方根等于它本身.
...
平方运算
算术平方根
-2
-0.1
...
2
...
观察两者有什么关系?
a(a<0)
思考:当a<0时, =
?
-a
归纳总结
a (a≥0)
-a (a<0)
即任意一个数的平方的算术平方根等于它本身的绝对值.
例3 化简:
解:
归纳概念
(1)含有表示数的字母;
(2)用基本运算符号连接数或表示数的字母.
用基本运算符号把数或表示数的字母连接起来得到的式子叫代数式.
(a≥0) ,
问题3 回顾我们学过的式子,如
这些式子有哪些共同特征?
议一议:如何区别 与 ?
从运算顺序看
从取值范围看
从运算结果看
先开方,后平方
先平方,后开方
a≥0
a取任何实数
a
|a|
意义
表示一个非负数a的算术平方根的平方
表示一个实数a的平方的算术平方根
1.在下列各式中,不是代数式的是( )
A.7 B.3>2 C. D.
B
练一练
2.如图是一圆形挂钟,正面面积为S,用代数式表示出钟的半径为__________.
3.化简:
(1) = ; (2) = ;
(3) ; (4) .
3
7
4
81
1
5、 在实数范围内分解因式:
解:
本题逆用了 在实数范围内分解因式.在实数范围内分解因式时,原来在有理数范围内分解因式的方法和公式仍然适用.
6、 已知a、b、c是△ABC的三边长,化简:
解:∵a、b、c是△ABC的三边长,
∴a+b>c,b+c>a,b+a>c,
∴原式=|a+b+c|-|b+c-a|+|c-b-a|
=a+b+c-(b+c-a)+(b+a-c)
=a+b+c-b-c+a+b+a-c
=3a+b-c.
分析:
利用三角形三边关系
三边长均为正数,a+b>c
两边之和大于第三边,b+c-a>0,c-b-a<0
课堂小结
(1)你知道了二次根式的哪些性质?
(2)运用二次根式性质进行化简需要注意什么?
(3)请谈谈发现二次根式性质的思考过程?
(4)想一想,到现在为止,你学习了哪几类字母表
示数得到的式子?说说你对代数式的认识.
