沪科版九年级数学下册 24.2.4 圆的确定课件 ( 共22张PPT)
文档属性
| 名称 | 沪科版九年级数学下册 24.2.4 圆的确定课件 ( 共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-06 15:11:39 | ||
图片预览



文档简介
课件22张PPT。第二十四章
圆九年级数学沪科版·下册24.2.4 圆的确定教学目标1.理解并掌握三点确定圆的条件并会应用. (重点)
2.理解并掌握三角形的外接圆及外心的概念. (难点)
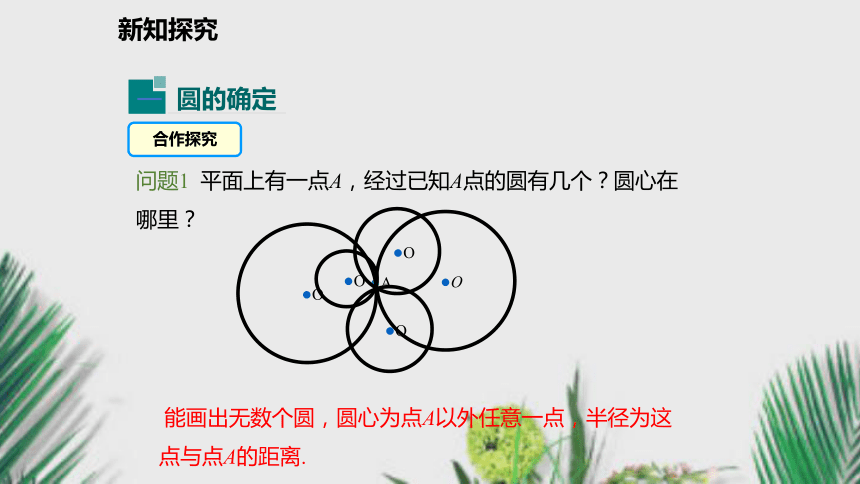
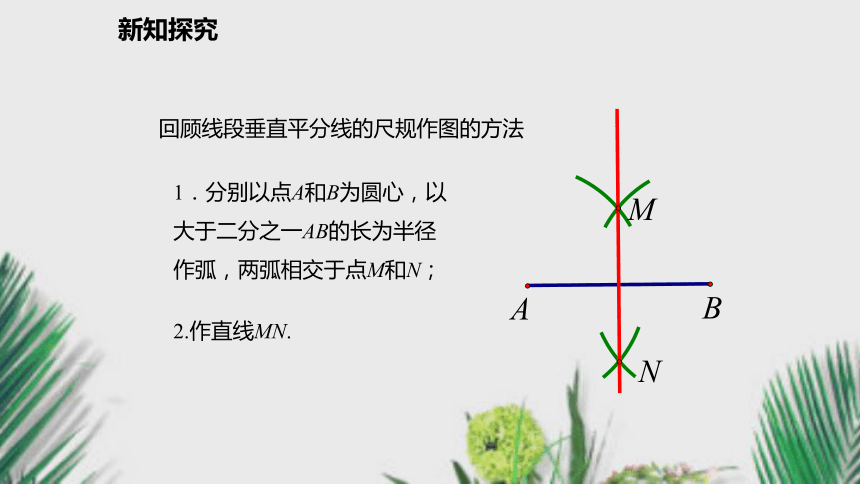
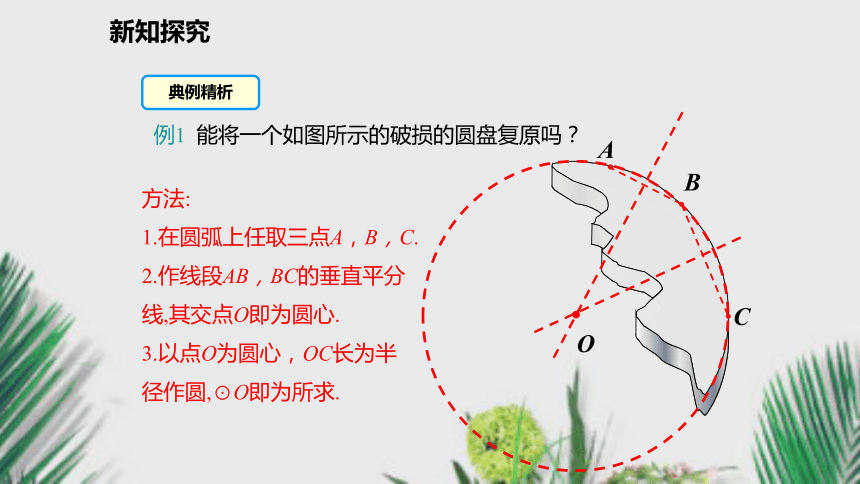
3.了解反证法的证明思想.复习导入复习引入要确定一个圆必须满足几个条件?一位考古学家在长沙马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?新知探究合作探究问题1 平面上有一点A,经过已知A点的圆有几个?圆心在哪里? ●A 能画出无数个圆,圆心为点A以外任意一点,半径为这点与点A的距离.新知探究回顾线段垂直平分线的尺规作图的方法1.分别以点A和B为圆心,以
大于二分之一AB的长为半径
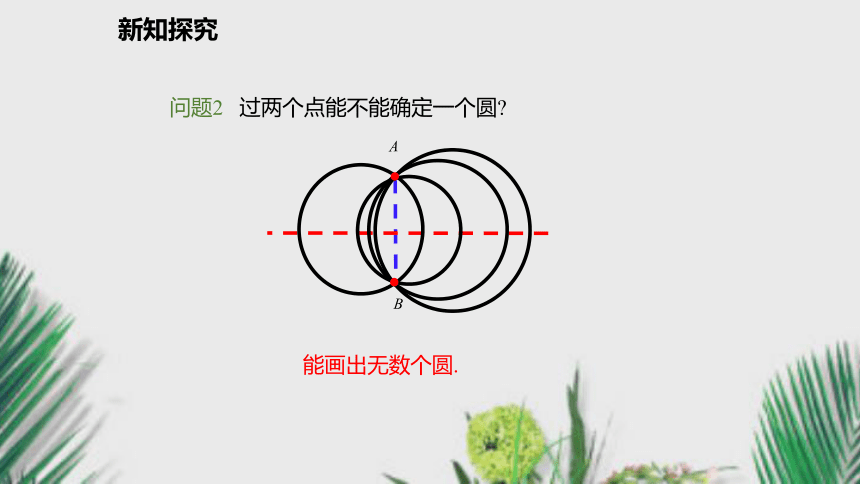
作弧,两弧相交于点M和N; 2.作直线MN.NMAB新知探究问题2 过两个点能不能确定一个圆?
能画出无数个圆.新知探究定理:
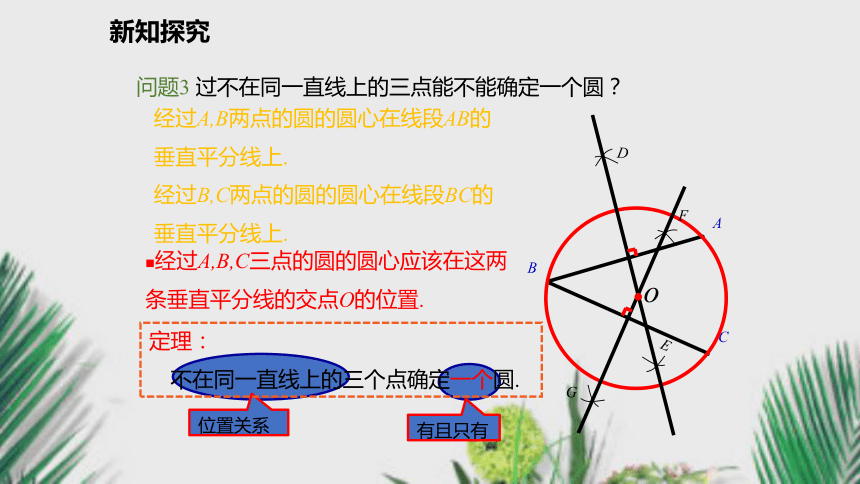
不在同一直线上的三个点确定一个圆.问题3 过不在同一直线上的三点能不能确定一个圆?●o经过B,C两点的圆的圆心在线段BC的垂直平分线上.经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.经过A,B两点的圆的圆心在线段AB的垂直平分线上.新知探究方法:
1.在圆弧上任取三点A,B,C.
2.作线段AB,BC的垂直平分线,其交点O即为圆心.
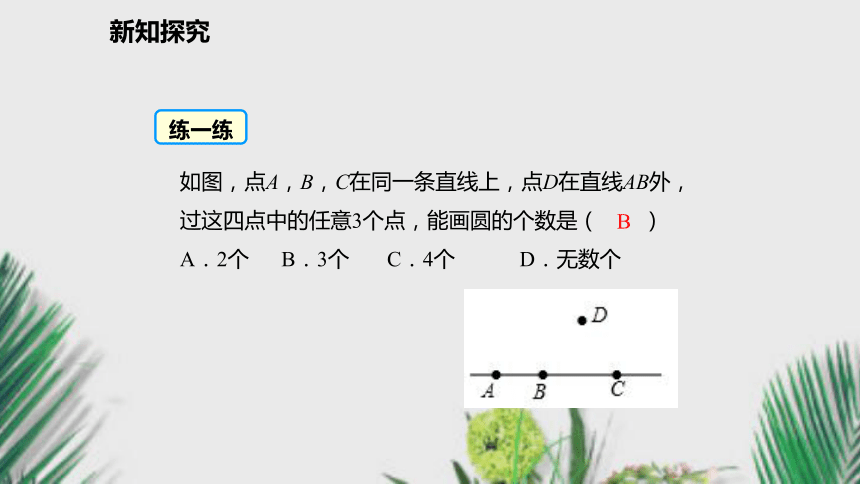
3.以点O为圆心,OC长为半径作圆,⊙O即为所求.ABCO例1 能将一个如图所示的破损的圆盘复原吗?典例精析新知探究如图,点A,B,C在同一条直线上,点D在直线AB外,过这四点中的任意3个点,能画圆的个数是( )
A.2个 B.3个 C.4个 D.无数个 练一练B新知探究 已知△ABC,用直尺与圆规作出过A,B,C三点的圆.O互动探究新知探究1. 外接圆:经过三角形三个顶点的圆
⊙O叫做△ABC的________, △ABC叫做
⊙O的____________.三角形的外心到三角形三个顶点的距离相等.2.三角形的外心:
定义:●O外接圆 内接三角形 三角形外接圆的圆心叫做三角形的外心.作图:三角形三边中垂线的交点.性质:知识要点新知探究分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系. ●O●O●O画一画锐角三角形的外心位于三角形内;
直角三角形的外心位于直角三角形斜边的中点;
钝角三角形的外心位于三角形外.新知探究例2 如图,在△ABC中,O是它的外心,BC=24cm,O到BC的距离是5cm,求△ABC的外接圆的半径.解:连接OB,过点O作OD⊥BC.D则OD=5cm,在Rt△OBD中即△ABC的外接圆的半径为13cm.解析:由外心的定义可知外接圆的半径等于OB,过点O作OD⊥BC,易得BD=12cm.由此可求它的外接圆的半径.ABCO新知探究思考:经过同一条直线上的三个点能作出一个圆吗?l1l2如图,假设过同一条直线l上三点A,B,C可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.新知探究先假设命题的结论不成立,然后经过推理,得出矛盾(常与公理、定理、定义或已知条件相矛盾)的结果,由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.反设:假设命题的结论不成立
推理:从这个假设出发,经过推理,得出矛盾
③ 结论:由矛盾判定假设不正确,从而肯定命题的结论正确知识要点 反证法的概念 反证法的一般步骤新知探究例3 用反证法证明定理“两条直线被第三条直线所截,同位角相等”. 已知,如图,直线AB∥CD,直线EF分别交AB,CD于点O1,O2.
求证:∠EO1B=∠EO2D.证明:假设∠EO1B≠∠EO2D,过点O1作直线A'B',使∠EO1B'=∠EO2D,∴A'B'∥CD.即过点O1有两条直线平行于直线CD,这与“过直线外一点有且只有一条直线与这条直线平行”相矛盾,即∠EO1B≠∠EO2D的假设不成立.∴∠EO1B=∠EO2D.A'B'课堂小结圆的确定圆的确定三角形的外接圆反证法不在同一直线上的三个点确定一个圆外接圆外心内接三角形三角形外心的到三角形的三个顶点距离相等课堂小测(1)圆心O到A,B,C三点距离 (填“相等”或”不相等”).(2)连接AB,AC,过O点分别作直线MN⊥AB, EF⊥AC,则MN是AB的 ;
EF是AC的 .(3)AB,AC的垂直平分线的交点
O到B,C的距离 .相等垂直平分线垂直平分线相等NMFE1.填空课堂小测2.下列命题不正确的是 ( )
A.过一点有无数个圆 B.过两点有无数个圆
C.弦是圆的一部分 D.过同一直线上三点不能画圆
3.三角形的外心具有的性质是 ( )
A.到三边的距离相等 B.到三个顶点的距离相等
C.外心在三角形的外 D.外心在三角形内CB课堂小测4.小颖同学在手工制作中,把一个边长为12cm的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为( )B课堂小测 5.某一个城市在一块空地新建了三个居民小区,它们分别为A,B,C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等.请问同学们这所中学应建在哪个位置?你怎么确定这个位置呢?●●●BAC如图,连接AC,AB,
作AC,AB的垂直平分线,交于点O,点O即为学校的位置.O课堂小测6.如图,已知 Rt△ABC 中 ,∠C=90°.若 AC=12cm,BC=5cm,求的外接圆半径. 解:设Rt△ABC 的外接圆的外心为O,连接OC,则OA=OB=OC.
∴O是斜边AB 的中点.
∵∠C=90°,AC=12cm,BC=5cm.
∴AB=13cm,OA=6.5cm.
故Rt△ABC 的外接圆半径为6.5cm.
2.理解并掌握三角形的外接圆及外心的概念. (难点)
3.了解反证法的证明思想.复习导入复习引入要确定一个圆必须满足几个条件?一位考古学家在长沙马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?新知探究合作探究问题1 平面上有一点A,经过已知A点的圆有几个?圆心在哪里? ●A 能画出无数个圆,圆心为点A以外任意一点,半径为这点与点A的距离.新知探究回顾线段垂直平分线的尺规作图的方法1.分别以点A和B为圆心,以
大于二分之一AB的长为半径
作弧,两弧相交于点M和N; 2.作直线MN.NMAB新知探究问题2 过两个点能不能确定一个圆?
能画出无数个圆.新知探究定理:
不在同一直线上的三个点确定一个圆.问题3 过不在同一直线上的三点能不能确定一个圆?●o经过B,C两点的圆的圆心在线段BC的垂直平分线上.经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.经过A,B两点的圆的圆心在线段AB的垂直平分线上.新知探究方法:
1.在圆弧上任取三点A,B,C.
2.作线段AB,BC的垂直平分线,其交点O即为圆心.
3.以点O为圆心,OC长为半径作圆,⊙O即为所求.ABCO例1 能将一个如图所示的破损的圆盘复原吗?典例精析新知探究如图,点A,B,C在同一条直线上,点D在直线AB外,过这四点中的任意3个点,能画圆的个数是( )
A.2个 B.3个 C.4个 D.无数个 练一练B新知探究 已知△ABC,用直尺与圆规作出过A,B,C三点的圆.O互动探究新知探究1. 外接圆:经过三角形三个顶点的圆
⊙O叫做△ABC的________, △ABC叫做
⊙O的____________.三角形的外心到三角形三个顶点的距离相等.2.三角形的外心:
定义:●O外接圆 内接三角形 三角形外接圆的圆心叫做三角形的外心.作图:三角形三边中垂线的交点.性质:知识要点新知探究分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系. ●O●O●O画一画锐角三角形的外心位于三角形内;
直角三角形的外心位于直角三角形斜边的中点;
钝角三角形的外心位于三角形外.新知探究例2 如图,在△ABC中,O是它的外心,BC=24cm,O到BC的距离是5cm,求△ABC的外接圆的半径.解:连接OB,过点O作OD⊥BC.D则OD=5cm,在Rt△OBD中即△ABC的外接圆的半径为13cm.解析:由外心的定义可知外接圆的半径等于OB,过点O作OD⊥BC,易得BD=12cm.由此可求它的外接圆的半径.ABCO新知探究思考:经过同一条直线上的三个点能作出一个圆吗?l1l2如图,假设过同一条直线l上三点A,B,C可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.新知探究先假设命题的结论不成立,然后经过推理,得出矛盾(常与公理、定理、定义或已知条件相矛盾)的结果,由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.反设:假设命题的结论不成立
推理:从这个假设出发,经过推理,得出矛盾
③ 结论:由矛盾判定假设不正确,从而肯定命题的结论正确知识要点 反证法的概念 反证法的一般步骤新知探究例3 用反证法证明定理“两条直线被第三条直线所截,同位角相等”. 已知,如图,直线AB∥CD,直线EF分别交AB,CD于点O1,O2.
求证:∠EO1B=∠EO2D.证明:假设∠EO1B≠∠EO2D,过点O1作直线A'B',使∠EO1B'=∠EO2D,∴A'B'∥CD.即过点O1有两条直线平行于直线CD,这与“过直线外一点有且只有一条直线与这条直线平行”相矛盾,即∠EO1B≠∠EO2D的假设不成立.∴∠EO1B=∠EO2D.A'B'课堂小结圆的确定圆的确定三角形的外接圆反证法不在同一直线上的三个点确定一个圆外接圆外心内接三角形三角形外心的到三角形的三个顶点距离相等课堂小测(1)圆心O到A,B,C三点距离 (填“相等”或”不相等”).(2)连接AB,AC,过O点分别作直线MN⊥AB, EF⊥AC,则MN是AB的 ;
EF是AC的 .(3)AB,AC的垂直平分线的交点
O到B,C的距离 .相等垂直平分线垂直平分线相等NMFE1.填空课堂小测2.下列命题不正确的是 ( )
A.过一点有无数个圆 B.过两点有无数个圆
C.弦是圆的一部分 D.过同一直线上三点不能画圆
3.三角形的外心具有的性质是 ( )
A.到三边的距离相等 B.到三个顶点的距离相等
C.外心在三角形的外 D.外心在三角形内CB课堂小测4.小颖同学在手工制作中,把一个边长为12cm的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为( )B课堂小测 5.某一个城市在一块空地新建了三个居民小区,它们分别为A,B,C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等.请问同学们这所中学应建在哪个位置?你怎么确定这个位置呢?●●●BAC如图,连接AC,AB,
作AC,AB的垂直平分线,交于点O,点O即为学校的位置.O课堂小测6.如图,已知 Rt△ABC 中 ,∠C=90°.若 AC=12cm,BC=5cm,求的外接圆半径. 解:设Rt△ABC 的外接圆的外心为O,连接OC,则OA=OB=OC.
∴O是斜边AB 的中点.
∵∠C=90°,AC=12cm,BC=5cm.
∴AB=13cm,OA=6.5cm.
故Rt△ABC 的外接圆半径为6.5cm.
