沪科版九年级数学下册 24.2.1圆的有关概念及点和圆的位置关系课件(共26张PPT)
文档属性
| 名称 | 沪科版九年级数学下册 24.2.1圆的有关概念及点和圆的位置关系课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-06 00:00:00 | ||
图片预览








文档简介
课件26张PPT。第二十四章
圆九年级数学沪科版·下册24.2.1圆的有关概念及点和圆的位置关系教学目标1.认识圆,理解圆的本质属性.(重点)
2.认识弦、弧、半圆、优弧、劣弧、同心圆、等圆、等
弧等与圆有关的概念,并了解它们之间的区别和联系.
(难点)
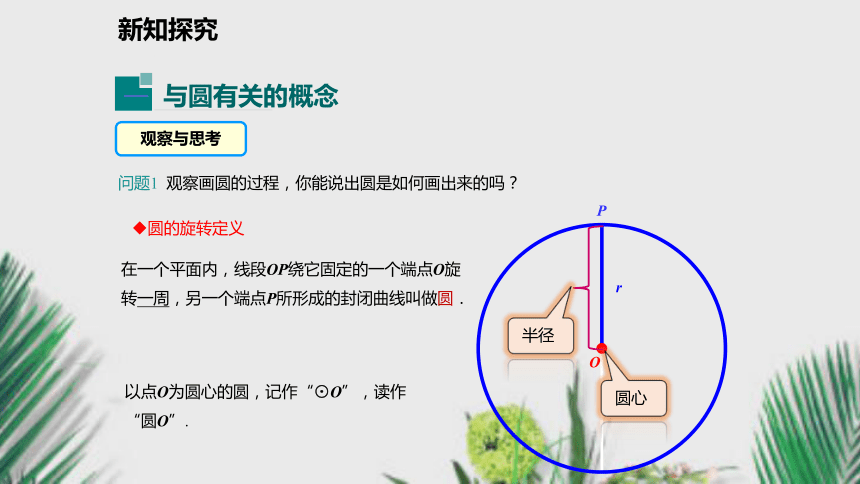
3.初步了解点与圆的位置关系.(重点)复习导入 情境引入 观察下列生活中的图片,找一找你所熟悉的图形.新知探究 我国射击运动员张梦雪在里约奥运会上获金牌,为我国赢得荣誉.如图是射击靶的示意图,它是由许多同心圆(圆心相同,半径不相同)构成的,你知道击中靶上不同位置的成绩是如何计算的吗?新知探究观察与思考·rOP圆的旋转定义在一个平面内,线段OP绕它固定的一个端点O旋转一周,另一个端点P所形成的封闭曲线叫做圆.问题1 观察画圆的过程,你能说出圆是如何画出来的吗?以点O为圆心的圆,记作“⊙O”,读作“圆O”.新知探究(1)圆上各点到定点(圆心O)的距离都等于 .
(2)到定点的距离等于定长的点都在 .平面内到定点(圆心O)的距离等于定长(半径)的所有点都在同一个圆上.OACErrrrrD定长r同一个圆上圆的集合定义问题2 从画圆的过程可以看出什么呢?·新知探究
弦: 连接圆上任意两点的线段(如图中的AC)叫做弦.经过圆心的弦(如图中的AB)叫做直径.新知探究弧: ·COAB圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做半圆.劣弧与优弧 ·COAB半圆弓形由弦及其所对的弧组成的图形叫做弓形.新知探究等圆: 能够重合的两个圆叫做等圆.容易看出:
等圆是两个半径相等的圆.等弧: 在同圆或等圆中,能够互相重合的弧叫做等弧.新知探究想一想:长度相等的弧就是等弧?ABCDADBC新知探究如图.
(1)请写出以点A为端点的优弧及劣弧;
(2)请写出以点A为端点的弦及直径. 弦AF,AB,AC.其中弦AB又是直径.(3)请任选一条弦,写出这条弦所对的弧.答案不唯一,如:弦AF,它所对的弧是 .劣弧:优弧:新知探究例1 已知,如图,AB,CD为⊙O的直径.
求证:AD∥BC.ADBCO证明:连接AC,DB. ∵AB,CD为⊙O的直径 ∴四边形ADBC为平行四边形.典例精析∴AO=OB,OC=OD. ∴AD∥BC.新知探究问题1 足球运动员踢出的足球在球场上滚动,在足球穿越中圈区(中间圆形区域)的过程中,可将足球看成一个点,这个点与圆具有怎样的位置关系?新知探究问题2 观察下图中点和圆的位置关系有哪几种?.C....B..A.点与圆的位置关系有三种:
点在圆内,点在圆上,点在圆外.新知探究⊙M,⊙N及点A,B,C,D的位置如图所示,下列说法:
(1)点A既在⊙M外也在⊙N外;
(2)点B既在⊙M上也在⊙N上;
(3)点C既在⊙M内也在⊙N内;
(4)点D既在⊙M内也在⊙N内.
其中,说法正确的有 ( )
A.1个 B.2个 C.3个 D.4个DNMCBCA新知探究问题3 设点到圆心的距离为d,圆的半径为r,量一量在点和圆三种不同位置关系时,d与r有怎样的数量关系?点P在☉O内 点P在☉O上 点P在☉O外 d d drpdd Prd<r r =>r反过来,由d与r的数量关系,怎样判定点与圆的位置关系呢?新知探究1.⊙O的半径为10cm,A,B,C三点到圆心的距离分别为8cm,10cm,12cm,则点A,B,C与⊙O的位置关系是:点A在 ;点B在 ;点C在 . 圆内圆上圆外2.圆心为O的两个同心圆,半径分别为1和2,若OP= ,则点P在( )
A.在大圆内 B.在小圆内
C.小圆外 D.大圆内,小圆外D新知探究数形结合:位置关系点与圆的位置关系
新知探究例2 如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,以点A为圆心、3cm为半径画圆,并判断:
(1)点C与⊙A的位置关系;
(2)点B与⊙A的位置关系;
(3)AB的中点D与⊙A的位置关系.●BADC解:已知⊙A的半径r=3 cm.
(1) 因为 ,
所以点C在⊙A上.
(2) 因为AB=5 cm>3 cm=r,所以点B在⊙A外.
(3)因为 ,所以点D在⊙A内.新知探究 在Rt△ABC中,∠A=30°,∠C=90°,BC=2,以点A为圆心r为半径画圆,使点C在⊙A内而点B在⊙A外,则r的取值范围为___ ___.解析:利用锐角三角函数与勾股定理,求得AB=4,AC= ,则r的取值范围为AC<r<AB,即 .拓展:课堂小结圆定义旋转定义集合定义有关
概念直径是圆中最长的弦弧半圆是特殊的弧劣弧半圆优弧弓形点与圆的位置关系弦(直径)等圆等弧课堂小测1.填空:
(1)______是圆中最长的弦,它是______的2倍.
(2)图中有 条直径, 条非直径的弦,
圆中以A为一个端点的优弧有 条,
劣弧有 条.
直径半径一二四四2.一点和⊙O上的最近点距离为4cm,最远的距离为10cm, 则这个圆的半径是 .7cm或3cm课堂小测 3.正方形ABCD的边长为2cm,以A为圆心2cm为半径作☉A,则点B在☉A ;点C在☉A ;点D在☉A .上外上4.☉O的半径r为5㎝,O为原点,点P的坐标为(3,4),则点P与☉O的位置关系为 ( )
A.在☉O内 B.在☉O上
C.在☉O外 D.在☉O上或☉O外 B课堂小测 5.一些学生正在做投圈游戏,他们呈“一”字排开.这样的队形对每一人都公平吗?你认为他们应当排成什么样的队形?不公平,应该站成圆形.课堂小测·2cm3cm6.画出由所有到已知点的距离大于或等于2cm并且小于或等于3cm的点组成的图形.O课堂小测7.如图点O处有一灯塔,警示⊙O内部为危险区,一渔船误入危险区点P处,该渔船应该按什么方向航行才能尽快离开危险区?试说明理由.解:渔船应沿着灯塔O过点P的射线OP方向航行才能尽快离开危险区.理由如下:
设射线OP交⊙O于点A,过点P任意作一条弦CD,连接OD.
在△ODP中,OD-OP<PD,又∵OD=OA,
∴OA-OP<PD,∴PA<PD ,
即渔船沿射线OP方向航行才能尽快离开危险区. ODPCA
2.认识弦、弧、半圆、优弧、劣弧、同心圆、等圆、等
弧等与圆有关的概念,并了解它们之间的区别和联系.
(难点)
3.初步了解点与圆的位置关系.(重点)复习导入 情境引入 观察下列生活中的图片,找一找你所熟悉的图形.新知探究 我国射击运动员张梦雪在里约奥运会上获金牌,为我国赢得荣誉.如图是射击靶的示意图,它是由许多同心圆(圆心相同,半径不相同)构成的,你知道击中靶上不同位置的成绩是如何计算的吗?新知探究观察与思考·rOP圆的旋转定义在一个平面内,线段OP绕它固定的一个端点O旋转一周,另一个端点P所形成的封闭曲线叫做圆.问题1 观察画圆的过程,你能说出圆是如何画出来的吗?以点O为圆心的圆,记作“⊙O”,读作“圆O”.新知探究(1)圆上各点到定点(圆心O)的距离都等于 .
(2)到定点的距离等于定长的点都在 .平面内到定点(圆心O)的距离等于定长(半径)的所有点都在同一个圆上.OACErrrrrD定长r同一个圆上圆的集合定义问题2 从画圆的过程可以看出什么呢?·新知探究
弦: 连接圆上任意两点的线段(如图中的AC)叫做弦.经过圆心的弦(如图中的AB)叫做直径.新知探究弧: ·COAB圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做半圆.劣弧与优弧 ·COAB半圆弓形由弦及其所对的弧组成的图形叫做弓形.新知探究等圆: 能够重合的两个圆叫做等圆.容易看出:
等圆是两个半径相等的圆.等弧: 在同圆或等圆中,能够互相重合的弧叫做等弧.新知探究想一想:长度相等的弧就是等弧?ABCDADBC新知探究如图.
(1)请写出以点A为端点的优弧及劣弧;
(2)请写出以点A为端点的弦及直径. 弦AF,AB,AC.其中弦AB又是直径.(3)请任选一条弦,写出这条弦所对的弧.答案不唯一,如:弦AF,它所对的弧是 .劣弧:优弧:新知探究例1 已知,如图,AB,CD为⊙O的直径.
求证:AD∥BC.ADBCO证明:连接AC,DB. ∵AB,CD为⊙O的直径 ∴四边形ADBC为平行四边形.典例精析∴AO=OB,OC=OD. ∴AD∥BC.新知探究问题1 足球运动员踢出的足球在球场上滚动,在足球穿越中圈区(中间圆形区域)的过程中,可将足球看成一个点,这个点与圆具有怎样的位置关系?新知探究问题2 观察下图中点和圆的位置关系有哪几种?.C....B..A.点与圆的位置关系有三种:
点在圆内,点在圆上,点在圆外.新知探究⊙M,⊙N及点A,B,C,D的位置如图所示,下列说法:
(1)点A既在⊙M外也在⊙N外;
(2)点B既在⊙M上也在⊙N上;
(3)点C既在⊙M内也在⊙N内;
(4)点D既在⊙M内也在⊙N内.
其中,说法正确的有 ( )
A.1个 B.2个 C.3个 D.4个DNMCBCA新知探究问题3 设点到圆心的距离为d,圆的半径为r,量一量在点和圆三种不同位置关系时,d与r有怎样的数量关系?点P在☉O内 点P在☉O上 点P在☉O外 d d drpdd Prd<r r =>r反过来,由d与r的数量关系,怎样判定点与圆的位置关系呢?新知探究1.⊙O的半径为10cm,A,B,C三点到圆心的距离分别为8cm,10cm,12cm,则点A,B,C与⊙O的位置关系是:点A在 ;点B在 ;点C在 . 圆内圆上圆外2.圆心为O的两个同心圆,半径分别为1和2,若OP= ,则点P在( )
A.在大圆内 B.在小圆内
C.小圆外 D.大圆内,小圆外D新知探究数形结合:位置关系点与圆的位置关系
新知探究例2 如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,以点A为圆心、3cm为半径画圆,并判断:
(1)点C与⊙A的位置关系;
(2)点B与⊙A的位置关系;
(3)AB的中点D与⊙A的位置关系.●BADC解:已知⊙A的半径r=3 cm.
(1) 因为 ,
所以点C在⊙A上.
(2) 因为AB=5 cm>3 cm=r,所以点B在⊙A外.
(3)因为 ,所以点D在⊙A内.新知探究 在Rt△ABC中,∠A=30°,∠C=90°,BC=2,以点A为圆心r为半径画圆,使点C在⊙A内而点B在⊙A外,则r的取值范围为___ ___.解析:利用锐角三角函数与勾股定理,求得AB=4,AC= ,则r的取值范围为AC<r<AB,即 .拓展:课堂小结圆定义旋转定义集合定义有关
概念直径是圆中最长的弦弧半圆是特殊的弧劣弧半圆优弧弓形点与圆的位置关系弦(直径)等圆等弧课堂小测1.填空:
(1)______是圆中最长的弦,它是______的2倍.
(2)图中有 条直径, 条非直径的弦,
圆中以A为一个端点的优弧有 条,
劣弧有 条.
直径半径一二四四2.一点和⊙O上的最近点距离为4cm,最远的距离为10cm, 则这个圆的半径是 .7cm或3cm课堂小测 3.正方形ABCD的边长为2cm,以A为圆心2cm为半径作☉A,则点B在☉A ;点C在☉A ;点D在☉A .上外上4.☉O的半径r为5㎝,O为原点,点P的坐标为(3,4),则点P与☉O的位置关系为 ( )
A.在☉O内 B.在☉O上
C.在☉O外 D.在☉O上或☉O外 B课堂小测 5.一些学生正在做投圈游戏,他们呈“一”字排开.这样的队形对每一人都公平吗?你认为他们应当排成什么样的队形?不公平,应该站成圆形.课堂小测·2cm3cm6.画出由所有到已知点的距离大于或等于2cm并且小于或等于3cm的点组成的图形.O课堂小测7.如图点O处有一灯塔,警示⊙O内部为危险区,一渔船误入危险区点P处,该渔船应该按什么方向航行才能尽快离开危险区?试说明理由.解:渔船应沿着灯塔O过点P的射线OP方向航行才能尽快离开危险区.理由如下:
设射线OP交⊙O于点A,过点P任意作一条弦CD,连接OD.
在△ODP中,OD-OP<PD,又∵OD=OA,
∴OA-OP<PD,∴PA<PD ,
即渔船沿射线OP方向航行才能尽快离开危险区. ODPCA
