沪科版九年级数学下册 24.2.2 垂径定理课件 (22张PPT)
文档属性
| 名称 | 沪科版九年级数学下册 24.2.2 垂径定理课件 (22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-06 15:14:45 | ||
图片预览




文档简介
课件22张PPT。第二十四章
圆九年级数学沪科版·下册24.2.2垂径定理教学目标1.进一步认识圆,了解圆是轴对称图形.
2.理解垂直于弦的直径的性质和推论,并能应用它解决一
些简单的计算、证明和作图问题.(重点)
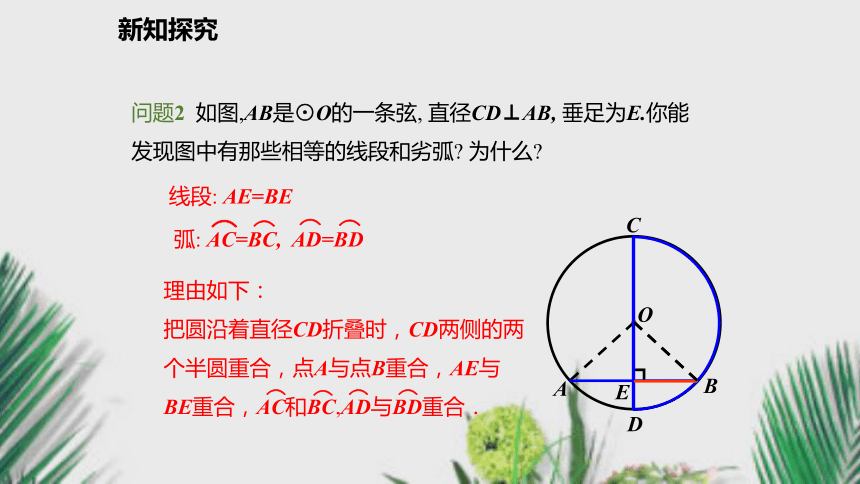
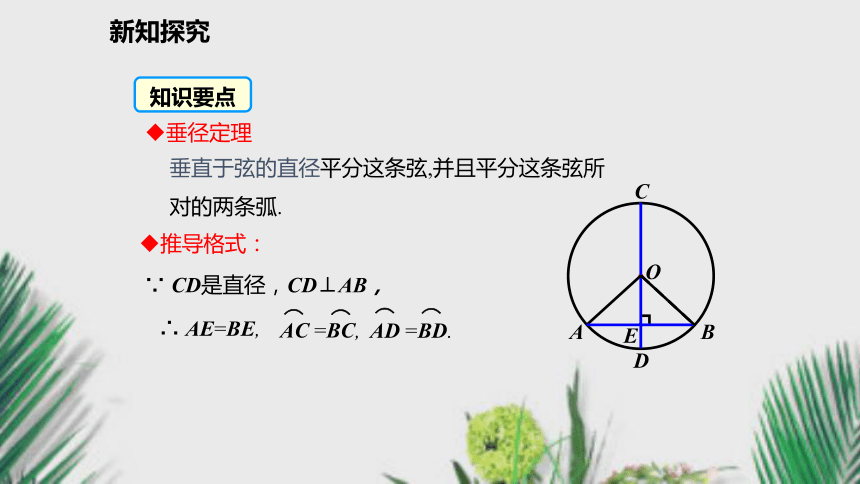
3.灵活运用垂径定理解决有关圆的问题.(难点)问题引入 赵州桥主桥拱的半径是多少? 问题:你知道赵州桥吗? 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵州桥主桥拱的半径吗?复习导入新知探究互动探究 可以发现:圆是轴对称图形.任何一条直径所在直线都是它的对称轴.问题1 剪一个圆形纸片,沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?你能证明这个结论吗?新知探究问题2 如图,AB是⊙O的一条弦, 直径CD⊥AB, 垂足为E.你能发现图中有那些相等的线段和劣弧? 为什么?线段: AE=BE·OABDEC新知探究垂径定理垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧. ∵ CD是直径,CD⊥AB,
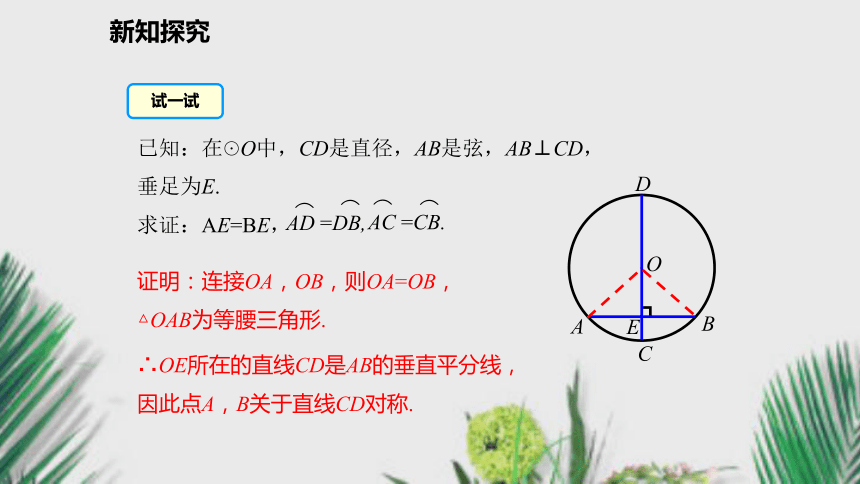
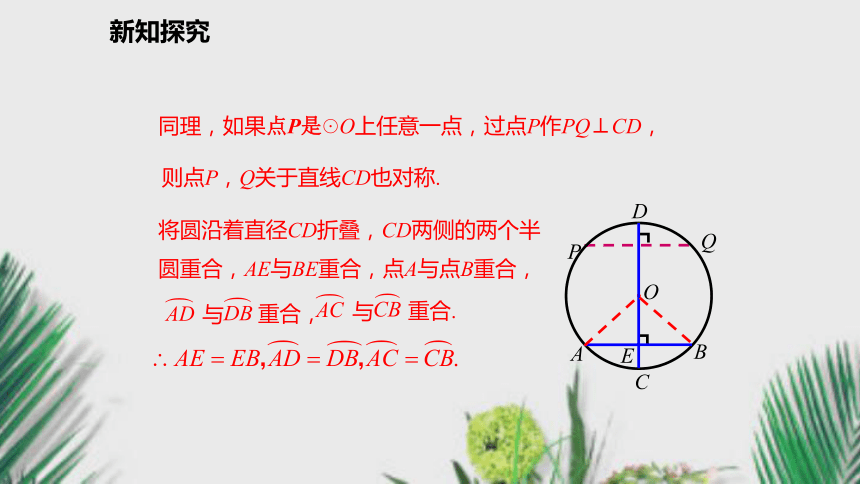
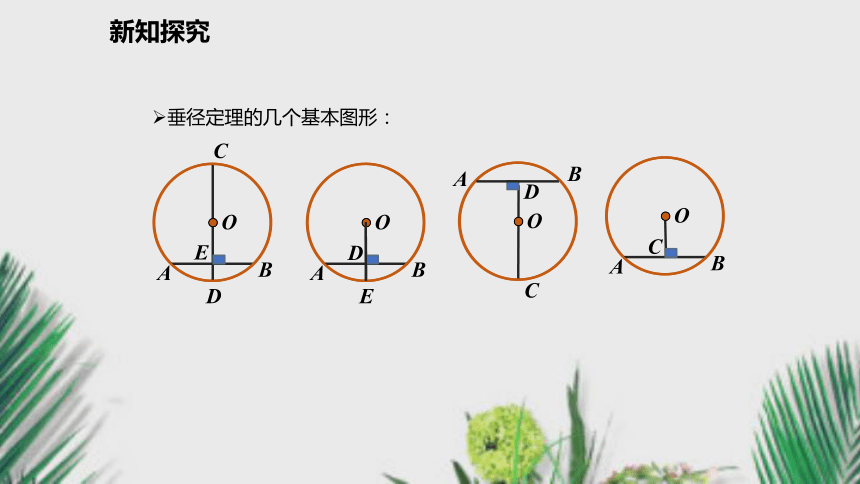
∴ AE=BE,推导格式:知识要点新知探究证明:连接OA,OB,则OA=OB,△OAB为等腰三角形.∴OE所在的直线CD是AB的垂直平分线,因此点A,B关于直线CD对称.试一试新知探究P Q 同理,如果点P是☉O上任意一点,过点P作PQ⊥CD,则点P,Q关于直线CD也对称.将圆沿着直径CD折叠,CD两侧的两个半圆重合,AE与BE重合,点A与点B重合,新知探究垂径定理的几个基本图形:新知探究证明:连接OA,OB,CA,CB,则OA=OB.即△AOB是等腰三角形.∵P是AB的中点,∴AB⊥CD.即AP=BP,∵ CD是直径,AB⊥CD,新知探究思考:“不是直径”这个条件能去掉吗?如果不能,请举出反例. 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.垂径定理的推论特别说明:
圆的两条直径是互相平分的.知识要点新知探究例1 如图,☉O中的半径为5cm,弦AB是为6cm,求圆心O到弦AB的距离.解:连接OA,过圆心O作OE⊥AB,垂足为E.E∵OA=5cm,在Rt△OEA中,有答:圆心O到弦AB的距离为4cm.弦心距新知探究例2 如图, ⊙ O的弦AB=8cm ,直径CE⊥AB于D,DC=2cm,求半径OC的长.解:连接OA,∵ CE⊥AB于D,∴设OC=xcm,则OD=x-2,根据勾股定理,得解得 x=5,即半径OC的长为5cm.x2=42+(x-2)2,新知探究例3 赵州桥建于1400年前的隋朝,是我国石拱桥中的代表性桥梁.桥的下部呈圆弧形,桥的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,求赵州桥桥拱所在圆的半径.(精确到0.1m)新知探究解:如图,用AB表示主桥拱,设AB所在圆的圆心为O,半径为R.经过圆心O作弦AB的垂线OC垂足为D,与弧AB交于点C,则D是AB的中点,C是弧AB的中点,CD就是拱高.∴ AB=37.4m,CD=7.2m.∴ AD= AB=18.7m,OD=OC-CD=R-7.2.新知探究解得R≈27.9(m).答:赵州桥桥拱所在圆的半径约为27.9m.R2=18.72+(R-7.2)2 ∵新知探究 在圆中有关弦长a,半径r, 弦心距d(圆心到弦的距离),弓形高h的计算题时,常常通过连半径或作弦心距构造直角三角形,利用垂径定理和勾股定理求解.涉及垂径定理时辅助线的添加方法弦a,弦心距d,弓形高h,半径r之间有以下关系:弓形中重要数量关系 d+h=r 新知探究 如图a,b,一弓形弦长为 cm,弓形所在的圆的半径为7cm,则弓形的高为_____________. 2cm或12cm 练一练课堂小结垂径定理内容推论辅助线一条直线满足:①过圆心;②垂直于弦; ③平分弦(不是直径); ④平分弦所对的优弧;⑤平分弦所对的劣弧.满足其中两个条件就可以推出其它三个结论.(“知二推三”)垂直于弦的直径平分这条弦,
并且平分这条弦所对的两条弧.两条辅助线:
连半径,作弦心距构造直角三角形利用勾股定理计算或建立方程.基本图形及变式图形课堂小测1.已知☉O中,弦AB=8cm,圆心到AB的距离为3cm,则此圆的半径为 .5cm2.☉O的直径AB=20cm, ∠BAC=30°,则弦AC= . 3.(分类讨论题)已知☉O的半径为10cm,弦MN∥EF,且MN=12cm,EF=16cm,则弦MN和EF之间的距离为 .14cm或2cm课堂小测4.如图,在⊙O中,AB,AC是互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证:四边形ADOE是正方形.·OABCDE证明:∴四边形ADOE为矩形,又∵AC=AB,∴ AE=AD.∴ 四边形ADOE为正方形.,,,,.课堂小测 5.如图,一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD,垂足为F,EF=90m.求这段弯路的半径.解:连接OC.设这段弯路的半径为Rm,则OF=(R-90)m.根据勾股定理,得解得R=545.∴这段弯路的半径为545m.∵CD⊥OE,
2.理解垂直于弦的直径的性质和推论,并能应用它解决一
些简单的计算、证明和作图问题.(重点)
3.灵活运用垂径定理解决有关圆的问题.(难点)问题引入 赵州桥主桥拱的半径是多少? 问题:你知道赵州桥吗? 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵州桥主桥拱的半径吗?复习导入新知探究互动探究 可以发现:圆是轴对称图形.任何一条直径所在直线都是它的对称轴.问题1 剪一个圆形纸片,沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?你能证明这个结论吗?新知探究问题2 如图,AB是⊙O的一条弦, 直径CD⊥AB, 垂足为E.你能发现图中有那些相等的线段和劣弧? 为什么?线段: AE=BE·OABDEC新知探究垂径定理垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧. ∵ CD是直径,CD⊥AB,
∴ AE=BE,推导格式:知识要点新知探究证明:连接OA,OB,则OA=OB,△OAB为等腰三角形.∴OE所在的直线CD是AB的垂直平分线,因此点A,B关于直线CD对称.试一试新知探究P Q 同理,如果点P是☉O上任意一点,过点P作PQ⊥CD,则点P,Q关于直线CD也对称.将圆沿着直径CD折叠,CD两侧的两个半圆重合,AE与BE重合,点A与点B重合,新知探究垂径定理的几个基本图形:新知探究证明:连接OA,OB,CA,CB,则OA=OB.即△AOB是等腰三角形.∵P是AB的中点,∴AB⊥CD.即AP=BP,∵ CD是直径,AB⊥CD,新知探究思考:“不是直径”这个条件能去掉吗?如果不能,请举出反例. 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.垂径定理的推论特别说明:
圆的两条直径是互相平分的.知识要点新知探究例1 如图,☉O中的半径为5cm,弦AB是为6cm,求圆心O到弦AB的距离.解:连接OA,过圆心O作OE⊥AB,垂足为E.E∵OA=5cm,在Rt△OEA中,有答:圆心O到弦AB的距离为4cm.弦心距新知探究例2 如图, ⊙ O的弦AB=8cm ,直径CE⊥AB于D,DC=2cm,求半径OC的长.解:连接OA,∵ CE⊥AB于D,∴设OC=xcm,则OD=x-2,根据勾股定理,得解得 x=5,即半径OC的长为5cm.x2=42+(x-2)2,新知探究例3 赵州桥建于1400年前的隋朝,是我国石拱桥中的代表性桥梁.桥的下部呈圆弧形,桥的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,求赵州桥桥拱所在圆的半径.(精确到0.1m)新知探究解:如图,用AB表示主桥拱,设AB所在圆的圆心为O,半径为R.经过圆心O作弦AB的垂线OC垂足为D,与弧AB交于点C,则D是AB的中点,C是弧AB的中点,CD就是拱高.∴ AB=37.4m,CD=7.2m.∴ AD= AB=18.7m,OD=OC-CD=R-7.2.新知探究解得R≈27.9(m).答:赵州桥桥拱所在圆的半径约为27.9m.R2=18.72+(R-7.2)2 ∵新知探究 在圆中有关弦长a,半径r, 弦心距d(圆心到弦的距离),弓形高h的计算题时,常常通过连半径或作弦心距构造直角三角形,利用垂径定理和勾股定理求解.涉及垂径定理时辅助线的添加方法弦a,弦心距d,弓形高h,半径r之间有以下关系:弓形中重要数量关系 d+h=r 新知探究 如图a,b,一弓形弦长为 cm,弓形所在的圆的半径为7cm,则弓形的高为_____________. 2cm或12cm 练一练课堂小结垂径定理内容推论辅助线一条直线满足:①过圆心;②垂直于弦; ③平分弦(不是直径); ④平分弦所对的优弧;⑤平分弦所对的劣弧.满足其中两个条件就可以推出其它三个结论.(“知二推三”)垂直于弦的直径平分这条弦,
并且平分这条弦所对的两条弧.两条辅助线:
连半径,作弦心距构造直角三角形利用勾股定理计算或建立方程.基本图形及变式图形课堂小测1.已知☉O中,弦AB=8cm,圆心到AB的距离为3cm,则此圆的半径为 .5cm2.☉O的直径AB=20cm, ∠BAC=30°,则弦AC= . 3.(分类讨论题)已知☉O的半径为10cm,弦MN∥EF,且MN=12cm,EF=16cm,则弦MN和EF之间的距离为 .14cm或2cm课堂小测4.如图,在⊙O中,AB,AC是互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证:四边形ADOE是正方形.·OABCDE证明:∴四边形ADOE为矩形,又∵AC=AB,∴ AE=AD.∴ 四边形ADOE为正方形.,,,,.课堂小测 5.如图,一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD,垂足为F,EF=90m.求这段弯路的半径.解:连接OC.设这段弯路的半径为Rm,则OF=(R-90)m.根据勾股定理,得解得R=545.∴这段弯路的半径为545m.∵CD⊥OE,
