人教版七年级下数学教学讲义,复习补习资料(含典型例题,巩固练习):08【提高】平面直角坐标系(含解析)
文档属性
| 名称 | 人教版七年级下数学教学讲义,复习补习资料(含典型例题,巩固练习):08【提高】平面直角坐标系(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 292.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-06 15:17:32 | ||
图片预览


文档简介
平面直角坐标系(提高)知识讲解
【学习目标】
1.理解平面直角坐标系概念,能正确画出平面直角坐标系.
2.能在平面直角坐标系中,根据坐标确定点,以及由点求出坐标,掌握点的坐标特征.
3.由数轴到平面直角坐标系,渗透类比的数学思想.
【典型例题】
类型一、有序数对表示位置
1.如图是小刚的一张笑脸,他对妹妹说:如果我用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成( ).
A.(1,0) B.(-1,0) C.(-1,1) D.(1,-1)
【思路点拨】由(0,2)表示左眼,用(2,2)表示右眼,可以确定平面直角坐标系中x轴与y轴的位置,从而可以确定嘴的位置.
【答案】A.
【解析】
解:根据(0,2)表示左眼,用(2,2)表示右眼, 可得嘴的坐标是(1,0), 故答案为A.
【总结升华】此题考查了坐标确定位置,由已知条件正确确定坐标轴的位置是解决本题的关键.
类型二、平面直角坐标系与点的坐标的概念
2.有一个长方形ABCD,长为5,宽为3,先建立一个平面直角坐标系,在此坐标系下求出A,B,C,D各点的坐标.
【答案与解析】
解:本题答案不唯一,现列举三种解法.
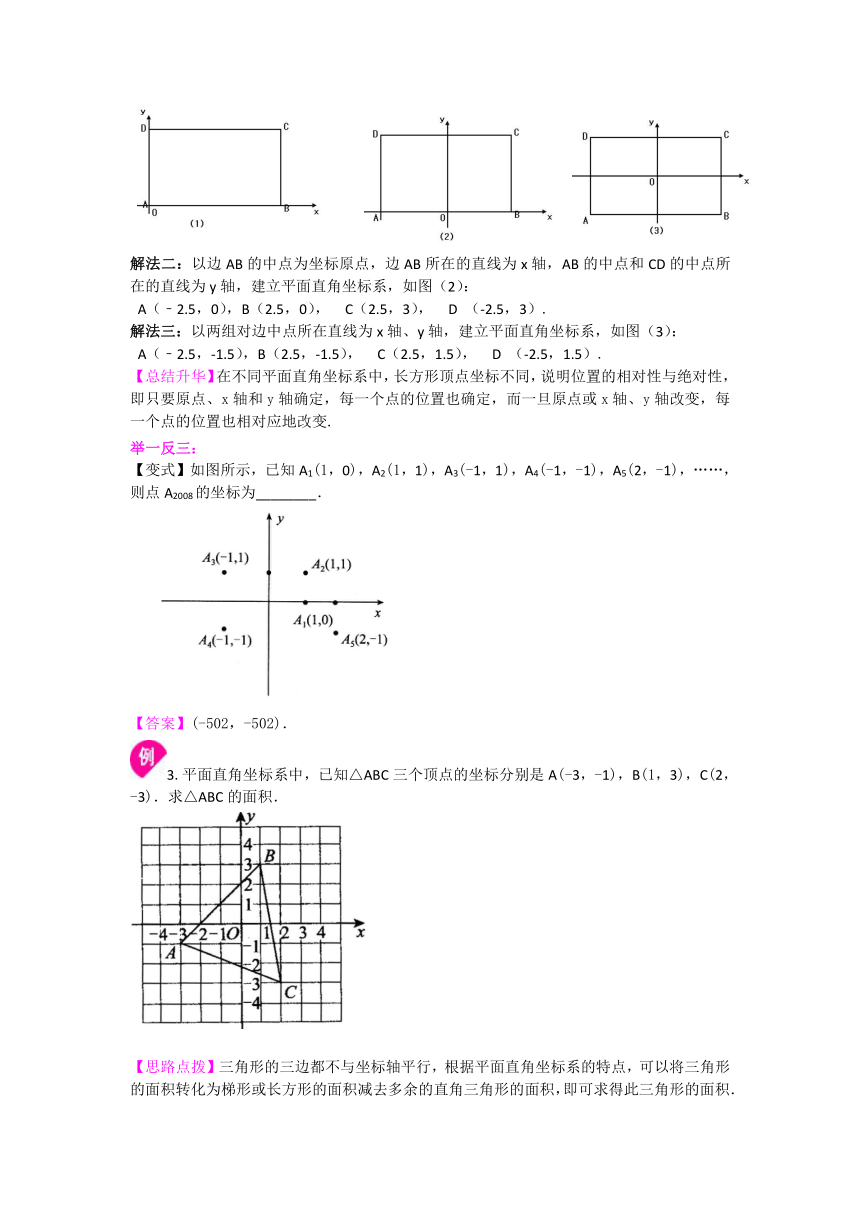
解法一:以点A为坐标原点,边AB所在的直线为x轴,边AD所在直线为y轴,建立平面直角坐标系,如图(1):
A(0,0),B(5,0), C(5,3), D (0,3).
解法二:以边AB的中点为坐标原点,边AB所在的直线为x轴,AB的中点和CD的中点所在的直线为y轴,建立平面直角坐标系,如图(2):
A(﹣2.5,0),B(2.5,0), C(2.5,3), D (-2.5,3).
解法三:以两组对边中点所在直线为x轴、y轴,建立平面直角坐标系,如图(3):
A(﹣2.5,-1.5),B(2.5,-1.5), C(2.5,1.5), D (-2.5,1.5).
【总结升华】在不同平面直角坐标系中,长方形顶点坐标不同,说明位置的相对性与绝对性,即只要原点、x轴和y轴确定,每一个点的位置也确定,而一旦原点或x轴、y轴改变,每一个点的位置也相对应地改变.
举一反三:
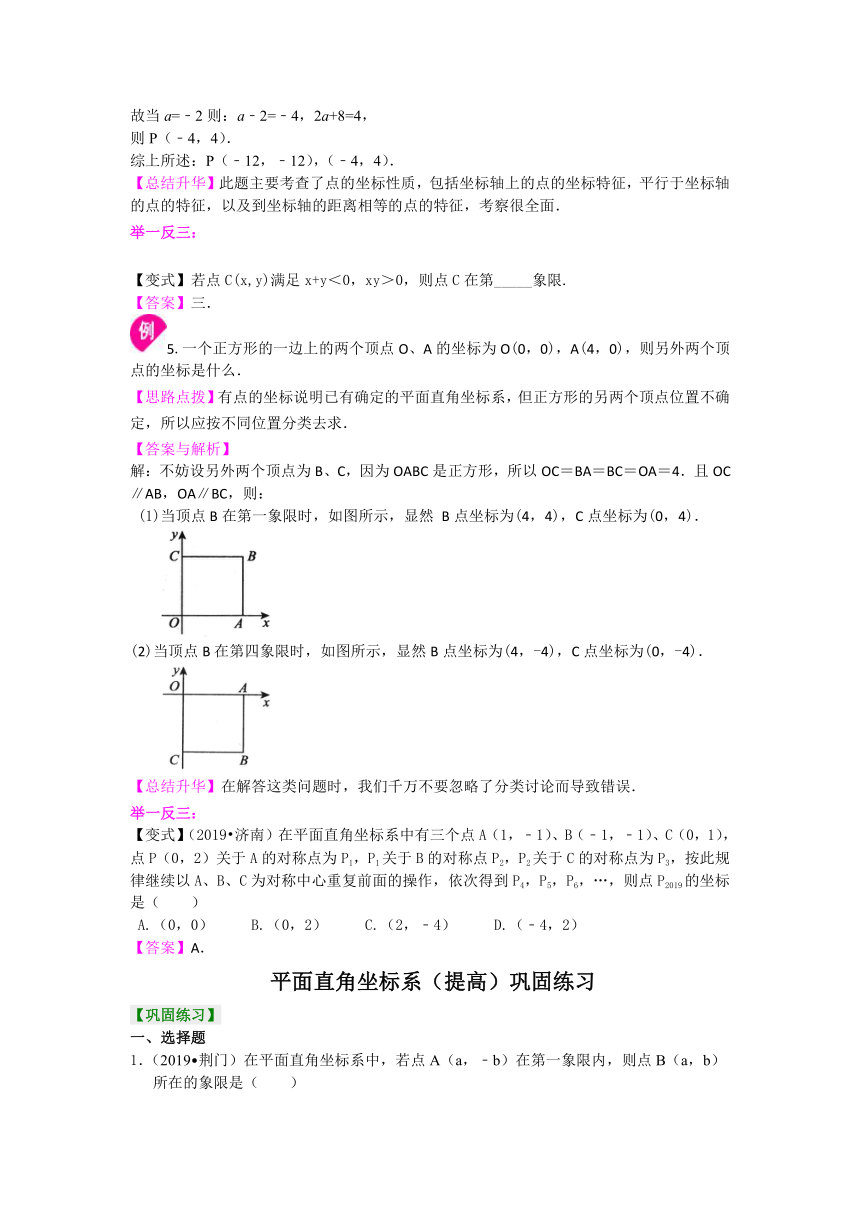
【变式】如图所示,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),……,则点A2008的坐标为________.
【答案】(-502,-502).
3.平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(-3,-1),B(1,3),C(2,-3).求△ABC的面积.
【思路点拨】三角形的三边都不与坐标轴平行,根据平面直角坐标系的特点,可以将三角形的面积转化为梯形或长方形的面积减去多余的直角三角形的面积,即可求得此三角形的面积.
【答案与解析】
解:如图所示,过点A、C分别作平行于y轴的直线与过B点平行于x轴的直线交于点D、E,则四边形ACED为梯形,根据点A(-3,-1)、B(1,3)、C(2,-3)可求得AD=4,CE=6,DB=4,BE=1,DE=5,所以△ABC的面积为:
.
【总结升华】点的坐标能体现点到坐标轴的距离,解决平面直角坐标系中的三角形面积问题,就是要充分利用这一点,将不规则图形转化为规则图形,再利用相关图形的面积计算公式求解.
类型三、坐标平面及点的特征
4. (2019春?沂水县期中)已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点Q的坐标为(1,5),直线PQ∥y轴;
(4)点P到x轴、y轴的距离相等.
【思路点拨】根据点的坐标特征一一求解.
【答案与解析】
解:(1)∵点P(a﹣2,2a+8),在x轴上,
∴2a+8=0,
解得:a=﹣4,
故a﹣2=﹣4﹣2=﹣6,
则P(﹣6,0);
(2))∵点P(a﹣2,2a+8),在y轴上,
∴a﹣2=0,
解得:a=2,
故2a+8=2×2+8=12,
则P(0,12);
(3)∵点Q的坐标为(1,5),直线PQ∥y轴;,
∴a﹣2=1,
解得:a=3,
故2a+8=14,
则P(1,14);
(4)∵点P到x轴、y轴的距离相等,
∴a﹣2=2a+8或a﹣2+2a+8=0,
解得:a1=﹣10,a2=﹣2,
故当a=﹣10则:a﹣2=﹣12,2a+8=﹣12,
则P(﹣12,﹣12);
故当a=﹣2则:a﹣2=﹣4,2a+8=4,
则P(﹣4,4).
综上所述:P(﹣12,﹣12),(﹣4,4).
【总结升华】此题主要考查了点的坐标性质,包括坐标轴上的点的坐标特征,平行于坐标轴的点的特征,以及到坐标轴的距离相等的点的特征,考察很全面.
举一反三:
【变式】若点C(x,y)满足x+y<0,xy>0,则点C在第_____象限.
【答案】三.
5.一个正方形的一边上的两个顶点O、A的坐标为O(0,0),A(4,0),则另外两个顶点的坐标是什么.
【思路点拨】有点的坐标说明已有确定的平面直角坐标系,但正方形的另两个顶点位置不确定,所以应按不同位置分类去求.
【答案与解析】
解:不妨设另外两个顶点为B、C,因为OABC是正方形,所以OC=BA=BC=OA=4.且OC∥AB,OA∥BC,则:
(1)当顶点B在第一象限时,如图所示,显然 B点坐标为(4,4),C点坐标为(0,4).
(2)当顶点B在第四象限时,如图所示,显然B点坐标为(4,-4),C点坐标为(0,-4).
【总结升华】在解答这类问题时,我们千万不要忽略了分类讨论而导致错误.
举一反三:
【变式】(2019?济南)在平面直角坐标系中有三个点A(1,﹣1)、B(﹣1,﹣1)、C(0,1),点P(0,2)关于A的对称点为P1,P1关于B的对称点P2,P2关于C的对称点为P3,按此规律继续以A、B、C为对称中心重复前面的操作,依次得到P4,P5,P6,…,则点P2019的坐标是( )
A.(0,0) B.(0,2) C.(2,﹣4) D.(﹣4,2)
【答案】A.
平面直角坐标系(提高)巩固练习
【巩固练习】
一、选择题
1.(2019?荆门)在平面直角坐标系中,若点A(a,﹣b)在第一象限内,则点B(a,b)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.点A(a,-2)在二、四象限的角平分线上,则a的值是( ).
A.2 B.-2 C. D.
3.已知点M到x轴、y轴的距离分别为4和6,且点M在x轴的上方、y轴的左侧,则点M的坐标为( ) .
A.(4,-6) B.(-4,6) C.(6,-4) D.(-6,4)
4.已知A(a,b)、B(b,a)表示同一个点,那么这个点一定在( ) .
A.第二、四象限的角平分线上 B.第一、三象限的角平分线上
C.平行于x轴的直线上 D.平行于y轴的直线上
5. 已知点,,过作轴于,并延长到,使,
且点坐标为,,则.
A.0 B.1 C.—1 D.—5
6. (2019春?鄂州校级期中)如图,一个粒子在第一象限和x,y轴的正半轴上运动,在第一秒内,它从原点运动到(0,1),接着它按图所示在x轴、y轴的平行方向来回运动,(即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→…)且每秒运动一个单位长度,那么2010秒时,这个粒子所处位置为( )
A.(14,44) B.(15,44) C.(44,14) D.(44,15)
二、填空题
7.(2019?黔南州)在平面直角坐标系中,对于平面内任一点(a,b),若规定以下三种变换:
①△(a,b)=(﹣a,b);
②○(a,b)=(﹣a,﹣b);
③Ω(a,b)=(a,﹣b),
按照以上变换例如:△(○(1,2))=(1,﹣2),则○(Ω(3,4))等于 .
8.线段AB的长度为3且平行x轴,已知点A的坐标为(2,-5),则点B的坐标为 .
9.如果点,,,,点在轴上,且的面积是5,则点坐标____.
10.设x、y为有理数,若|x+2y-2|+|2x-y+6|=0,则点(x,y)在第______象限.
11.(2019?华师一附中自主招生)如图,在一个单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2019的坐标为 .
12.在平面直角坐标系中,点A、B、C的坐标分别为:A(-2,1)、B(-3,-1),C(-1,-1),且D在x轴上方. 顺次连接这4个点得到的四边形是平行四边形, 则D点的坐标为_______.
三、解答题
13.如图,棋子“马”所处的位置为(2,3).
(1)你能表示图中“象”的位置吗?
(2)写出“马”的下一步可以到达的位置(象棋中“马”走“日”字或“”字)
14.如图,若B(x1,y1)、C(x2,y2)均为第一象限的点,O、B、C三点不在同一条直线上.
(1) 求△OBC的面积(用含x1、x2、y1、y2的代数式表示);
(2) 如图,若三个点的坐标分别为A(2,5),B(7,7),C(9,1),求四边形OABC的面积.
15.(2019春?西城区校级期中)在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“识别距离”,给出如下定义:
若|x1﹣x2|≥|y1﹣y2|,则点P1(x1,y1)与点P2(x2,y2)的“识别距离”为|x1﹣x2|;
若|x1﹣x2|<|y1﹣y2|,则P1(x1,y1)与点P2(x2,y2)的“识别距离”为|y1﹣y2|;
(1)已知点A(﹣1,0),B为y轴上的动点,
①若点A与B的“识别距离为”2,写出满足条件的B点的坐标 .
②直接写出点A与点B的“识别距离”的最小值 .
(2)已知C点坐标为C(m,m+3),D(0,1),求点C与D的“识别距离”的最小值及相应的C点坐标.
【答案与解析】
一、选择题
1. 【答案】D.
2. 【答案】A;
【解析】因为(a,-2)在二、四象限的角平分线上,所以a+(-2)=0,即a=2.
3. 【答案】D;
【解析】根据题意,画出下图,由图可知M(-6,4).
4. 【答案】B;
【解析】由题意可得:,横坐标等于纵坐标的点在一三象限的角平分线上.
5. 【答案】B;
【解析】由题意知: 点M(a,b)与点N(-2,-3)关于x轴对称,所以M(-2,3) .
6. 【答案】A.
【解析】解:设粒子运动到A1,A2,…An时所用的间分别为a1,a2,…,an,an﹣a1=2×n+…+2×3+2×2=2 (2+3+4+…+n),
an=n(n+1),44×45=1980,故运动了1980秒时它到点A44(44,44);
则运动了2010秒时,粒子所处的位置为(14,44).
故选A.
二、填空题
7. 【答案】(﹣3,4)
【解析】解:○(Ω(3,4))=○(3,﹣4)=(﹣3,4).故答案为:(﹣3,4).
8. 【答案】B(5,-5)或(-1,-5);
【解析】,而.
9. 【答案】(0,)或(0,);
【解析】,由的面积是5,可得的边AB上的高为,又点
C在y轴上,所以,.
10.【答案】二;
【解析】由绝对值的非负性,可得x,y的值,从而可得(x,y)所在的象限.
11.【答案】(1008,0).
【解析】解:∵A3是第一与第二个等腰直角三角形的公共点,
A5是第二与第三个等腰直角三角形的公共点,
A7是第三与第四个等腰直角三角形的公共点,
A9是第四与第五个等腰直角三角形的公共点,…,
∵2019=1006×2+1,
∴A2019是第1006个与第1007个等腰直角三角形的公共点,
∴A2019在x轴正半轴,
∵OA5=4,OA9=6,OA13=8,…,
∴OA2019=(2019+3)÷2=1008,
∴点A2019的坐标为(1008,0).
故答案为:(1008,0).
12.【答案】(0,1)或(-4,1);
【解析】,.
三、解答题
13.【解析】
解: (1)(5,3) ; (2)(1,1)、(3,1)、(4,2)、(1,5)、(4,4)、(3,5) .
14.【解析】
解: (1) 如图:
(2)连接OB,则:
四边形OABC的面积为:.
15.【解析】
解:(1)①(0,2)或(0,﹣2);
②“识别距离”的最小值是1;
(2)|m﹣0|=|m+3|,
解得m=8或,
当m=8时,“识别距离”为8,
当m=时,“识别距离”为,
所以,当m=时,“识别距离”最小值为,相应C(﹣,).
【学习目标】
1.理解平面直角坐标系概念,能正确画出平面直角坐标系.
2.能在平面直角坐标系中,根据坐标确定点,以及由点求出坐标,掌握点的坐标特征.
3.由数轴到平面直角坐标系,渗透类比的数学思想.
【典型例题】
类型一、有序数对表示位置
1.如图是小刚的一张笑脸,他对妹妹说:如果我用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成( ).
A.(1,0) B.(-1,0) C.(-1,1) D.(1,-1)
【思路点拨】由(0,2)表示左眼,用(2,2)表示右眼,可以确定平面直角坐标系中x轴与y轴的位置,从而可以确定嘴的位置.
【答案】A.
【解析】
解:根据(0,2)表示左眼,用(2,2)表示右眼, 可得嘴的坐标是(1,0), 故答案为A.
【总结升华】此题考查了坐标确定位置,由已知条件正确确定坐标轴的位置是解决本题的关键.
类型二、平面直角坐标系与点的坐标的概念
2.有一个长方形ABCD,长为5,宽为3,先建立一个平面直角坐标系,在此坐标系下求出A,B,C,D各点的坐标.
【答案与解析】
解:本题答案不唯一,现列举三种解法.
解法一:以点A为坐标原点,边AB所在的直线为x轴,边AD所在直线为y轴,建立平面直角坐标系,如图(1):
A(0,0),B(5,0), C(5,3), D (0,3).
解法二:以边AB的中点为坐标原点,边AB所在的直线为x轴,AB的中点和CD的中点所在的直线为y轴,建立平面直角坐标系,如图(2):
A(﹣2.5,0),B(2.5,0), C(2.5,3), D (-2.5,3).
解法三:以两组对边中点所在直线为x轴、y轴,建立平面直角坐标系,如图(3):
A(﹣2.5,-1.5),B(2.5,-1.5), C(2.5,1.5), D (-2.5,1.5).
【总结升华】在不同平面直角坐标系中,长方形顶点坐标不同,说明位置的相对性与绝对性,即只要原点、x轴和y轴确定,每一个点的位置也确定,而一旦原点或x轴、y轴改变,每一个点的位置也相对应地改变.
举一反三:
【变式】如图所示,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),……,则点A2008的坐标为________.
【答案】(-502,-502).
3.平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(-3,-1),B(1,3),C(2,-3).求△ABC的面积.
【思路点拨】三角形的三边都不与坐标轴平行,根据平面直角坐标系的特点,可以将三角形的面积转化为梯形或长方形的面积减去多余的直角三角形的面积,即可求得此三角形的面积.
【答案与解析】
解:如图所示,过点A、C分别作平行于y轴的直线与过B点平行于x轴的直线交于点D、E,则四边形ACED为梯形,根据点A(-3,-1)、B(1,3)、C(2,-3)可求得AD=4,CE=6,DB=4,BE=1,DE=5,所以△ABC的面积为:
.
【总结升华】点的坐标能体现点到坐标轴的距离,解决平面直角坐标系中的三角形面积问题,就是要充分利用这一点,将不规则图形转化为规则图形,再利用相关图形的面积计算公式求解.
类型三、坐标平面及点的特征
4. (2019春?沂水县期中)已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点Q的坐标为(1,5),直线PQ∥y轴;
(4)点P到x轴、y轴的距离相等.
【思路点拨】根据点的坐标特征一一求解.
【答案与解析】
解:(1)∵点P(a﹣2,2a+8),在x轴上,
∴2a+8=0,
解得:a=﹣4,
故a﹣2=﹣4﹣2=﹣6,
则P(﹣6,0);
(2))∵点P(a﹣2,2a+8),在y轴上,
∴a﹣2=0,
解得:a=2,
故2a+8=2×2+8=12,
则P(0,12);
(3)∵点Q的坐标为(1,5),直线PQ∥y轴;,
∴a﹣2=1,
解得:a=3,
故2a+8=14,
则P(1,14);
(4)∵点P到x轴、y轴的距离相等,
∴a﹣2=2a+8或a﹣2+2a+8=0,
解得:a1=﹣10,a2=﹣2,
故当a=﹣10则:a﹣2=﹣12,2a+8=﹣12,
则P(﹣12,﹣12);
故当a=﹣2则:a﹣2=﹣4,2a+8=4,
则P(﹣4,4).
综上所述:P(﹣12,﹣12),(﹣4,4).
【总结升华】此题主要考查了点的坐标性质,包括坐标轴上的点的坐标特征,平行于坐标轴的点的特征,以及到坐标轴的距离相等的点的特征,考察很全面.
举一反三:
【变式】若点C(x,y)满足x+y<0,xy>0,则点C在第_____象限.
【答案】三.
5.一个正方形的一边上的两个顶点O、A的坐标为O(0,0),A(4,0),则另外两个顶点的坐标是什么.
【思路点拨】有点的坐标说明已有确定的平面直角坐标系,但正方形的另两个顶点位置不确定,所以应按不同位置分类去求.
【答案与解析】
解:不妨设另外两个顶点为B、C,因为OABC是正方形,所以OC=BA=BC=OA=4.且OC∥AB,OA∥BC,则:
(1)当顶点B在第一象限时,如图所示,显然 B点坐标为(4,4),C点坐标为(0,4).
(2)当顶点B在第四象限时,如图所示,显然B点坐标为(4,-4),C点坐标为(0,-4).
【总结升华】在解答这类问题时,我们千万不要忽略了分类讨论而导致错误.
举一反三:
【变式】(2019?济南)在平面直角坐标系中有三个点A(1,﹣1)、B(﹣1,﹣1)、C(0,1),点P(0,2)关于A的对称点为P1,P1关于B的对称点P2,P2关于C的对称点为P3,按此规律继续以A、B、C为对称中心重复前面的操作,依次得到P4,P5,P6,…,则点P2019的坐标是( )
A.(0,0) B.(0,2) C.(2,﹣4) D.(﹣4,2)
【答案】A.
平面直角坐标系(提高)巩固练习
【巩固练习】
一、选择题
1.(2019?荆门)在平面直角坐标系中,若点A(a,﹣b)在第一象限内,则点B(a,b)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.点A(a,-2)在二、四象限的角平分线上,则a的值是( ).
A.2 B.-2 C. D.
3.已知点M到x轴、y轴的距离分别为4和6,且点M在x轴的上方、y轴的左侧,则点M的坐标为( ) .
A.(4,-6) B.(-4,6) C.(6,-4) D.(-6,4)
4.已知A(a,b)、B(b,a)表示同一个点,那么这个点一定在( ) .
A.第二、四象限的角平分线上 B.第一、三象限的角平分线上
C.平行于x轴的直线上 D.平行于y轴的直线上
5. 已知点,,过作轴于,并延长到,使,
且点坐标为,,则.
A.0 B.1 C.—1 D.—5
6. (2019春?鄂州校级期中)如图,一个粒子在第一象限和x,y轴的正半轴上运动,在第一秒内,它从原点运动到(0,1),接着它按图所示在x轴、y轴的平行方向来回运动,(即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→…)且每秒运动一个单位长度,那么2010秒时,这个粒子所处位置为( )
A.(14,44) B.(15,44) C.(44,14) D.(44,15)
二、填空题
7.(2019?黔南州)在平面直角坐标系中,对于平面内任一点(a,b),若规定以下三种变换:
①△(a,b)=(﹣a,b);
②○(a,b)=(﹣a,﹣b);
③Ω(a,b)=(a,﹣b),
按照以上变换例如:△(○(1,2))=(1,﹣2),则○(Ω(3,4))等于 .
8.线段AB的长度为3且平行x轴,已知点A的坐标为(2,-5),则点B的坐标为 .
9.如果点,,,,点在轴上,且的面积是5,则点坐标____.
10.设x、y为有理数,若|x+2y-2|+|2x-y+6|=0,则点(x,y)在第______象限.
11.(2019?华师一附中自主招生)如图,在一个单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2019的坐标为 .
12.在平面直角坐标系中,点A、B、C的坐标分别为:A(-2,1)、B(-3,-1),C(-1,-1),且D在x轴上方. 顺次连接这4个点得到的四边形是平行四边形, 则D点的坐标为_______.
三、解答题
13.如图,棋子“马”所处的位置为(2,3).
(1)你能表示图中“象”的位置吗?
(2)写出“马”的下一步可以到达的位置(象棋中“马”走“日”字或“”字)
14.如图,若B(x1,y1)、C(x2,y2)均为第一象限的点,O、B、C三点不在同一条直线上.
(1) 求△OBC的面积(用含x1、x2、y1、y2的代数式表示);
(2) 如图,若三个点的坐标分别为A(2,5),B(7,7),C(9,1),求四边形OABC的面积.
15.(2019春?西城区校级期中)在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“识别距离”,给出如下定义:
若|x1﹣x2|≥|y1﹣y2|,则点P1(x1,y1)与点P2(x2,y2)的“识别距离”为|x1﹣x2|;
若|x1﹣x2|<|y1﹣y2|,则P1(x1,y1)与点P2(x2,y2)的“识别距离”为|y1﹣y2|;
(1)已知点A(﹣1,0),B为y轴上的动点,
①若点A与B的“识别距离为”2,写出满足条件的B点的坐标 .
②直接写出点A与点B的“识别距离”的最小值 .
(2)已知C点坐标为C(m,m+3),D(0,1),求点C与D的“识别距离”的最小值及相应的C点坐标.
【答案与解析】
一、选择题
1. 【答案】D.
2. 【答案】A;
【解析】因为(a,-2)在二、四象限的角平分线上,所以a+(-2)=0,即a=2.
3. 【答案】D;
【解析】根据题意,画出下图,由图可知M(-6,4).
4. 【答案】B;
【解析】由题意可得:,横坐标等于纵坐标的点在一三象限的角平分线上.
5. 【答案】B;
【解析】由题意知: 点M(a,b)与点N(-2,-3)关于x轴对称,所以M(-2,3) .
6. 【答案】A.
【解析】解:设粒子运动到A1,A2,…An时所用的间分别为a1,a2,…,an,an﹣a1=2×n+…+2×3+2×2=2 (2+3+4+…+n),
an=n(n+1),44×45=1980,故运动了1980秒时它到点A44(44,44);
则运动了2010秒时,粒子所处的位置为(14,44).
故选A.
二、填空题
7. 【答案】(﹣3,4)
【解析】解:○(Ω(3,4))=○(3,﹣4)=(﹣3,4).故答案为:(﹣3,4).
8. 【答案】B(5,-5)或(-1,-5);
【解析】,而.
9. 【答案】(0,)或(0,);
【解析】,由的面积是5,可得的边AB上的高为,又点
C在y轴上,所以,.
10.【答案】二;
【解析】由绝对值的非负性,可得x,y的值,从而可得(x,y)所在的象限.
11.【答案】(1008,0).
【解析】解:∵A3是第一与第二个等腰直角三角形的公共点,
A5是第二与第三个等腰直角三角形的公共点,
A7是第三与第四个等腰直角三角形的公共点,
A9是第四与第五个等腰直角三角形的公共点,…,
∵2019=1006×2+1,
∴A2019是第1006个与第1007个等腰直角三角形的公共点,
∴A2019在x轴正半轴,
∵OA5=4,OA9=6,OA13=8,…,
∴OA2019=(2019+3)÷2=1008,
∴点A2019的坐标为(1008,0).
故答案为:(1008,0).
12.【答案】(0,1)或(-4,1);
【解析】,.
三、解答题
13.【解析】
解: (1)(5,3) ; (2)(1,1)、(3,1)、(4,2)、(1,5)、(4,4)、(3,5) .
14.【解析】
解: (1) 如图:
(2)连接OB,则:
四边形OABC的面积为:.
15.【解析】
解:(1)①(0,2)或(0,﹣2);
②“识别距离”的最小值是1;
(2)|m﹣0|=|m+3|,
解得m=8或,
当m=8时,“识别距离”为8,
当m=时,“识别距离”为,
所以,当m=时,“识别距离”最小值为,相应C(﹣,).
