沪科版数学八年级下册《第18章 勾股定理》单元测试卷及解析
文档属性
| 名称 | 沪科版数学八年级下册《第18章 勾股定理》单元测试卷及解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 98.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-06 12:29:57 | ||
图片预览

文档简介
沪科版数学八年级下册《第19章勾股定理》单元测试卷及解析
一、选择题(本大题共10小题,共50分)
下列各组数的三个数,可作为三边长构成直角三角形的是(????)
A. 1,2,3 B.
3
2
,
4
2
,
5
2
C.
1
3
,
1
4
,
1
5
D. 0.3,0.4,0.5
在????△??????中,斜边长????=3,??
??
2
+??
??
2
+??
??
2
的值为(????)
A. 18 B. 9 C. 6 D. 无法计算
在????△??????中,a,b,c为△??????三边长,则下列关系正确的是(????)
A.
??
2
+
??
2
=
??
2
B.
??
2
+
??
2
=
??
2
C.
??
2
+
??
2
=
??
2
D. 以上关系都有可能
△??????中∠??、∠??、∠??的对边分别是a、b、c,下列命题中的假命题是(????)
A. 如果∠???∠??=∠??,则△??????是直角三角形 B. 如果
??
2
=
??
2
?
??
2
,则△??????是直角三角形,且∠??=90° C. 如果(??+??)(?????)=
??
2
,则△??????是直角三角形 D. 如果∠??:∠??:∠??=5:2:3,则△??????是直角三角形
将直角三角形的三边都扩大相同的倍数后,得到的三角形一定是(????)
A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 以上三种情况都有可能
在△??????中,????=12????,????=9????,????=15????,下列关系成立的是(????)
A. ∠??+∠??>∠?? B. ∠??+∠??=∠?? C. ∠??+∠??<∠?? D. 以上都不对
小刚准备测量河水的深度,他把一根竹竿插到岸边1.5??远的河底,竹竿高出水面0.5??,把竹竿的顶端拉向岸边,竿顶和岸边的水平刚好相齐,河水的深度为(????)
A. 2m B. 2.5?? C. 2.25?? D. 3m
若一个三角形三边满足(??+??
)
2
?
??
2
=2????,则这个三角形是(????)
A. 直角三角形 B. 等腰直角三角形 C. 等腰三角形 D. 以上结论都不对
△??????中,????=15,????=13,高????=12,则△??????的周长为(????)
A. 42 B. 32 C. 42或32 D. 37或33
三角形的三边长分别是2??+1、2
??
2
+2??、2
??
2
+2??+1(??为自然数),则此三角形是(????)
A. 直角三角形 B. 等腰直角三角形 C. 等腰三角形 D. 无法判定
二、填空题(本大题共4小题,共20分)
已知a,b,c分别是????△??????的两条直角边长和斜边长,且??+??=14,??=10,则
??
△??????
= ______ .
如图,已知在????△??????中,∠??????=90°,????=4,分别以AC、BC为直径作半圆,面积分别记为
??
1
、
??
2
,则
??
1
+
??
2
等于______.
有一个长为12cm,宽为4cm,高为3cm的长方形铁盒,在其内部要放一根笔直的铅笔,则铅笔最长是______ .
如图,一圆柱高8cm,底面半径为
6
??
????,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是__________cm.
三、计算题(本大题共2小题,共20分)
如图,折叠长方形一边AD,点D落在BC边的点F处,????=10????,????=8????,求: (1)????的长; (2)????的长.
“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70????/?.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?(参考数据转换:1??/??=3.6????/?)
四、解答题(本大题共4小题,共60分)
如图,有一个长方形的场院ABCD,其中????=9??,????=12??,在B处竖直立着一根电线杆,在电线杆上距地面8m的E处有一盏电灯.点D到灯E的距离是多少?
学校校内有一块如图所示的三角形空地ABC,计划将这块空地建成一个花园,以美化校园环境,预计花园每平方米造价为30元,学校修建这个花园需要投资多少元?
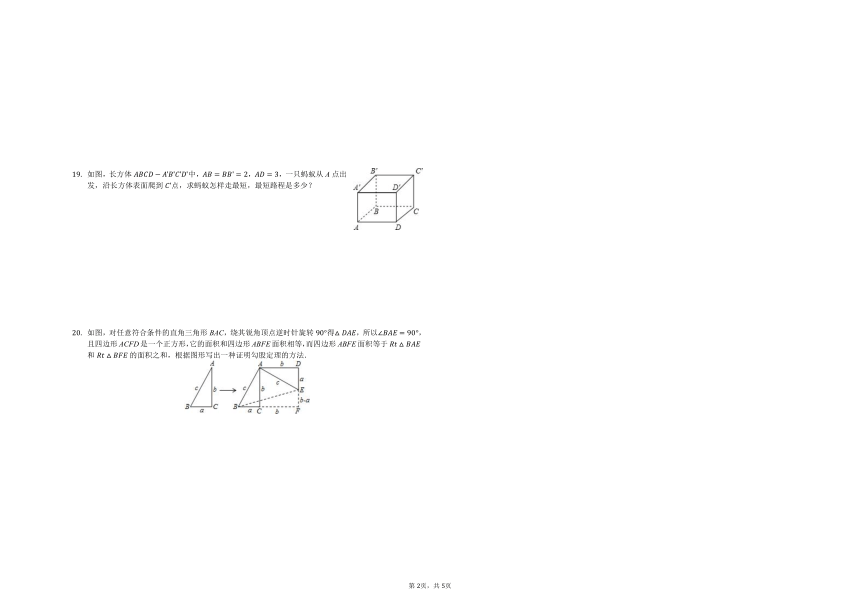
如图,长方体???????????′??′??′??′中,????=????′=2,????=3,一只蚂蚁从A点出发,沿长方体表面爬到??′点,求蚂蚁怎样走最短,最短路程是多少?
如图,对任意符合条件的直角三角形BAC,绕其锐角顶点逆时针旋转90°得△??????,所以∠??????=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于????△??????和????△??????的面积之和,根据图形写出一种证明勾股定理的方法.
答案和解析
1.【答案】D
【解析】解:∵
0.3
2
+
0.4
2
=0.25,
0.5
2
=0.25, ∴
0.3
2
+
0.4
2
=
0.5
2
, ∴0.3,0.4,0.5能构成直角三角形的三边. 故选D. 根据勾股定理的逆定理即可判断. 本题考查勾股定理的逆定理,解题的关键是记住勾股定理的逆定理的解题格式,属于中考常考题型. 2.【答案】A
【解析】解:∵????△??????中,BC为斜边, ∴??
??
2
+??
??
2
=??
??
2
, ∴??
??
2
+??
??
2
+??
??
2
=2??
??
2
=2×
3
2
=18. 故选A. 利用勾股定理将??
??
2
+??
??
2
转化为??
??
2
,再求值. 本题考查了勾股定理.正确判断直角三角形的直角边、斜边,利用勾股定理得出等式是解题的关键. 3.【答案】D
【解析】解:在????△??????中,a,b,c为△??????三边长, ∠??是直角,则有
??
2
+
??
2
=
??
2
; ∠??是直角,则有
??
2
+
??
2
=
??
2
; ∠??是直角,则有
??
2
+
??
2
=
??
2
. 故选:D. 根据勾股定理,分∠??是直角,∠??是直角,∠??是直角,三种情况讨论可得a,b,c之间的关系. 考查了勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方. 4.【答案】B
【解析】解:A、根据三角形内角和定理,可求出角C为90度,故正确; B、解得应为∠??=90度,故错误; C、化简后有
??
2
=
??
2
+
??
2
,根据勾股定理,则△??????是直角三角形,故正确; D、设三角分别为5x,3x,2x,根据三角形内角和定理可求得三外角分别为:90度,36度,54度,则△??????是直角三角形,故正确. 故选:B. 直角三角形的判定方法有:①求得一个角为90°,②利用勾股定理的逆定理. 本题考查了直角三角形的判定. 5.【答案】A
【解析】解:根据题意,新三角形与原三角形对应边成比例, 所以两三角形相似, 所以得到的三角形是直角三角形. 故选A. 根据“直角三角形的三边都扩大相同的倍数”得到新三角形与原三角形相似,所以是直角三角形. 此题考查了相似三角形的判定: ①有两个对应角相等的三角形相似; ②有两个对应边的比相等,且其夹角相等,则两个三角形相似; ③三组对应边的比相等,则两个三角形相似. 6.【答案】B
【解析】解:因为
12
2
+
9
2
=
15
2
,所以三角形是直角三角形,则∠??+∠??=∠??.故选B. 根据勾股定理的逆定理进行分析,从而得到三角形的形状,则不难求得其各角的关系. 本题考查了直角三角形的判定及勾股定理逆定理的应用. 7.【答案】A
【解析】解:如图,若假设竹竿长x米,则水深(???0.5)米,由题意得,
??
2
=
1.5
2
+(???0.5
)
2
, 解得.??=2.5. 所以水深2.5?0.5=2(米). 故选:A. 经分析知:可以放到一个直角三角形中计算.此直角三角形的斜边是竹竿的长,设为x米.一条直角边是1.5,另一条直角边是(???0.5)米.根据勾股定理,得:
??
2
=
1.5
2
+(???0.5
)
2
,求出x的值,即可得出答案. 此题考查了勾股定理的应用,解题的难点在于能够理解题意,正确画出图形. 8.【答案】A
【解析】解:∵(??+??
)
2
?
??
2
=2????, ∴
??
2
+
??
2
+2?????
??
2
=2????, ∴
??
2
+
??
2
=
??
2
, ∴这个三角形为直角三角形. 故选:A. 化简等式,可得
??
2
+
??
2
=
??
2
,由勾股定理逆定理,进而可得其为直角三角形. 本题考查了勾股定理逆定理的运用,是基础知识比较简单. 9.【答案】C
【解析】解:此题应分两种情况说明: (1)当△??????为锐角三角形时,在????△??????中, ????=
??
??
2
???
??
2
=
15
2
??
12
2
?
=9, 在????△??????中, ????=
??
??
2
???
??
2
=
13
2
??
12
2
=5 ∴????=5+9=14 ∴△??????的周长为:15+13+14=42; (2)当△??????为钝角三角形时, 在????△??????中,????=
??
??
2
???
??
2
=
15
2
??
12
2
?
=9, 在????△??????中,????=
??
??
2
???
??
2
=
13
2
??
12
2
=5, ∴????=9?5=4. ∴△??????的周长为:15+13+4=32 ∴当△??????为锐角三角形时,△??????的周长为42;当△??????为钝角三角形时,△??????的周长为32. 故选:C. 本题应分两种情况进行讨论: (1)当△??????为锐角三角形时,在????△??????和????△??????中,运用勾股定理可将BD和CD的长求出,两者相加即为BC的长,从而可将△??????的周长求出; (2)当△??????为钝角三角形时,在????△??????和????△??????中,运用勾股定理可将BD和CD的长求出,两者相减即为BC的长,从而可将△??????的周长求出. 此题考查了勾股定理及解直角三角形的知识,在解本题时应分两种情况进行讨论,易错点在于漏解,同学们思考问题一定要全面,有一定难度. 10.【答案】A
【解析】解:∵(2
??
2
+2??
)
2
+(2??+1
)
2
=4
??
4
+4
??
2
+8
??
3
+4
??
2
+4??+1 =4
??
4
+8
??
3
+8
??
2
+4??+1; (2
??
2
+2??+1
)
2
=(2
??
2
+2??+1)(2
??
2
+2??+1) =4
??
4
+4
??
3
+2
??
2
+4
??
3
+4
??
2
+2??+2
??
2
+2??+1 =4
??
4
+8
??
3
+8
??
2
+4??+1; ∴(2
??
2
+2??
)
2
+(2??+1
)
2
=(2
??
2
+2??+1
)
2
, ∴三角形是直角三角形. 故选A. 欲求证是否为直角三角形,这里给出三角形三边的长,只要验证两小边的平方和等于最长边的平方即可. 本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可. 勾股定理的逆定理:若三角形三边满足
??
2
+
??
2
=
??
2
,那么这个三角形是直角三角形. 11.【答案】24
【解析】解:∵??,b,c分别是????△??????的两条直角边长和斜边长,且??+??=14,??=10, ∴??=14???,则(14???
)
2
+
??
2
=
??
2
, 故(14???
)
2
+
??
2
=
10
2
, 解得:
??
1
=6,
??
2
=8, 则
??
1
=8,
??
2
=6, 即
??
△??????
=
1
2
????=
1
2
×6×8=24. 故答案为:24. 直接利用勾股定理结合已知得出关于b的等式,进而求出答案. 此题主要考查了勾股定理以及三角形面积求法,正确得出直角边长是解题关键. 12.【答案】2??
【解析】解:
??
1
=
1
2
??(
????
2
)
2
=
1
8
????
??
2
,
??
2
=
1
8
????
??
2
, 所以
??
1
+
??
2
=
1
8
??(??
??
2
+??
??
2
)=
1
8
????
??
2
=2??. 故答案为:2??. 根据半圆面积公式结合勾股定理,知
??
1
+
??
2
等于以斜边为直径的半圆面积. 此题根据半圆的面积公式以及勾股定理证明:以直角三角形的两条直角边为直径的半圆面积和等于以斜边为直径的半圆面积,重在验证勾股定理. 13.【答案】13cm
【解析】解:铅笔的长为
12
2
+
4
2
+
3
2
=
144+16+9
=13????. 故答案为:13cm. 本题根据题目中所给的信息,可以构造出直角三角形,再利用勾股定理解答即可. 本题考查正确运用勾股定理.善于观察题目的信息是解题以及学好数学的关键. 14.【答案】10
【解析】【分析】 此题主要考查了立体图形的展开和两点之间线段最短,解题的关键是根据题意画出展开图,表示出各线段的长度. 此题最直接的解法,就是将圆柱展开,然后利用两点之间线段最短解答. 【解答】 解:底面圆周长为2????,底面半圆弧长为????,即半圆弧长为:
1
2
×2??×
6
??
=6(????),展开得: ∵????=8????,????=6????, 根据勾股定理得:????=
8
2
+
6
2
=10(????). 故答案为:10. 15.【答案】解:(1)由题意可得,????=????=10????, 在????△??????中,∵????=8, ∴????=6????, ∴????=?????????=10?6=4????. (2)由题意可得????=????,可设DE的长为x, 则在????△??????中, (8???
)
2
+
4
2
=
??
2
, 解得??=5, 即EF的长为5cm.
【解析】(1)由于△??????翻折得到△??????,所以可得????=????,则在????△??????中,第一问可求解; (2)由于????=????,可设EF的长为x,进而在????△??????中,利用勾股定理求解直角三角形即可. 本题主要考查了矩形的性质以及翻折的问题,能够熟练运用矩形的性质求解一些简答的问题. 16.【答案】解:在????△??????中,????=30??,????=50??; 据勾股定理可得: ????=
??
??
2
???
??
2
=
50
2
?
30
2
=40(??) ∴小汽车的速度为??=
40
2
=20(??/??)=20×3.6(????/?)=72(????/?); ∵72(????/?)>70(????/?); ∴这辆小汽车超速行驶. 答:这辆小汽车超速了.
【解析】本题求小汽车是否超速,其实就是求BC的距离,直角三角形ABC中,有斜边AB的长,有直角边AC的长,那么BC的长就很容易求得,根据小汽车用2s行驶的路程为BC,那么可求出小汽车的速度,然后再判断是否超速了. 本题是将实际问题转化为直角三角形中的数学问题,可把条件和问题放到直角三角形中,进行解决.要注意题目中单位的统一. 17.【答案】解:在????△??????中,∠??????=90°,????=
??
??
2
+??
??
2
=
9
2
+
12
2
=15米, 在????△??????中,∠??????=90°,????=
??
??
2
+??
??
2
=
8
2
+
15
2
=17米. 故点D到灯E的距离是17米.
【解析】在????△??????中求出BD,然后在????△??????中利用勾股定理即可得出DE的长度. 本题考查了勾股定理的应用,属于基础题,解答本题的关键是熟练掌握勾股定理的表达式. 18.【答案】解:过点A作????⊥????于点D,设????=??,则????=14???, 在????△??????与????△??????中, ∵??
??
2
=??
??
2
???
??
2
,??
??
2
=??
??
2
???
??
2
, ∴??
??
2
???
??
2
=??
??
2
???
??
2
,即
13
2
?
??
2
=
15
2
?(14???
)
2
,解得??=5, ∴??
??
2
=??
??
2
???
??
2
=
13
2
?
5
2
=144, ∴????=12(米), ∴学校修建这个花园的费用=30×
1
2
×14×12=2520(元). 答:学校修建这个花园需要投资2520元.
【解析】过点A作????⊥????于点D,设????=??,则????=14???,再根据勾股定理求出x的值,进而可得出AD的长,由三角形的面积公式即可得出结论. 本题考查的是勾股定理的应用及三角形的面积公式,根据题意作出辅助线,构造出直角三角形是解答此题的关键. 19.【答案】解:如图1所示: 由题意得:????=3,????′=2+2=4, 在????△??????′中,由勾股定理得????′=
??
??
2
+????
′
2
=
3
2
+
4
2
=5, 如图2所示: 由题意得:????=5,??′??=2, 在????△??????′中,由勾股定理得;????′=
??
??
2
+????
′
2
=
5
2
+
2
2
=
29
, ∵
29
>5. ∴第一种方法蚂蚁爬行的路线最短,最短路程是5.
【解析】做此题要把这个长方体中,蚂蚁所走的路线放到一个平面内,由于在平面内线段最短,根据勾股定理即可计算. 本题考查了平面展开?最短路径问题,此题的关键是明确线段最短这一知识点,然后把立体的长方体放到一个平面内,求出最短的路线. 20.【答案】解:由图可得: 正方形ACFD的面积=四边形ABFE的面积=????△??????和????△??????的面积之和, 即
??
正方形????????
=
??
△??????
+
??
△??????
, ∴
??
2
=
1
2
??
2
+
(??+??)(?????)
2
, 整理得:
??
2
+
??
2
=
??
2
.
【解析】证明勾股定理时,用几个全等的直角三角形拼成一个规则的图形,然后利用四边形ABFE面积等于????△??????和????△??????的面积之和,化简整理得到勾股定理. 本题主要考查了勾股定理的证明,勾股定理的证明方法有很多种,一般采用拼图的方法证明.在解题时注意:先利用拼图的方法拼图,然后再利用面积相等,证明勾股定理.
