新人教版九年级下数学27.2.1相似三角形的判定(1)课件(50张PPT)
文档属性
| 名称 | 新人教版九年级下数学27.2.1相似三角形的判定(1)课件(50张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-06 20:38:16 | ||
图片预览


文档简介
(共50张PPT)
人教版义务教育教科书
数学九年级下册
第二十七章 相似 ppt
A
B
C
D
E
F
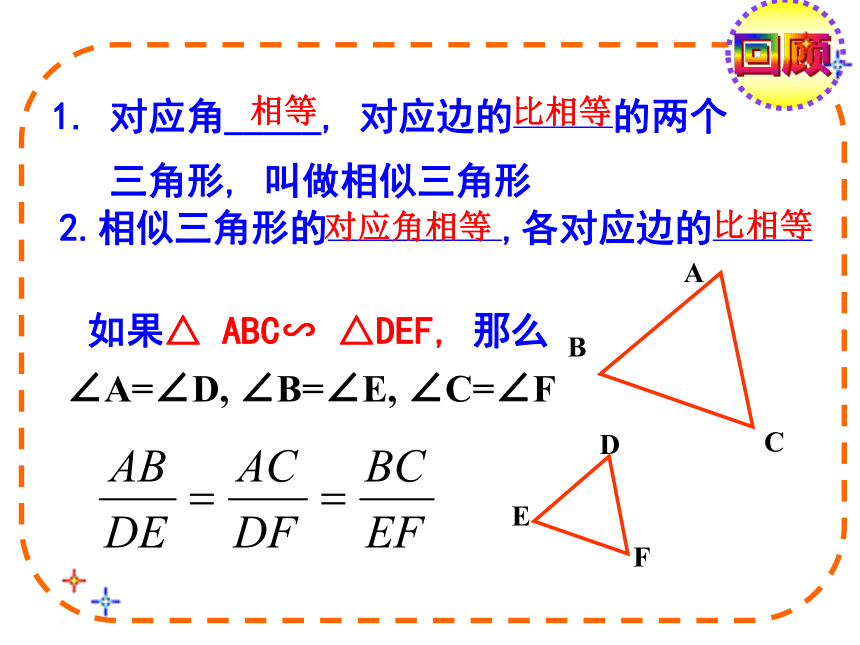
1. 对应角_____, 对应边的————的两个
三角形, 叫做相似三角形
相等
比相等
2.相似三角形的———————,各对应边的————
对应角相等
比相等
如果△ ABC∽ △DEF, 那么
∠A=∠D, ∠B=∠E, ∠C=∠F
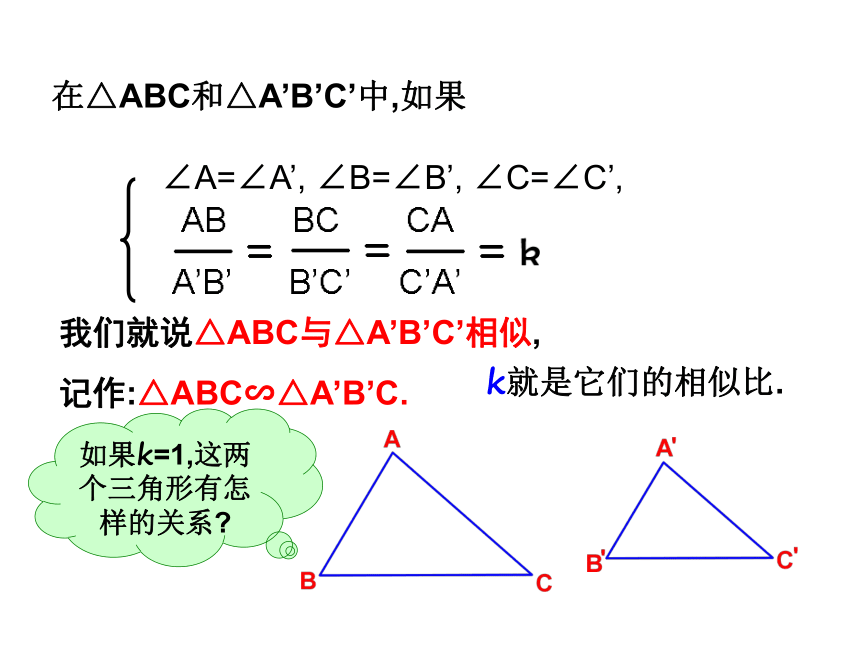
在△ABC和△A’B’C’中,如果
∠A=∠A’, ∠B=∠B’, ∠C=∠C’,
我们就说△ABC与△A’B’C’相似,
记作:△ABC∽△A’B’C.
k就是它们的相似比.
如果k=1,这两个三角形有怎样的关系
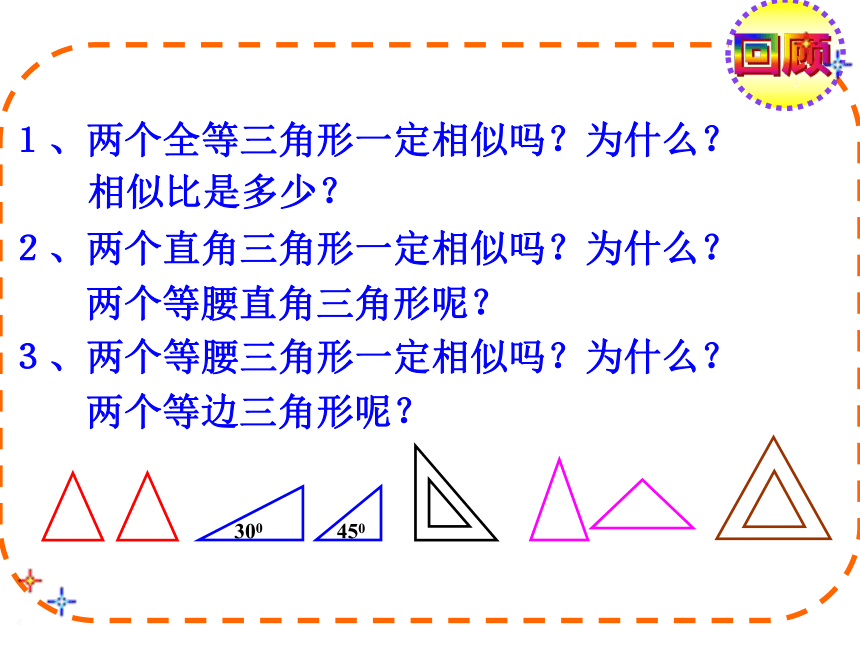
1、两个全等三角形一定相似吗?为什么?
2、两个直角三角形一定相似吗?为什么?
两个等腰直角三角形呢?
3、两个等腰三角形一定相似吗?为什么?
两个等边三角形呢?
相似比是多少?
300
450
学习三角形全等时,我们知道,除了可以通过证明对应角相等,对应边相等来判定两个三角形全等外,还有判定的简便方法(SSS,SAS,ASA,AAS).类似地,判定两个三角形相似时,是不是对所有的对应角和对应边都要一一验证呢?
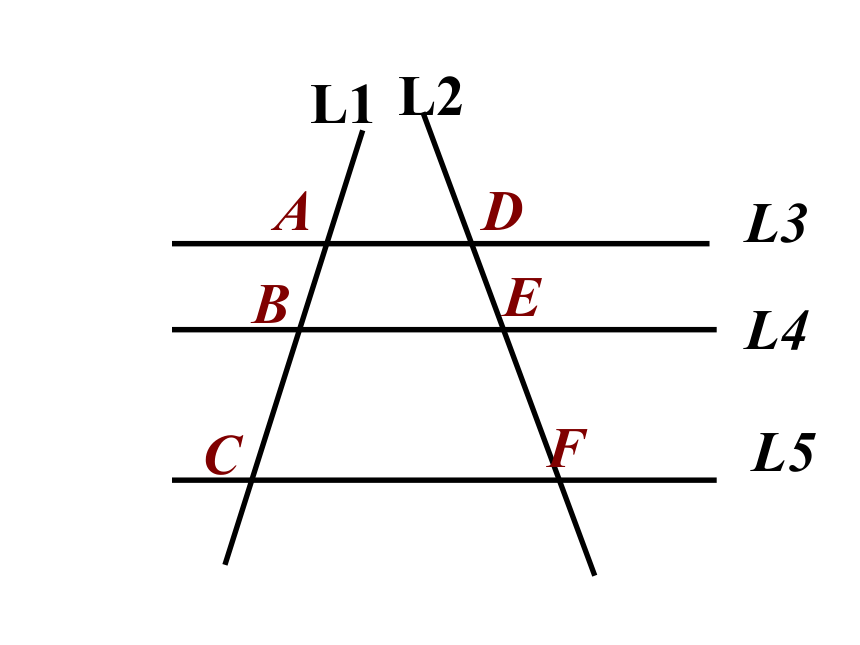
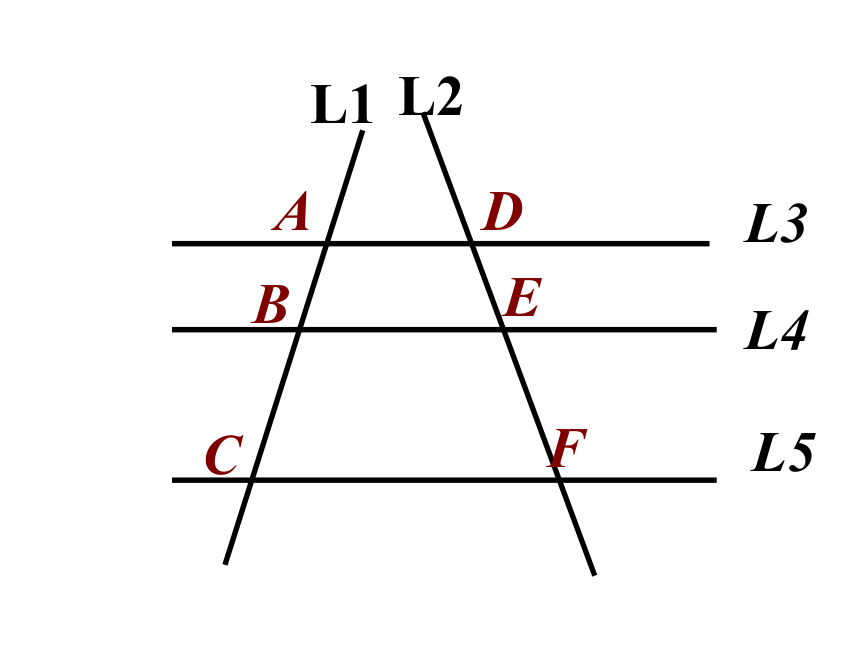
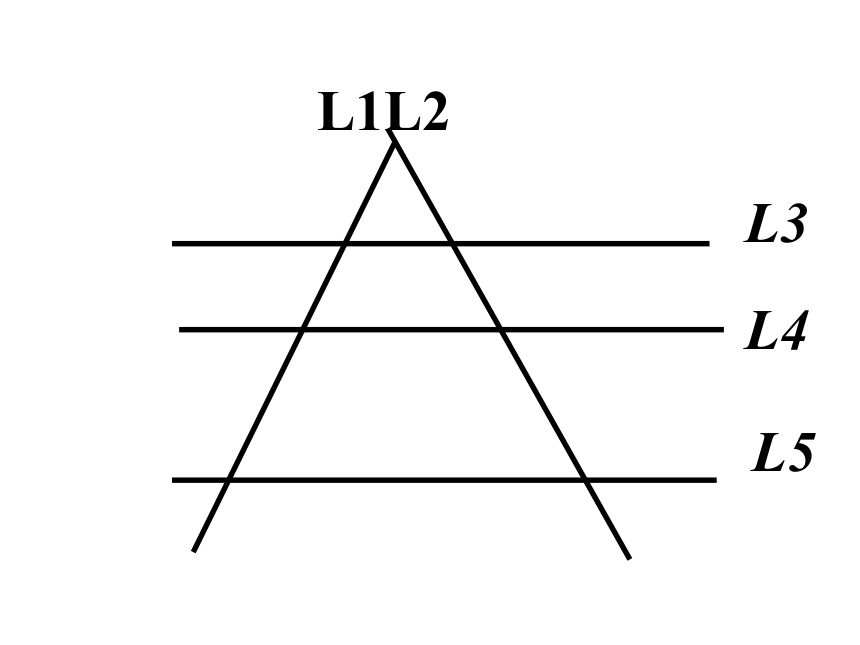
为了证明相似三角形的判定定理,我们先来学习下面的平行线分线段成比例定理。
L3
L4
L5
A
B
C
D
E
F
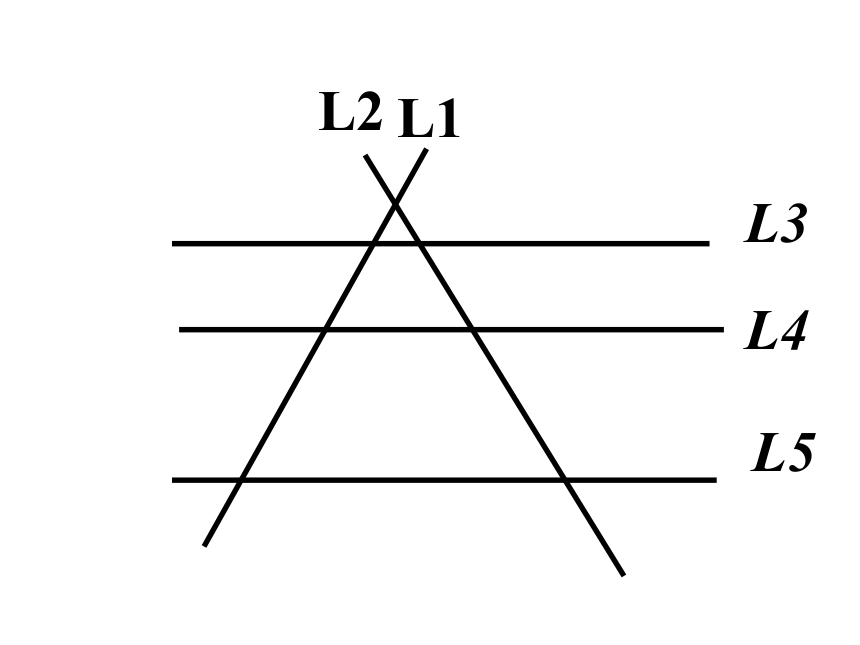
L1
L2
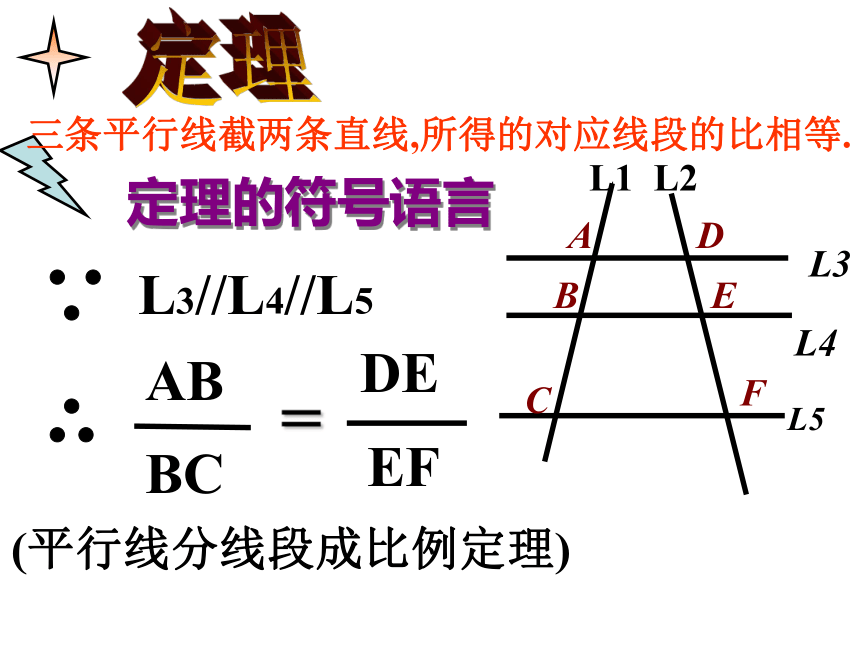
定理的符号语言
L3//L4//L5
=
AB
DE
BC
EF
(平行线分线段成比例定理)
三条平行线截两条直线,所得的对应线段的比相等.
D
E
F
A
B
C
L3
L4
L5
L1
L2
L3
L4
L5
A
B
C
D
E
F
L1
L2
L3
L4
L5
L1
L2
L3
L4
L5
L1L2
L3
L4
L5
L1
L2
L3
L4
L5
L1
L2
L3
L4
L5
L1
L2
L3
L4
L5
L1
L2
L1
L2
L3
L4
L5
L1
L2
L3
L4
L5
L1
L2
L3
L4
L5
A
B
C
E
D
A
B
C
D
E
∵ DE∥BC
AD
AE
AC
AB
=
∵
∵ DE∥BC
AD
AE
AC
AB
=
∵
数学符号语言
数学符号语言
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段的比相等
A
B
C
D
E
——
——
练习一:
1、判断题:
如图:DE∥BC, 下列各式是否正确
D:
——
——
=
AD
AE
AB
AC
( )
C:
——
——
=
AD
AC
AE
AB
( )
B:
——
——
=
AD
BD
AE
CE
( )
A:
AD
AB
=
AE
AC
( )
A
B
C
E
D
2、填空题:
如图:DE∥BC,
已知:
2
=
——
AE
AC
—
5
=
——
AD
AB
求:
——
2
—
5
A
B
C
D
E
已知:DE//BC, AB=15,AC=9,
BD=4 . 求:AE=
例题2
解:
∵ DE∥BC
AB AC
BD CE
∴
——
——
=
(推论)
15 9
4 CE
——
——
=
即
=
12
5
—
∴
CE
12
2
5
5
∴
AE= AC+CE=9+ =11—
—
练习二:
A
B
D
C
E
EC
BC
DC
——
——
=
A
B
C
D
E
(A组)
(B组)
1、如图: 已知 DE∥BC,
AB = 14, AC = 18 ,
AE = 10,
求:AD的长。
2、如图: 已知AB⊥BD,
ED⊥BD,垂足分别为
B、D。
求证:
AC
CB = 4,
BE
AB
=
A
A
B
C
D
E
C
达标检测题:
1、如图: 已知 DE∥BC,
AB = 5, AC = 7 ,
AD= 2,
求:AE的长。
B
D
E
(A组)
(B组)
2、已知 ∠A =∠E=60°
求:BD的长。
——
—
2
3
如图,在△ABC 中,DE//BC,
DE分别交AB,AC 于点D,E,
△ADE与△ABC有什么关系
思
考
?
直觉告诉我们, △ADE与△ABC相似,我们通过相似的定义证明这个结论.
先证明两个三角形的对应角相等.
在△ADE与△ABC中, ∠A=∠A,
∵DE//BC,
∴∠ADE=∠B, ∠AED=∠C.
再证明两个三角形的对应边的比相等.
过E作EF//AB,EF交BC于F点.
在平行四边形BFED中,DE=BF,DB=EF.
即:△ADE与△ABC中,
∠A=∠A,∠ADE=∠B, ∠AED=∠C.
∴△ADE∽△ABC
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
平行于三角形一边的直线与其它两边相交,所得的三角形与原三角形________.
相似
“A”型
A
B
C
D
E
(图1)
请写出它们的对应边的比例式
已知:如图,AB∥EF ∥CD,
3
图中共有____对相似三角形。
△EOF∽△COD
AB∥EF
△AOB∽ △FOE
AB∥CD
EF∥CD
△AOB ∽△DOC
如图,△ABC 中,DE∥BC,GF∥AB,DE、GF交于点O,则图中与△ABC相似的三角形共有多少个 请你写出来.
解: 与△ABC相似的三角形有3个:
△ADE
△GFC
△GOE
A
B
C
D
E
F
G
O
如图在平行四边形ABCD中,E为AD上一点,连结CE并延长交BA的延长线于点F,
请找出相似的三角形并表示出来。
如图,已知DE ∥ BC,AE=50cm,EC=30cm,BC=70cm,
∠BAC=450,∠ACB=400.
(1)求∠AED和∠ADE的大小;(2)求DE的长.
(2)
A
D
B
E
C
解: (1)
DE ∥ BC
△ADE∽△ABC
∠AED=∠C=400.
△ADE∽△ABC
在△ADE中, ∠ADE=1800-400-450=950.
如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_____。
A
B
C
D
E
F
G
H
I
△ADG∽△AEH∽△AFI∽△ABC
1:4
类似于判定三角形全等的方法,我们还能不能通过三边来判断两个三角形相似呢?
是否有△ABC∽△A’B’C’?
A
B
C
C’
B’
A’
三边对应成 比例
已知:如图△ABC和△ 中,
求证:△ABC∽△A`B`C`
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,
A`
B`
C`
A
B
C
D
E
过点D作DE∥BC交AC于点E.
又
∴ △ADE∽△ABC , ∴
∵
∴ .
因此 .
∴△ ∽△ABC
∴△ADE≌△
要证明△ABC∽△A’B’C’,可以先作一个与△ABC全等的三角形,证明它△A’B’C’与相似.这里所作的三角形是证明的中介,它把△ABC△A’B’C’联系起来.
A
B
C
C’
B’
A’
△ABC∽△A’B’C’
如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
简单地说:三边对应的比相等,两三角形相似.
类似于判定三角形全等的方法,我们能通过两边和夹角来判断两个三角形相似呢?
实际上,我们有利用两边和夹角判定两个三角形相似的方法.
如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角相似.
思
考
?
对于△ABC和△A’B’C’, 如果 ,
∠B=∠B’,这两个三角形一定相似吗 试着画画看.
例1:根据下列条件,判断△ABC与△A’B’C’是否相似,并说明理由.
(1)∠A=1200,AB=7cm,AC=14cm.
∠A’=1200,A’B’=3cm,A’C’=6cm.
(2)AB=4 cm,BC=6cm,AC=8cm,
A’B’=12cm,B’C’=18cm,A’C’=21cm.
△ABC与△A’B’C‘的三组对应边的比不等,它们不相似.
∽
要使两三角形相似,不改变的AC长,A’C’的长应改为多少?
1.根据下列条件,判断△ABC与△A’B’C’是否相似,并说明理由:
(1)∠A=400,AB=8,AC=15, ∠A’=400,A’B’=16,A’C’=30;
(2)AB=10cm,BC=8cm,AC=16cm,
A’B’=16cm,B’C’=12.8cm,A’C’=25.6cm.
2.图中的两个三角形是否相似
试说明∠BAD=∠CAE.
A
D
C
E
B
∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC━∠DAC=∠DAE━∠DAC
即∠BAD=∠CAE
答案是2:1
4:2=5:x=6:y
4:x=5:2=6:y
4:x=5:y=6:2
要作两个形状相同的三角形框架,其中一个三角形的三边的长分别为4、5、6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似
4
5
6
2
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似;
两边对应成比例且夹角相等,两三角形相似.
相似三角形的判定方法
三边对应成比例,两三角形相似.
作业
《高效课堂》课时作业6—14
人教版义务教育教科书
数学九年级下册
第二十七章 相似 ppt
A
B
C
D
E
F
1. 对应角_____, 对应边的————的两个
三角形, 叫做相似三角形
相等
比相等
2.相似三角形的———————,各对应边的————
对应角相等
比相等
如果△ ABC∽ △DEF, 那么
∠A=∠D, ∠B=∠E, ∠C=∠F
在△ABC和△A’B’C’中,如果
∠A=∠A’, ∠B=∠B’, ∠C=∠C’,
我们就说△ABC与△A’B’C’相似,
记作:△ABC∽△A’B’C.
k就是它们的相似比.
如果k=1,这两个三角形有怎样的关系
1、两个全等三角形一定相似吗?为什么?
2、两个直角三角形一定相似吗?为什么?
两个等腰直角三角形呢?
3、两个等腰三角形一定相似吗?为什么?
两个等边三角形呢?
相似比是多少?
300
450
学习三角形全等时,我们知道,除了可以通过证明对应角相等,对应边相等来判定两个三角形全等外,还有判定的简便方法(SSS,SAS,ASA,AAS).类似地,判定两个三角形相似时,是不是对所有的对应角和对应边都要一一验证呢?
为了证明相似三角形的判定定理,我们先来学习下面的平行线分线段成比例定理。
L3
L4
L5
A
B
C
D
E
F
L1
L2
定理的符号语言
L3//L4//L5
=
AB
DE
BC
EF
(平行线分线段成比例定理)
三条平行线截两条直线,所得的对应线段的比相等.
D
E
F
A
B
C
L3
L4
L5
L1
L2
L3
L4
L5
A
B
C
D
E
F
L1
L2
L3
L4
L5
L1
L2
L3
L4
L5
L1L2
L3
L4
L5
L1
L2
L3
L4
L5
L1
L2
L3
L4
L5
L1
L2
L3
L4
L5
L1
L2
L1
L2
L3
L4
L5
L1
L2
L3
L4
L5
L1
L2
L3
L4
L5
A
B
C
E
D
A
B
C
D
E
∵ DE∥BC
AD
AE
AC
AB
=
∵
∵ DE∥BC
AD
AE
AC
AB
=
∵
数学符号语言
数学符号语言
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段的比相等
A
B
C
D
E
——
——
练习一:
1、判断题:
如图:DE∥BC, 下列各式是否正确
D:
——
——
=
AD
AE
AB
AC
( )
C:
——
——
=
AD
AC
AE
AB
( )
B:
——
——
=
AD
BD
AE
CE
( )
A:
AD
AB
=
AE
AC
( )
A
B
C
E
D
2、填空题:
如图:DE∥BC,
已知:
2
=
——
AE
AC
—
5
=
——
AD
AB
求:
——
2
—
5
A
B
C
D
E
已知:DE//BC, AB=15,AC=9,
BD=4 . 求:AE=
例题2
解:
∵ DE∥BC
AB AC
BD CE
∴
——
——
=
(推论)
15 9
4 CE
——
——
=
即
=
12
5
—
∴
CE
12
2
5
5
∴
AE= AC+CE=9+ =11—
—
练习二:
A
B
D
C
E
EC
BC
DC
——
——
=
A
B
C
D
E
(A组)
(B组)
1、如图: 已知 DE∥BC,
AB = 14, AC = 18 ,
AE = 10,
求:AD的长。
2、如图: 已知AB⊥BD,
ED⊥BD,垂足分别为
B、D。
求证:
AC
CB = 4,
BE
AB
=
A
A
B
C
D
E
C
达标检测题:
1、如图: 已知 DE∥BC,
AB = 5, AC = 7 ,
AD= 2,
求:AE的长。
B
D
E
(A组)
(B组)
2、已知 ∠A =∠E=60°
求:BD的长。
——
—
2
3
如图,在△ABC 中,DE//BC,
DE分别交AB,AC 于点D,E,
△ADE与△ABC有什么关系
思
考
?
直觉告诉我们, △ADE与△ABC相似,我们通过相似的定义证明这个结论.
先证明两个三角形的对应角相等.
在△ADE与△ABC中, ∠A=∠A,
∵DE//BC,
∴∠ADE=∠B, ∠AED=∠C.
再证明两个三角形的对应边的比相等.
过E作EF//AB,EF交BC于F点.
在平行四边形BFED中,DE=BF,DB=EF.
即:△ADE与△ABC中,
∠A=∠A,∠ADE=∠B, ∠AED=∠C.
∴△ADE∽△ABC
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
平行于三角形一边的直线与其它两边相交,所得的三角形与原三角形________.
相似
“A”型
A
B
C
D
E
(图1)
请写出它们的对应边的比例式
已知:如图,AB∥EF ∥CD,
3
图中共有____对相似三角形。
△EOF∽△COD
AB∥EF
△AOB∽ △FOE
AB∥CD
EF∥CD
△AOB ∽△DOC
如图,△ABC 中,DE∥BC,GF∥AB,DE、GF交于点O,则图中与△ABC相似的三角形共有多少个 请你写出来.
解: 与△ABC相似的三角形有3个:
△ADE
△GFC
△GOE
A
B
C
D
E
F
G
O
如图在平行四边形ABCD中,E为AD上一点,连结CE并延长交BA的延长线于点F,
请找出相似的三角形并表示出来。
如图,已知DE ∥ BC,AE=50cm,EC=30cm,BC=70cm,
∠BAC=450,∠ACB=400.
(1)求∠AED和∠ADE的大小;(2)求DE的长.
(2)
A
D
B
E
C
解: (1)
DE ∥ BC
△ADE∽△ABC
∠AED=∠C=400.
△ADE∽△ABC
在△ADE中, ∠ADE=1800-400-450=950.
如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_____。
A
B
C
D
E
F
G
H
I
△ADG∽△AEH∽△AFI∽△ABC
1:4
类似于判定三角形全等的方法,我们还能不能通过三边来判断两个三角形相似呢?
是否有△ABC∽△A’B’C’?
A
B
C
C’
B’
A’
三边对应成 比例
已知:如图△ABC和△ 中,
求证:△ABC∽△A`B`C`
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,
A`
B`
C`
A
B
C
D
E
过点D作DE∥BC交AC于点E.
又
∴ △ADE∽△ABC , ∴
∵
∴ .
因此 .
∴△ ∽△ABC
∴△ADE≌△
要证明△ABC∽△A’B’C’,可以先作一个与△ABC全等的三角形,证明它△A’B’C’与相似.这里所作的三角形是证明的中介,它把△ABC△A’B’C’联系起来.
A
B
C
C’
B’
A’
△ABC∽△A’B’C’
如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
简单地说:三边对应的比相等,两三角形相似.
类似于判定三角形全等的方法,我们能通过两边和夹角来判断两个三角形相似呢?
实际上,我们有利用两边和夹角判定两个三角形相似的方法.
如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角相似.
思
考
?
对于△ABC和△A’B’C’, 如果 ,
∠B=∠B’,这两个三角形一定相似吗 试着画画看.
例1:根据下列条件,判断△ABC与△A’B’C’是否相似,并说明理由.
(1)∠A=1200,AB=7cm,AC=14cm.
∠A’=1200,A’B’=3cm,A’C’=6cm.
(2)AB=4 cm,BC=6cm,AC=8cm,
A’B’=12cm,B’C’=18cm,A’C’=21cm.
△ABC与△A’B’C‘的三组对应边的比不等,它们不相似.
∽
要使两三角形相似,不改变的AC长,A’C’的长应改为多少?
1.根据下列条件,判断△ABC与△A’B’C’是否相似,并说明理由:
(1)∠A=400,AB=8,AC=15, ∠A’=400,A’B’=16,A’C’=30;
(2)AB=10cm,BC=8cm,AC=16cm,
A’B’=16cm,B’C’=12.8cm,A’C’=25.6cm.
2.图中的两个三角形是否相似
试说明∠BAD=∠CAE.
A
D
C
E
B
∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC━∠DAC=∠DAE━∠DAC
即∠BAD=∠CAE
答案是2:1
4:2=5:x=6:y
4:x=5:2=6:y
4:x=5:y=6:2
要作两个形状相同的三角形框架,其中一个三角形的三边的长分别为4、5、6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似
4
5
6
2
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似;
两边对应成比例且夹角相等,两三角形相似.
相似三角形的判定方法
三边对应成比例,两三角形相似.
作业
《高效课堂》课时作业6—14
