新人教版九年级下册数学27.2.1相似三角形的判定课件(边边边 15张PPT)
文档属性
| 名称 | 新人教版九年级下册数学27.2.1相似三角形的判定课件(边边边 15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 98.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-06 15:47:09 | ||
图片预览

文档简介
课件15张PPT。相似三角形的判定
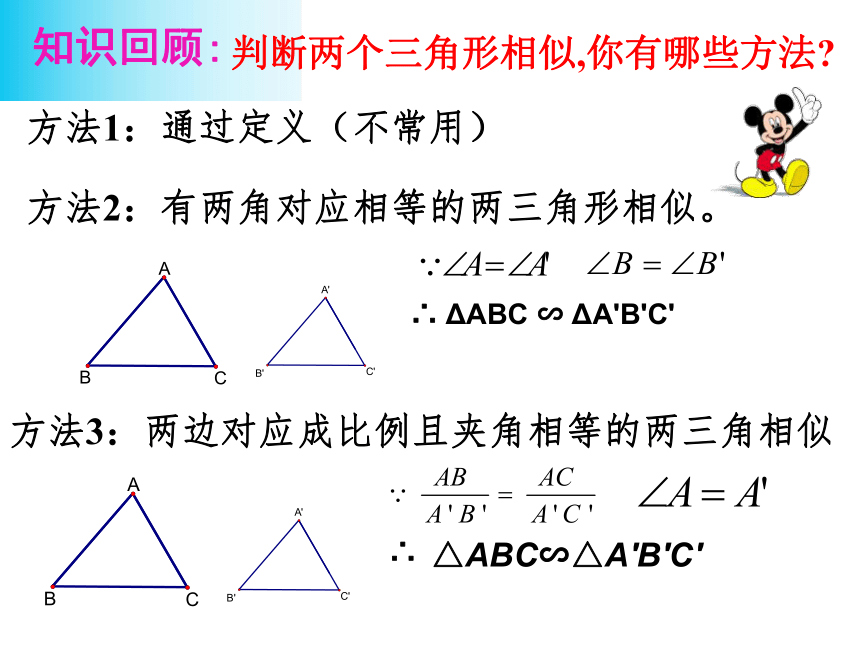
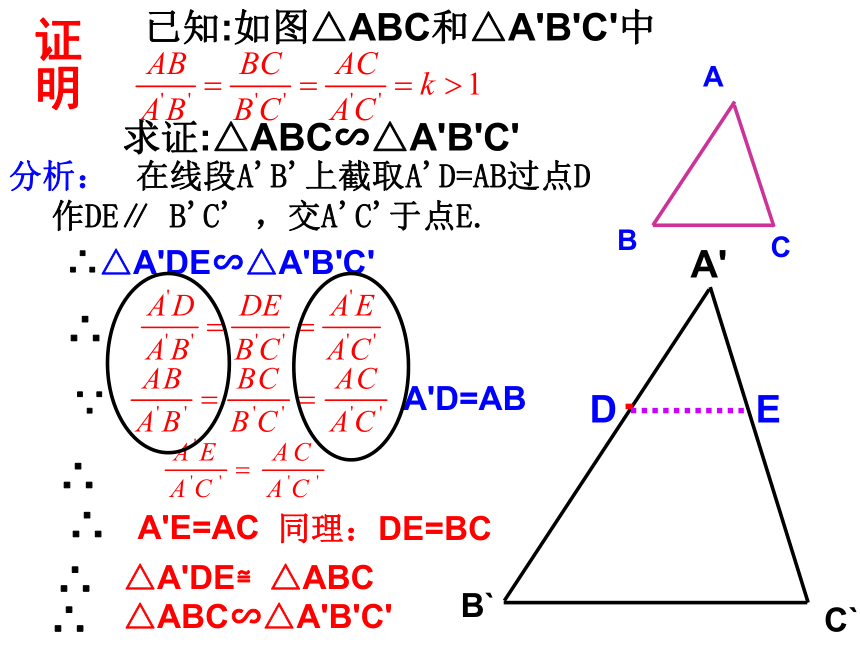
———边边边方法1:通过定义(不常用)方法2:有两角对应相等的两三角形相似。方法3:两边对应成比例且夹角相等的两三角相似∴ ΔABC ∽ ΔA'B'C' 在线段A'B'上截取A'D=AB过点D作DE∥ B'C' ,交A'C'于点E. 已知:如图△ABC和△A'B'C'中
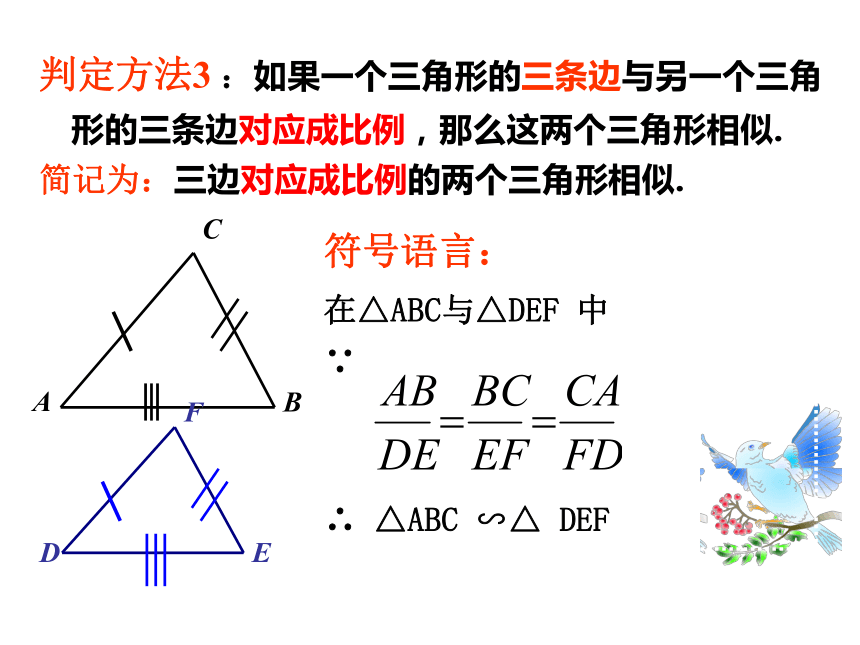
求证:△ABC∽△A'B'C'DE分析:∴△A'DE∽△A'B'C'A'D=AB同理:DE=BCA'E=AC△A'DE≌△ABC△ABC∽△A'B'C'∴∴∴∴证明判定方法3 :如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.
简记为:三边对应成比例的两个三角形相似.符号语言:
在△ABC与△DEF 中
∵
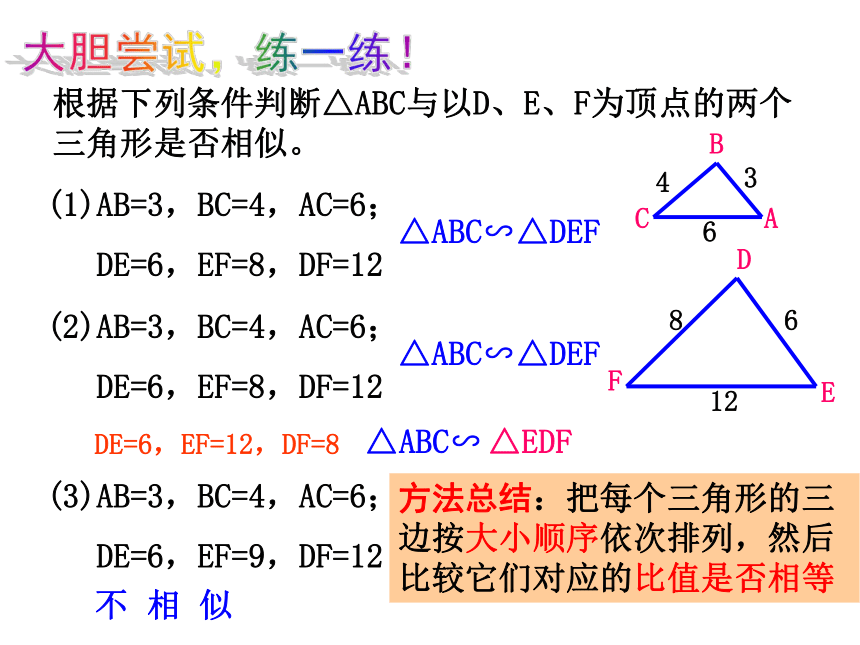
∴ △ABC ∽△ DEF根据下列条件判断△ABC与以D、E、F为顶点的两个三角形是否相似。(1)AB=3,BC=4,AC=6;
DE=6,EF=8,DF=12(3)AB=3,BC=4,AC=6;
DE=6,EF=9,DF=12(2)AB=3,BC=4,AC=6;
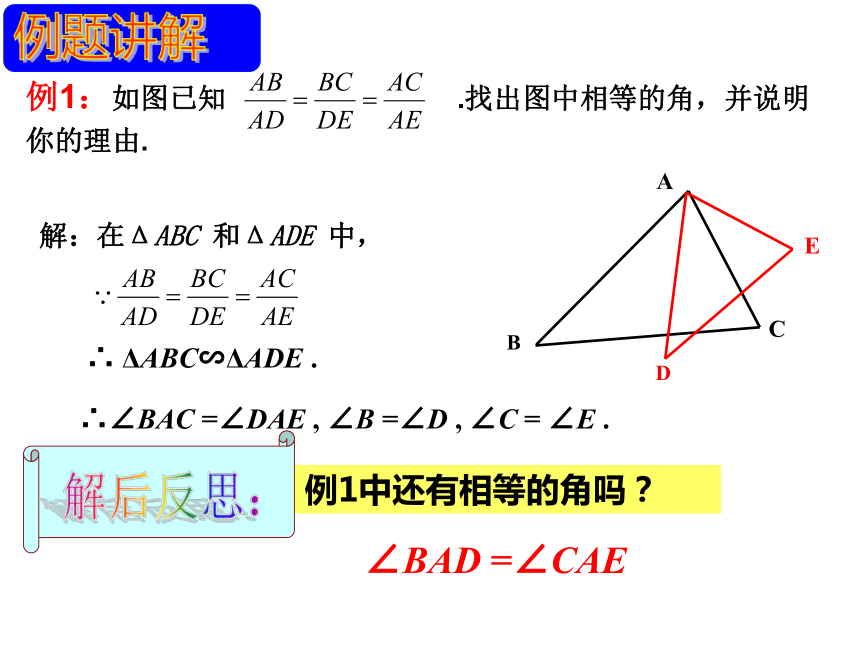
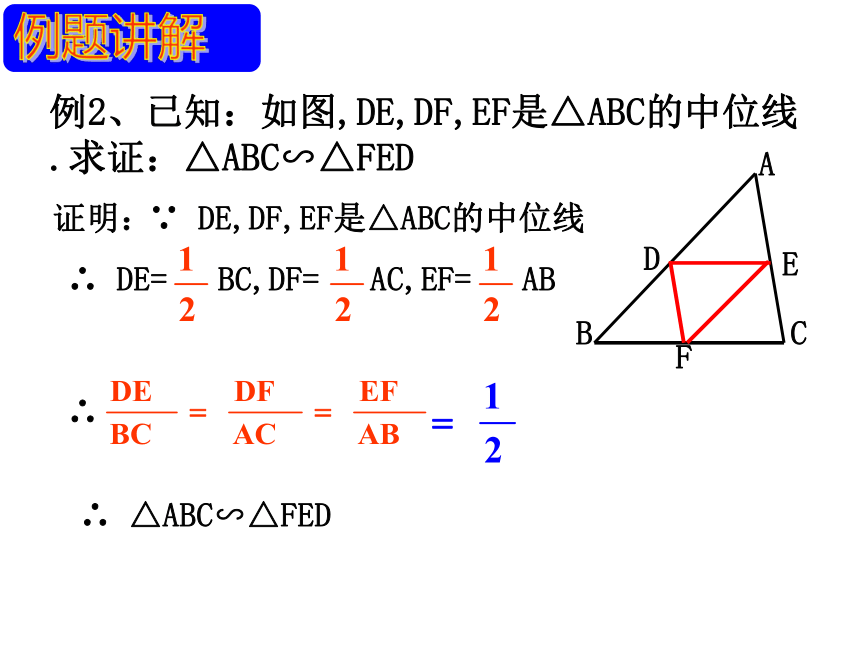
DE=6,EF=8,DF=12△ABC∽△DEF△ABC∽不 相 似△EDFDE=6,EF=12,DF=8△ABC∽△DEF大胆尝试,练一练!方法总结:把每个三角形的三边按大小顺序依次排列,然后比较它们对应的比值是否相等例1:如图已知 .找出图中相等的角,并说明 你的理由. 解:在ΔABC 和ΔADE 中,∴ ΔABC∽ΔADE .∴∠BAC =∠DAE , ∠B =∠D , ∠C = ∠E .∠BAD =∠CAE例2、已知:如图,DE,DF,EF是△ABC的中位线.求证:△ABC∽△FED证明:∵ DE,DF,EF是△ABC的中位线∴ DE= BC,DF= AC,EF= AB∴ △ABC∽△FED 如图,某地四个乡镇A、B、C、D之间建有公路,已知AB=14千米,AD=28千米, BD=21千米, BC=42千米,DC=31.5千米,公路AB与CD平行吗?说出你的理由。1428214231.5解:公路AB与CD平行。∴ △ABD∽△BDC .∴ ∠ABD=∠BDC . ∴ AB∥DC .例3:2.如图,在4×4的正方形方格中,△ABC和△DEF
的顶点都在边长为1的小正方形的顶点上.判断△ABC与△DEF是否相似,并证明你的结论.3.∠APD=90°,AP=PB=BC=CD 下列结论正确的是( ) A. △PAB∽△PCA B.△PAB∽△PDA C.△ABC∽△DBA D. △ABC∽△DCAC1.如图:在△ABC中,D,E分别为AB,AC上的点,若AD=4,BD=3.5,AE=5,EC=1,下列结论错误的是( )A.1.5DE=BC B.△ABC∽△AED
C.∠ADE=∠B D.∠AED=∠BDEA C2.在△ABC中,AB=9,AC=12,BC=18,
D为AC上的一点,DC=8,在AB上取
一点E,得到△ADE,若图中两个三
角形相似时,则DE长为_____仔细动脑想一想3、在直角梯形BACD中,AC⊥CD,AC=CD=4AB, E是AC中点.求证:△ABE∽△CED变式练习:若AB=2,E是线段AC上的一个动点, △ABE与△CED相似,求AE的长.理解4:2=5:x=6:y
4:x=5:2=6:y
4:x=5:y=6:2要作两个形状相同的三角形框架,其中一个三角形的三边的长分别为4、5、6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似?4562(1)定义法:对应角相等、对应边成比例;
(2)预备定理:平行于三角形一边的直线截其他两边所在的直线,截得的三角形和原三角形相似;
(3) 判定定理:(常用的方法)
1.两角对应相等的两个三角形相似
2.两边对应成比例且夹角相等的两个三角形相似
3.三边对应成比例,两个三角形相似课堂小结
.判定三角形相似的方法有:1. 如图,在正方形ABCD中,已知P是BC上的点,且BP=3PC,Q是CD的中点,试判断△ADQ∽△QCP吗?说明理由.这是探索结论的题型,要先观察,猜测思考题:思考题:2.如图所示,在平面直角坐标系中,已知AO=12cm,OB=6cm,点P从点O开始沿OA边向点A以1cm/s的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动.如果P,Q同时出发,用t(s)表示移动的时间(0≤t≤6),那么:
(1)设△POQ的面积为y,求y关于t的函数解析式;
(2)当△POQ的面积最大时,将△POQ沿直线PQ翻折后得到△PCQ,试判断点C是否落在直线AB上,并说明理由;
(3)当t为何值是,△POQ与△AOB相似?
———边边边方法1:通过定义(不常用)方法2:有两角对应相等的两三角形相似。方法3:两边对应成比例且夹角相等的两三角相似∴ ΔABC ∽ ΔA'B'C' 在线段A'B'上截取A'D=AB过点D作DE∥ B'C' ,交A'C'于点E. 已知:如图△ABC和△A'B'C'中
求证:△ABC∽△A'B'C'DE分析:∴△A'DE∽△A'B'C'A'D=AB同理:DE=BCA'E=AC△A'DE≌△ABC△ABC∽△A'B'C'∴∴∴∴证明判定方法3 :如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.
简记为:三边对应成比例的两个三角形相似.符号语言:
在△ABC与△DEF 中
∵
∴ △ABC ∽△ DEF根据下列条件判断△ABC与以D、E、F为顶点的两个三角形是否相似。(1)AB=3,BC=4,AC=6;
DE=6,EF=8,DF=12(3)AB=3,BC=4,AC=6;
DE=6,EF=9,DF=12(2)AB=3,BC=4,AC=6;
DE=6,EF=8,DF=12△ABC∽△DEF△ABC∽不 相 似△EDFDE=6,EF=12,DF=8△ABC∽△DEF大胆尝试,练一练!方法总结:把每个三角形的三边按大小顺序依次排列,然后比较它们对应的比值是否相等例1:如图已知 .找出图中相等的角,并说明 你的理由. 解:在ΔABC 和ΔADE 中,∴ ΔABC∽ΔADE .∴∠BAC =∠DAE , ∠B =∠D , ∠C = ∠E .∠BAD =∠CAE例2、已知:如图,DE,DF,EF是△ABC的中位线.求证:△ABC∽△FED证明:∵ DE,DF,EF是△ABC的中位线∴ DE= BC,DF= AC,EF= AB∴ △ABC∽△FED 如图,某地四个乡镇A、B、C、D之间建有公路,已知AB=14千米,AD=28千米, BD=21千米, BC=42千米,DC=31.5千米,公路AB与CD平行吗?说出你的理由。1428214231.5解:公路AB与CD平行。∴ △ABD∽△BDC .∴ ∠ABD=∠BDC . ∴ AB∥DC .例3:2.如图,在4×4的正方形方格中,△ABC和△DEF
的顶点都在边长为1的小正方形的顶点上.判断△ABC与△DEF是否相似,并证明你的结论.3.∠APD=90°,AP=PB=BC=CD 下列结论正确的是( ) A. △PAB∽△PCA B.△PAB∽△PDA C.△ABC∽△DBA D. △ABC∽△DCAC1.如图:在△ABC中,D,E分别为AB,AC上的点,若AD=4,BD=3.5,AE=5,EC=1,下列结论错误的是( )A.1.5DE=BC B.△ABC∽△AED
C.∠ADE=∠B D.∠AED=∠BDEA C2.在△ABC中,AB=9,AC=12,BC=18,
D为AC上的一点,DC=8,在AB上取
一点E,得到△ADE,若图中两个三
角形相似时,则DE长为_____仔细动脑想一想3、在直角梯形BACD中,AC⊥CD,AC=CD=4AB, E是AC中点.求证:△ABE∽△CED变式练习:若AB=2,E是线段AC上的一个动点, △ABE与△CED相似,求AE的长.理解4:2=5:x=6:y
4:x=5:2=6:y
4:x=5:y=6:2要作两个形状相同的三角形框架,其中一个三角形的三边的长分别为4、5、6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似?4562(1)定义法:对应角相等、对应边成比例;
(2)预备定理:平行于三角形一边的直线截其他两边所在的直线,截得的三角形和原三角形相似;
(3) 判定定理:(常用的方法)
1.两角对应相等的两个三角形相似
2.两边对应成比例且夹角相等的两个三角形相似
3.三边对应成比例,两个三角形相似课堂小结
.判定三角形相似的方法有:1. 如图,在正方形ABCD中,已知P是BC上的点,且BP=3PC,Q是CD的中点,试判断△ADQ∽△QCP吗?说明理由.这是探索结论的题型,要先观察,猜测思考题:思考题:2.如图所示,在平面直角坐标系中,已知AO=12cm,OB=6cm,点P从点O开始沿OA边向点A以1cm/s的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动.如果P,Q同时出发,用t(s)表示移动的时间(0≤t≤6),那么:
(1)设△POQ的面积为y,求y关于t的函数解析式;
(2)当△POQ的面积最大时,将△POQ沿直线PQ翻折后得到△PCQ,试判断点C是否落在直线AB上,并说明理由;
(3)当t为何值是,△POQ与△AOB相似?
