新人教版九年级下数学27.2.1相似三角形的判定复习课课件(47张ppt)
文档属性
| 名称 | 新人教版九年级下数学27.2.1相似三角形的判定复习课课件(47张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 955.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-06 20:47:46 | ||
图片预览



文档简介
课件47张PPT。相似三角形的判定复 习 课 你学习了哪些判定两个三角形相似的方法?两直角三角形相似还有 ?
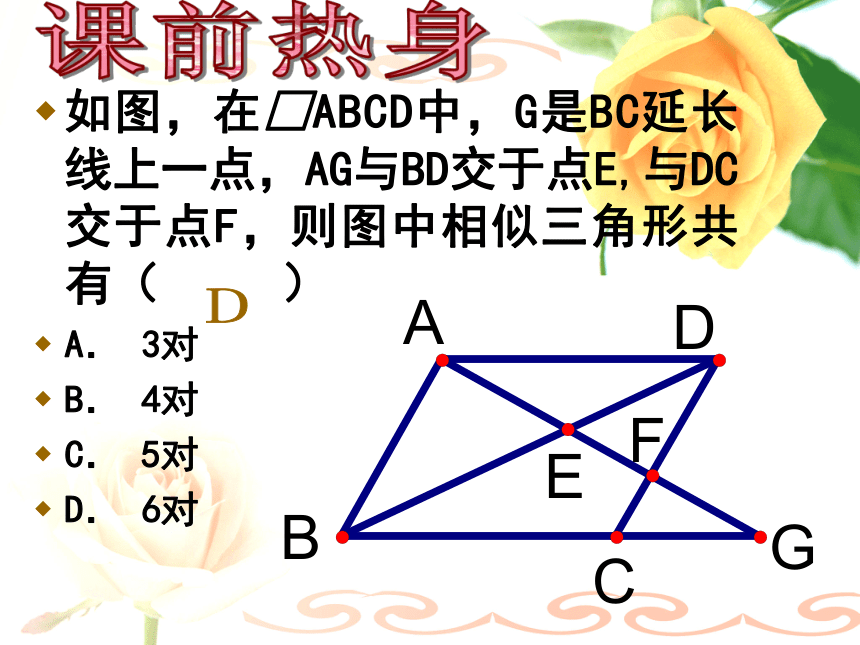
相似知识盘点对应角相等,对应边成比例。2.预备定理:3.判定定理1:4.判定定理2:5.判定定理3:1.定义:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。两角对应相等,两三角形相似。两边对应成比例且夹角相等, 两三角形相似。三边对应成比例,两三角形相似。6.直角三角形相似的判定定理: 斜边和一条直角边对应成比例,两直角三角形相似 如图,在□ABCD中,G是BC延长线上一点,AG与BD交于点E,与DC交于点F,则图中相似三角形共有( )
A. 3对
B. 4对
C. 5对
D. 6对
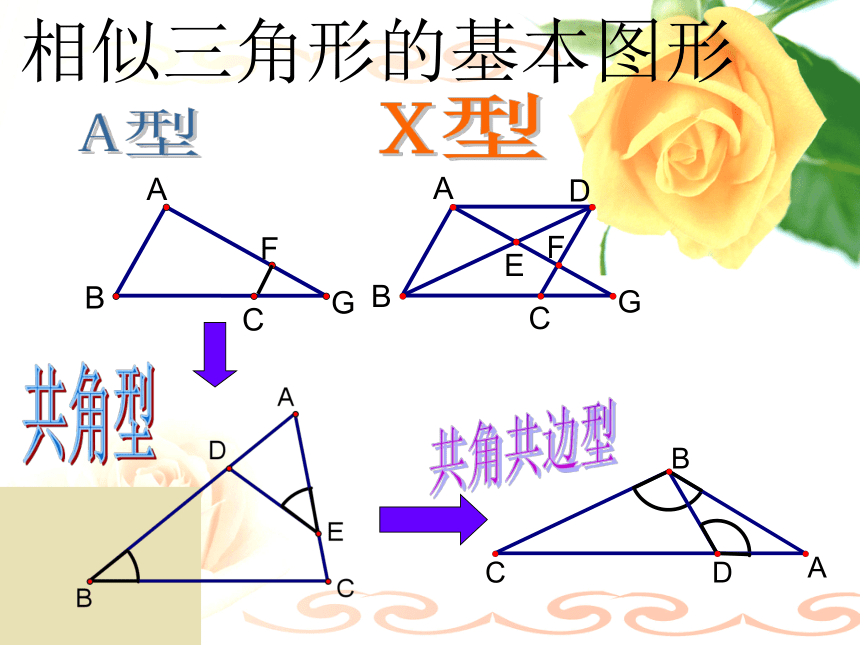
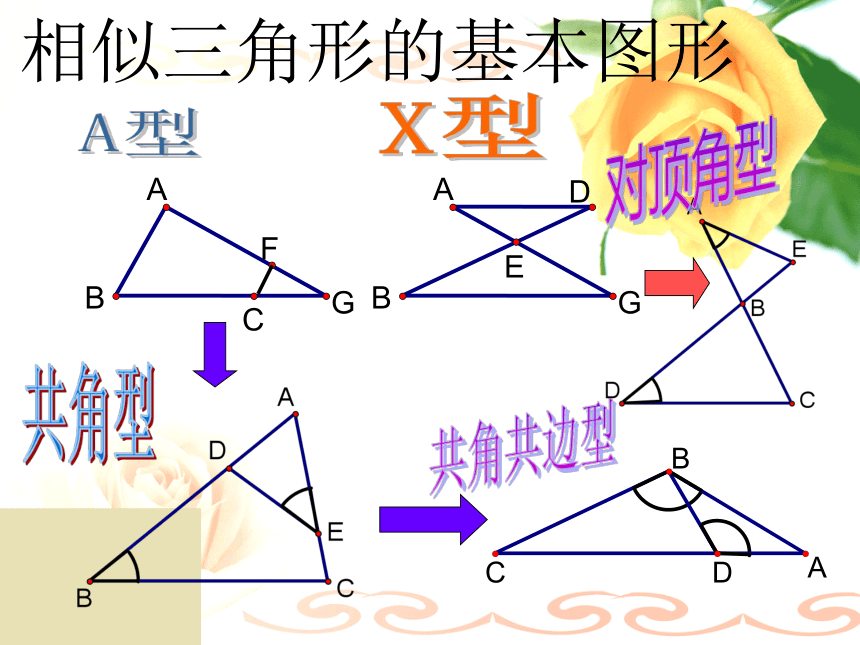
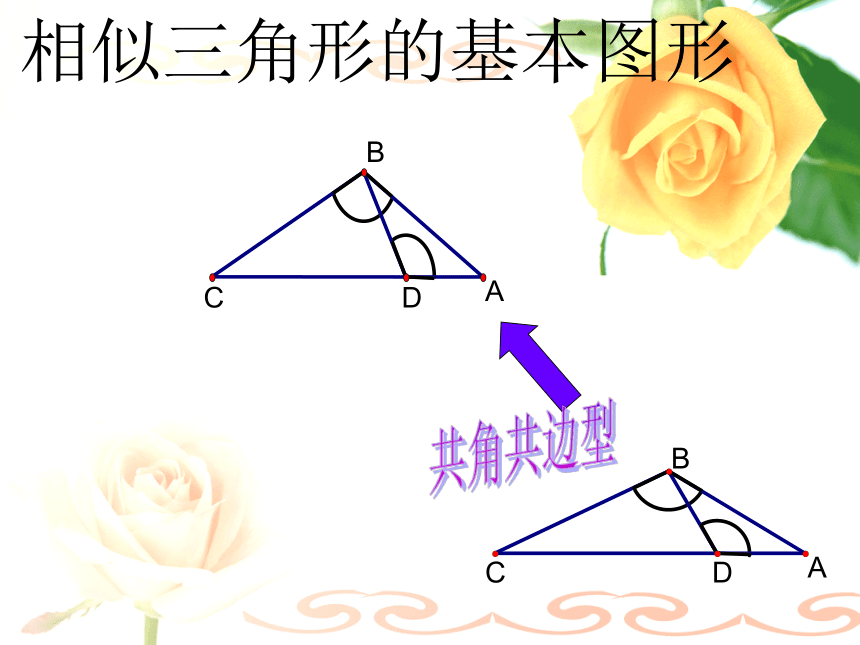
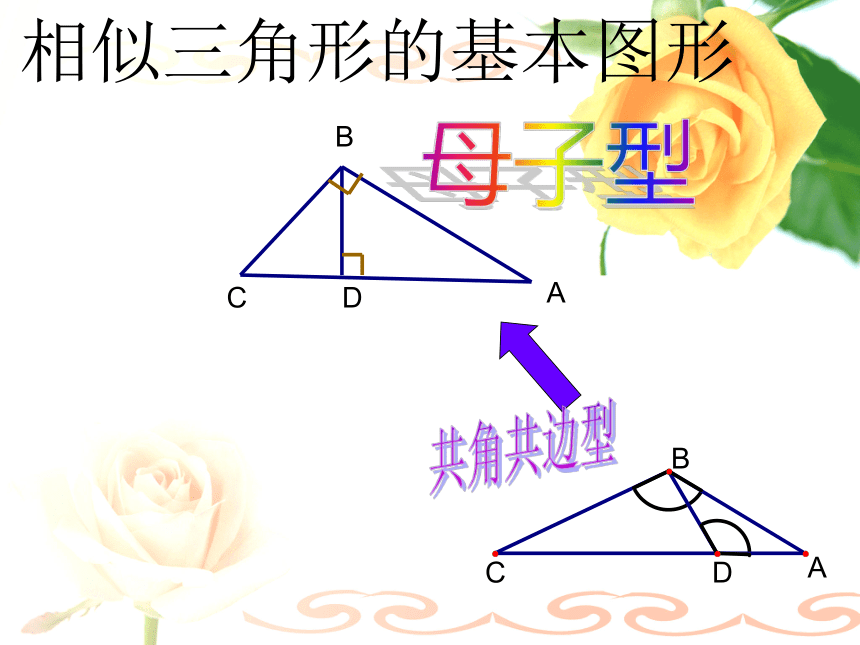
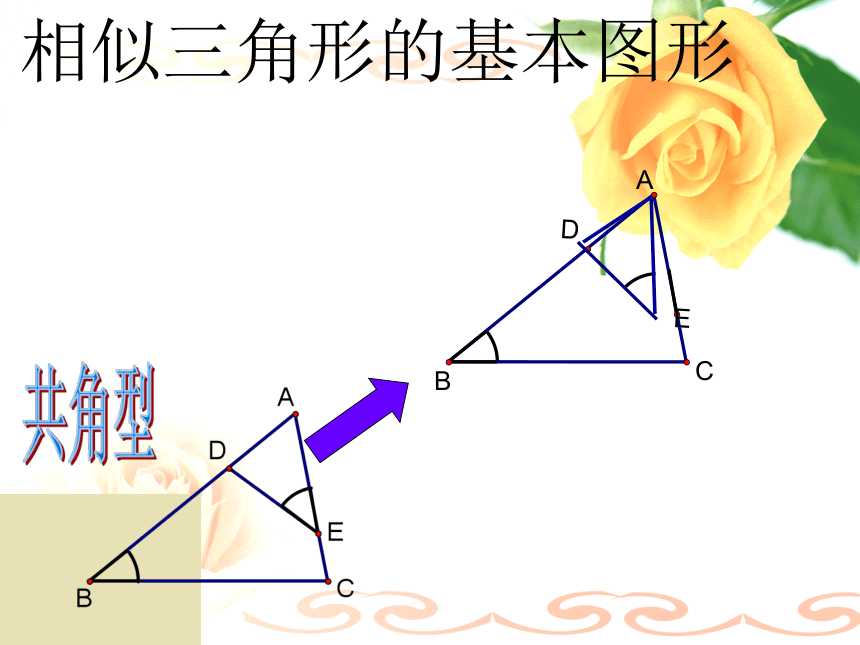
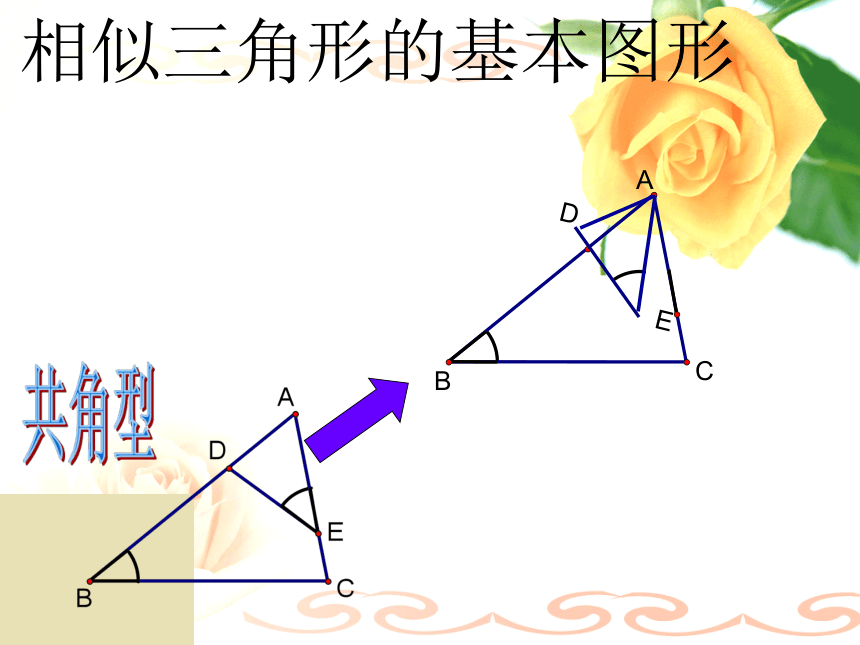
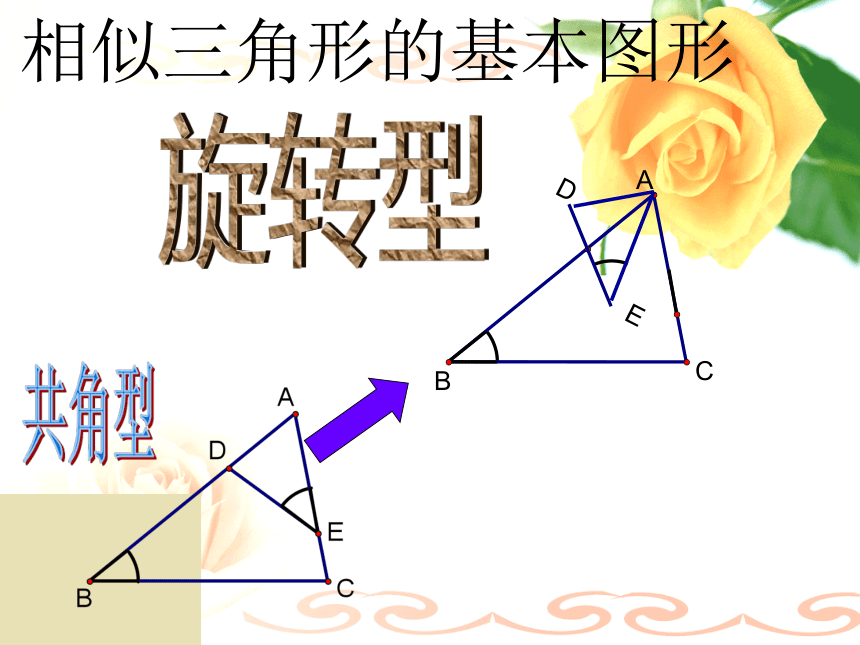
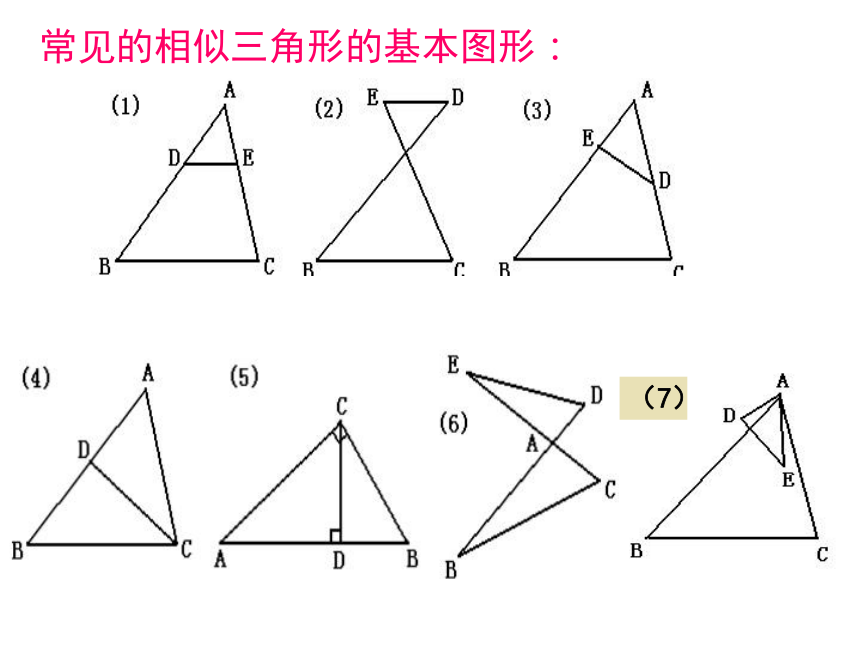
D课前热身相似三角形的基本图形A型FABGCX型共角型共角共边型相似三角形的基本图形A型FABGCX型共角型共角共边型EABGD对顶角型相似三角形的基本图形共角共边型相似三角形的基本图形共角共边型BCAD母子型相似三角形的基本图形共角型相似三角形的基本图形共角型相似三角形的基本图形共角型ABC旋转型常见的相似三角形的基本图形:应用举例一.填空选择题:
1.(1) △ ABC中,D,E分别是AB,AC上的点,且∠AED=∠ B那么△ AED ∽ △ ABC ,从而
ACCAEBD 解:∵∠AED=∠B, ∠A=∠A
∴△AED∽ △ABC (两角对应相等,两三角形相似)
∴
CAEBD(2) △ ABC中,AB的中 点为E,AC的中点为D, 连结ED,则△ AED与 △ ABC的相似比为 ______.1:2CAEBD 解 :∵D,E分别为AB,AC的中点
∴DE∥BC,且
∴ △ADE∽△ABC
即△ADE与△ABC的相似比为1:2
CAEBD2.如图,DE∥BC,
AD:DB=2:3,
则△ AED和△ ABC
的相似比为___.2:5CAEBD 解: ∵DE∥BC
∴△ADE∽△ABC
∵AD:DB=2:3
∴DB:AD=3:2
∴(DB+AD):AD=(2+3):3
即 AB:AD=5:2
∴AD:AB=2:5
即△ADE与△ABC
的相似比为2:5
CAEBD3. 已知三角形甲各边的比为3:4:6, 和它相似的三角形乙的最大边为10cm, 则三角形乙的最短边为______cm.5解3:设三角形甲为△ABC ,三角
形乙为 △DEF,且△DEF的最大
边为DE,最短边为EF
∵ △DEF∽△ABC
∴ DE:EF=6:3
即 10:EF=6:3
∴ EF=5cmACBFED4.等腰三角形ABC的腰长为18cm,底边长为6cm,在腰AC上取点D, 使△ABC∽ △BDC, 则DC=______.2cm解4.∵ △ABC ∽△BDC
即
∴ DC=2cmACBD5. 如图△ADE∽ △ACB
则DE:BC=_____ 。
1:3BCBDE3327解5.∵ △ADE∽△ACB
故
BCBDE33276. 如图D是△ABC边BC上一点,
连接AD,使△ABC∽△DBA 的条件是( ).
A. AC:BC=AD:BD
B. AC:BC=AB:AD
C. AB2=CD·BC
D. AB2=BD·BCDABCD7. D,E分别为△ABC的AB, AC上的点,且DE∥BC,
∠DCB=∠A,
把每两个相似的三角形称为一组,那么图中共有
相似三角形_____组。4ACBDE解7: ∵ DE∥BC
∴∠ADE= ∠B,
∠EDC=∠DCB=∠A
① ∵ DE∥BC
∴△ADE ∽ △ABC
② ∵ ∠A= ∠DCB, ∠ADE= ∠B
∴△ADE∽ △CBDACBDE解7: ③ ∵ △ADE ∽ △ABC
△ADE ∽ △CBD
∴ △ABC ∽ △CBD
④ ∵ ∠DCA= ∠DCE,
∠A= ∠EDC
∴ △ADC ∽ △DECACBDE二、证明题:
题1. D为△ABC中 AB边上一点, ∠ACD=∠ABC.
求证:AC2=AD·AB.
ABCDABCD分析:要证明AC2=AD·AB需要先将乘积式改写为
比例式
再证明AC,AD,AB所在的 两个三角形相似. 由已知 两 个三角形有二个角对应相等,所以两三角形相似, 本题可证。证明:∵∠ACD= ∠ ABC
∠A = ∠ A
∴ △ABC △ACD
∴
∴ AC2=AD·ABABCD题2. △ABC中,∠ BAC是直角,过斜边中点M而垂直于斜边BC的直线交CA的延长线于E,交AB于D,连结AM.
求证:
① △ MAD ~△ MEA
② AM2=MD · ME
CAEDBM分析:已知中与线段有关的条件仅有AM=BC/2=BM=MC,所以首先考虑用两个角对应相等去判定两个三角形相似。AM是△ MAD 与△ MEA 的公共边, 故是对应边MD,ME 的比例中项。 CAEDBM证明:①∵∠BAC=90°
M为斜边BC中点∴AM=BM=BC/2
∴ ∠B= ∠MAD
又∠B+∠BDM= ∠E+∠ADE= 90°
∠BDM= ∠ADE ∴∠B=∠E
∴∠MAD= ∠E
∵ ∠DMA= ∠AME
∴△MAD∽ △MEACAEDBM② ∵ △MAD∽ △MEA
∴
即AM2=MD·ME
CAEDBM题3. 如图,AB∥CD,AO=OB,DF=FB,DF交AC于E,
求证:ED2=EO · EC.分析:欲证 ED2=EO·EC即证:
只需证DE、EO、EC 所在的三角形相似。
AFBOCDE题3. 如图,AB∥CD,AO=OB,DF=FB,DF交AC于E,
求证:ED2=EO · EC.分析:欲证 ED2=EO·EC即证:
只需证DE、EO、EC 所在的三角形相似。
证明:∵ AB∥CD ∴∠C=∠A
∵ AO=OB,DF=FB
∴∠A=∠B,∠B=∠FDB
∴ ∠C= ∠FDB
又 ∠DEO= ∠DEC
∴ △EDC∽△EOD
AFBOCDE题4. 过平行四边形ABCD的一个顶点A作一直线分别交对角线BD,边BC, 边DC的延长线于E、F、G . 求证:
EA2 = EF· EG .CBADGFECBADGFE分析:要证明 EA2 = EF· EG ,
即 证明
成立,
而EA,EG,EF三条线段在同一直线上,无法构成两个三角形,此时应采用换线段,换比例的方法。
可证明: △AED∽△FEB, △AEB ∽ △GED.证明:∵ AD∥BF AB∥DC
∴△AED ∽△FEB
△AEB ∽△GED
CBADGFE题5. △ABC为锐角三角形, BD,CE为△的高 . 求证: △ ADE∽△ABC (用两种方法证明).AOBEDC 证明一:∵BD⊥AC,CE⊥AB
∴∠ABD+∠A=90° ∠ACE+∠A= 90° ∴ ∠ABD= ∠ACE
又 ∠A= ∠A ∴△ ABD ∽ △ ACE AOBEDC证明二: ∵∠BEO= ∠CDO , ∠ BOE=∠COD ∴ △BOE ∽ △COD 又∠BOC= ∠EOD
∴ △BOC ∽△EOD
∴ ∠1= ∠2
∵ ∠1+∠BCD=90°
∠2+∠3= 90°
∴ ∠ BCD= ∠3
又∵ ∠A= ∠A
∴ △ ADE∽ △ ABC AOBEDC 5. 如图△ABC中,AB=9,AC=6, D是边AB上一点 且AD=2,E是AC 上的点 ,则AE= 时, △ADE与△ABC相似?△ADE∽△ABC?8.如图,已知点P是边长为4的正方形ABCD内一点,且PB=3 BF⊥BP垂足是B请在射线BF上找一点M,使以点B、M、C为顶点的三角形与△ABP相似
. 则BM=
什么方法?什么基本图形?在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
(1) 求直线AB的解析式;
(2) 当t为何值时,△APQ与△AOB相似?
相似知识盘点对应角相等,对应边成比例。2.预备定理:3.判定定理1:4.判定定理2:5.判定定理3:1.定义:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。两角对应相等,两三角形相似。两边对应成比例且夹角相等, 两三角形相似。三边对应成比例,两三角形相似。6.直角三角形相似的判定定理: 斜边和一条直角边对应成比例,两直角三角形相似 如图,在□ABCD中,G是BC延长线上一点,AG与BD交于点E,与DC交于点F,则图中相似三角形共有( )
A. 3对
B. 4对
C. 5对
D. 6对
D课前热身相似三角形的基本图形A型FABGCX型共角型共角共边型相似三角形的基本图形A型FABGCX型共角型共角共边型EABGD对顶角型相似三角形的基本图形共角共边型相似三角形的基本图形共角共边型BCAD母子型相似三角形的基本图形共角型相似三角形的基本图形共角型相似三角形的基本图形共角型ABC旋转型常见的相似三角形的基本图形:应用举例一.填空选择题:
1.(1) △ ABC中,D,E分别是AB,AC上的点,且∠AED=∠ B那么△ AED ∽ △ ABC ,从而
ACCAEBD 解:∵∠AED=∠B, ∠A=∠A
∴△AED∽ △ABC (两角对应相等,两三角形相似)
∴
CAEBD(2) △ ABC中,AB的中 点为E,AC的中点为D, 连结ED,则△ AED与 △ ABC的相似比为 ______.1:2CAEBD 解 :∵D,E分别为AB,AC的中点
∴DE∥BC,且
∴ △ADE∽△ABC
即△ADE与△ABC的相似比为1:2
CAEBD2.如图,DE∥BC,
AD:DB=2:3,
则△ AED和△ ABC
的相似比为___.2:5CAEBD 解: ∵DE∥BC
∴△ADE∽△ABC
∵AD:DB=2:3
∴DB:AD=3:2
∴(DB+AD):AD=(2+3):3
即 AB:AD=5:2
∴AD:AB=2:5
即△ADE与△ABC
的相似比为2:5
CAEBD3. 已知三角形甲各边的比为3:4:6, 和它相似的三角形乙的最大边为10cm, 则三角形乙的最短边为______cm.5解3:设三角形甲为△ABC ,三角
形乙为 △DEF,且△DEF的最大
边为DE,最短边为EF
∵ △DEF∽△ABC
∴ DE:EF=6:3
即 10:EF=6:3
∴ EF=5cmACBFED4.等腰三角形ABC的腰长为18cm,底边长为6cm,在腰AC上取点D, 使△ABC∽ △BDC, 则DC=______.2cm解4.∵ △ABC ∽△BDC
即
∴ DC=2cmACBD5. 如图△ADE∽ △ACB
则DE:BC=_____ 。
1:3BCBDE3327解5.∵ △ADE∽△ACB
故
BCBDE33276. 如图D是△ABC边BC上一点,
连接AD,使△ABC∽△DBA 的条件是( ).
A. AC:BC=AD:BD
B. AC:BC=AB:AD
C. AB2=CD·BC
D. AB2=BD·BCDABCD7. D,E分别为△ABC的AB, AC上的点,且DE∥BC,
∠DCB=∠A,
把每两个相似的三角形称为一组,那么图中共有
相似三角形_____组。4ACBDE解7: ∵ DE∥BC
∴∠ADE= ∠B,
∠EDC=∠DCB=∠A
① ∵ DE∥BC
∴△ADE ∽ △ABC
② ∵ ∠A= ∠DCB, ∠ADE= ∠B
∴△ADE∽ △CBDACBDE解7: ③ ∵ △ADE ∽ △ABC
△ADE ∽ △CBD
∴ △ABC ∽ △CBD
④ ∵ ∠DCA= ∠DCE,
∠A= ∠EDC
∴ △ADC ∽ △DECACBDE二、证明题:
题1. D为△ABC中 AB边上一点, ∠ACD=∠ABC.
求证:AC2=AD·AB.
ABCDABCD分析:要证明AC2=AD·AB需要先将乘积式改写为
比例式
再证明AC,AD,AB所在的 两个三角形相似. 由已知 两 个三角形有二个角对应相等,所以两三角形相似, 本题可证。证明:∵∠ACD= ∠ ABC
∠A = ∠ A
∴ △ABC △ACD
∴
∴ AC2=AD·ABABCD题2. △ABC中,∠ BAC是直角,过斜边中点M而垂直于斜边BC的直线交CA的延长线于E,交AB于D,连结AM.
求证:
① △ MAD ~△ MEA
② AM2=MD · ME
CAEDBM分析:已知中与线段有关的条件仅有AM=BC/2=BM=MC,所以首先考虑用两个角对应相等去判定两个三角形相似。AM是△ MAD 与△ MEA 的公共边, 故是对应边MD,ME 的比例中项。 CAEDBM证明:①∵∠BAC=90°
M为斜边BC中点∴AM=BM=BC/2
∴ ∠B= ∠MAD
又∠B+∠BDM= ∠E+∠ADE= 90°
∠BDM= ∠ADE ∴∠B=∠E
∴∠MAD= ∠E
∵ ∠DMA= ∠AME
∴△MAD∽ △MEACAEDBM② ∵ △MAD∽ △MEA
∴
即AM2=MD·ME
CAEDBM题3. 如图,AB∥CD,AO=OB,DF=FB,DF交AC于E,
求证:ED2=EO · EC.分析:欲证 ED2=EO·EC即证:
只需证DE、EO、EC 所在的三角形相似。
AFBOCDE题3. 如图,AB∥CD,AO=OB,DF=FB,DF交AC于E,
求证:ED2=EO · EC.分析:欲证 ED2=EO·EC即证:
只需证DE、EO、EC 所在的三角形相似。
证明:∵ AB∥CD ∴∠C=∠A
∵ AO=OB,DF=FB
∴∠A=∠B,∠B=∠FDB
∴ ∠C= ∠FDB
又 ∠DEO= ∠DEC
∴ △EDC∽△EOD
AFBOCDE题4. 过平行四边形ABCD的一个顶点A作一直线分别交对角线BD,边BC, 边DC的延长线于E、F、G . 求证:
EA2 = EF· EG .CBADGFECBADGFE分析:要证明 EA2 = EF· EG ,
即 证明
成立,
而EA,EG,EF三条线段在同一直线上,无法构成两个三角形,此时应采用换线段,换比例的方法。
可证明: △AED∽△FEB, △AEB ∽ △GED.证明:∵ AD∥BF AB∥DC
∴△AED ∽△FEB
△AEB ∽△GED
CBADGFE题5. △ABC为锐角三角形, BD,CE为△的高 . 求证: △ ADE∽△ABC (用两种方法证明).AOBEDC 证明一:∵BD⊥AC,CE⊥AB
∴∠ABD+∠A=90° ∠ACE+∠A= 90° ∴ ∠ABD= ∠ACE
又 ∠A= ∠A ∴△ ABD ∽ △ ACE AOBEDC证明二: ∵∠BEO= ∠CDO , ∠ BOE=∠COD ∴ △BOE ∽ △COD 又∠BOC= ∠EOD
∴ △BOC ∽△EOD
∴ ∠1= ∠2
∵ ∠1+∠BCD=90°
∠2+∠3= 90°
∴ ∠ BCD= ∠3
又∵ ∠A= ∠A
∴ △ ADE∽ △ ABC AOBEDC 5. 如图△ABC中,AB=9,AC=6, D是边AB上一点 且AD=2,E是AC 上的点 ,则AE= 时, △ADE与△ABC相似?△ADE∽△ABC?8.如图,已知点P是边长为4的正方形ABCD内一点,且PB=3 BF⊥BP垂足是B请在射线BF上找一点M,使以点B、M、C为顶点的三角形与△ABP相似
. 则BM=
什么方法?什么基本图形?在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
(1) 求直线AB的解析式;
(2) 当t为何值时,△APQ与△AOB相似?
