2019秋北师大版九年级数学上册4.4探索三角形相似的条件学案(共4课时,无答案)
文档属性
| 名称 | 2019秋北师大版九年级数学上册4.4探索三角形相似的条件学案(共4课时,无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 65.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-06 21:57:47 | ||
图片预览



文档简介
4.4
探索三角形相似的条件
第1课时
两角分别相等的两个三角形相似
【学习目标】
1.熟练掌握相似三角形的定义;
2.熟练掌握三角形相似的判定方法;
3.能灵活运用判定方法判断两个三角形是否相似。
【回顾与思考】
1.对应角相等,对应边也相等的两个三角形全等,你还记得三角形全等的其他判别条件吗?
2.相似三角形的定义是什么?你认为判别两个三角形相似至少需要哪些条件?
【合作学习】
合探1
同学们观察我们的直角三角尺,直观上看它们是什么关系?到底需要满足几个条件两个三角形能够相相似?
合探2
与同伴合作,两个人分别画△ABC和△A′B′C′,使得∠A=∠A′都等于∠α,
∠B和∠B′都等于∠β,此时,∠C与∠C′相等吗?对应边的比相等吗?这样的两个三角形相似吗?改变∠α,∠β的大小,再试一试.
思考:在实际画图过程中,同学们画了几个角相等?为什么?
由此得到相似三角形的判定方法1:
【例题学习】
如图,D、E分别是△ABC边AB、AC上的点,DE∥BC,AB=7,AD=5,DE=10,求BC的长。
【巩固训练】
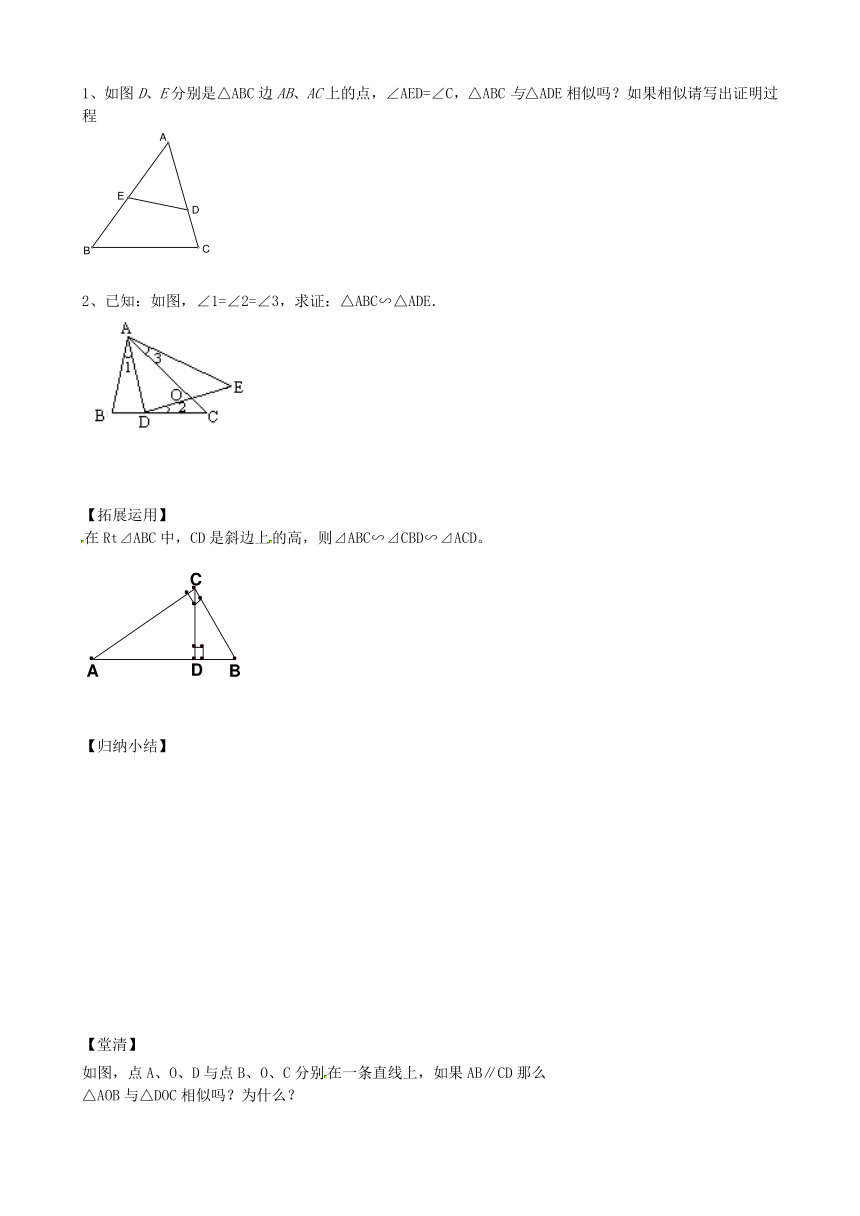
1、如图D、E分别是△ABC边AB、AC上的点,∠AED=∠C,△ABC与△ADE相似吗?如果相似请写出证明过程
2、已知:如图,∠1=∠2=∠3,求证:△ABC∽△ADE.
【拓展运用】
在Rt⊿ABC中,CD是斜边上的高,则⊿ABC∽⊿CBD∽⊿ACD。
【归纳小结】
【堂清】
如图,点A、O、D与点B、O、C分别在一条直线上,如果AB∥CD那么
△AOB与△DOC相似吗?为什么?
【作业】
1.已知:△ABC和△A′B′C′中,∠A=40°,∠B=70°,∠A′=40°,∠C′=70°.求证:△ABC∽△A′C′B′.
2、如图,△ABC中,DE‖BC,EF‖AB,证明:△ADE∽△EFC.
3、已知:如图,矩形ABCD中,E为BC上一点,DF⊥AE于F,若AB=4,AD=5,AE=6,求DF的长.
4、已知:如图,△ABC
的高AD、BE交于点F.求证:.
5、如图,AF∥CD,∠1=∠2,∠B=∠D,你能找出图中几对相似三角形?并逐一说明相似的理由.
【教学反思】
第2课时
两边成比例且夹角相等的两个三角形相似
【学习目标】
1.掌握三角形相似的判定方法2
2.会用相似三角形的判定方法2来判断、证明及计算.
【知识回顾】
1.如图,,添加一个条件使得∽
.
2.
两个三角形有两边成比例,它们一定相似吗?如果增加一角相等,你能说出有哪几种可能的情况吗?
【合作学习】
1.(1)画△ABC与△A′B′C′,使∠A=∠A′,和都等于给定的值k.设法比较
∠B与∠B′(或∠C与∠C′)的大小,△ABC与△A′B′C′相似吗?
(2)改变k值的大小,再试一试.
判定方法2:
2.如果△ABC与△A’B’C’两边成比例,且其中一边所对的角相等,那么这两个三角形一定相似吗?由此你能得到什么结论?
结论:
【例题学习】
例:
如图,D,E分别是△ABC的边AC,AB上的点,AE=1.5,AC=2,BC=3,且=,求DE的长.
【巩固练习】
如图,AB AE=AD AC,且∠1=∠2,求证:△ABC∽△ADE.
【拓展运用】
如图△ABC与△ADE有公共点A,∠DAB=∠CAE,试添加一个条件,使△ABC∽△ADE,并加以证明
【归纳小结】
【作业】
1.已知:如图,P为△ABC中线AD上的一点,且BD2=PD AD,
求证:△ADC∽△CDP.
2.在△ABC中,D为AC上的一点,CD:AD=1:2,∠BCA=45°,∠BDA=60°,AE⊥BD,E为垂足,连结CE(1)写出图中相等的线段(2)找出图中各对相似三角形,并加以证明
【教学反思】
第3课时
三边成比例的两个三角形相似
【学习目标】
1.掌握三角形相似的判定方法3
2.会用相似三角形的判定方法3来判断、证明及计算.
【知识回顾】
如图,,添加一个条件使得∽
.
有哪些不同的方法?
【合作学习】
画△ABC与△A′B′C′,使、和都等于给定的值k.
(1)设法比较∠A与∠A′的大小;
(2)△ABC与△A′B′C′相似吗?说说你的理由.
改变k值的大小,再试一试.
判定方法3:
【例题学习】
例:
如图,在△ABC和△ADE中,==
,∠BAD=20°,求∠CAE的度数.
【巩固练习】
依据下列条件,证明△ABC与△A′B′C′相似
AB=10
cm,BC=8cm,AC=16cm,A′B′=16cm,B′C′=12.8
cm,A′C′=25.6cm,
【归纳小结】
【教学反思】
第4课时
黄金分割
目标导航:⒈知道并理解黄金分割的定义,熟记黄金比:
⒉会找一条线段的黄金分割点。
⒊加深理解与掌握线段的比、成比例线段等有关知识。
学法指导:线段的黄金分割是成比例线段具体应用的一个典型例子,学习本节知识,首先要弄清线段黄金分割的意义,在此基础上通过动手操作,会将线段黄金分割。
新知探究:
㈠、黄金分割的定义:
1、动手操作,然后算一算,完成下面的填空:
度量线段AC、BC的长度,线段AC=
,BC=
,
计算=
、=
,
与的值
相等吗?
※在线段AB上,点C把线段AB分成两条线段
和
,如果
=
,
那么称线段AB被点C
,点C叫做线段AB的
,AC与AB的比叫做
。其中=
≈
※⑴、黄金分割是一种分割线段的方法,一条线段的黄金分割点有
个。
⑵、黄金比是两条线段的比,没有单位,它的比值为
,精确到0.001为
。
2、想一想:点C是线段AB的黄金分割点,则=
。
㈡、确定黄金分割点:
如图,已知线段AB,按照如下方法作图:
(1)经过点B作BD⊥AB,使BD=AB.
(2)连接AD,在DA上截取DE=DB.
(3)在AB上截取AC=AE.点C就是线段AB的黄金分割点。
㈢、黄金矩形:
宽与长的比是:的矩形叫做黄金矩形。
【绿色通道】
黄金分割是一种特殊的分割线段的方法,分割后,原线段、较长线段、较短线段之间有固定的比值关系,知道其中一条线段的长度,可以求出另外两条线段的长度;一条线段有两个黄金分割点。
课堂消化诊测:
⒈已知线段AB=2,点C是AB的黄金分割点,且AC>BC,则AC=
。
⒉已知如图,AB=2,点C是AB的黄金分割点,点D在AB上,且AD2=BD·AB,求的值。
⒊已知点P是线段AB的黄金分割点,AP>PB,设以AP为边的正方形的面积为S1,以PA、PB为邻边的矩形的面积为S2,S1与S2相等吗?说明理由。
⒋一个矩形是黄金矩形,若它的长为4cm,则它的宽为
。
超越自我:以长为2的线段AB为边作正方形ABCD,取AB的中点P,连结PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上,如图,(1)求AM、DM的长.
(2)说明AM2=AD·DM的理由。(3)根据(2)的结论你能找出图中的黄金分割点吗?
收获与困惑:(对照本节课的学习目标,谈谈你的收获与困惑,和同伴交流。)
50°
)
4
A
B
C
3.2
2
50°
)
E
D
F
1.6
A
B
A
B
C
D
C
1
探索三角形相似的条件
第1课时
两角分别相等的两个三角形相似
【学习目标】
1.熟练掌握相似三角形的定义;
2.熟练掌握三角形相似的判定方法;
3.能灵活运用判定方法判断两个三角形是否相似。
【回顾与思考】
1.对应角相等,对应边也相等的两个三角形全等,你还记得三角形全等的其他判别条件吗?
2.相似三角形的定义是什么?你认为判别两个三角形相似至少需要哪些条件?
【合作学习】
合探1
同学们观察我们的直角三角尺,直观上看它们是什么关系?到底需要满足几个条件两个三角形能够相相似?
合探2
与同伴合作,两个人分别画△ABC和△A′B′C′,使得∠A=∠A′都等于∠α,
∠B和∠B′都等于∠β,此时,∠C与∠C′相等吗?对应边的比相等吗?这样的两个三角形相似吗?改变∠α,∠β的大小,再试一试.
思考:在实际画图过程中,同学们画了几个角相等?为什么?
由此得到相似三角形的判定方法1:
【例题学习】
如图,D、E分别是△ABC边AB、AC上的点,DE∥BC,AB=7,AD=5,DE=10,求BC的长。
【巩固训练】
1、如图D、E分别是△ABC边AB、AC上的点,∠AED=∠C,△ABC与△ADE相似吗?如果相似请写出证明过程
2、已知:如图,∠1=∠2=∠3,求证:△ABC∽△ADE.
【拓展运用】
在Rt⊿ABC中,CD是斜边上的高,则⊿ABC∽⊿CBD∽⊿ACD。
【归纳小结】
【堂清】
如图,点A、O、D与点B、O、C分别在一条直线上,如果AB∥CD那么
△AOB与△DOC相似吗?为什么?
【作业】
1.已知:△ABC和△A′B′C′中,∠A=40°,∠B=70°,∠A′=40°,∠C′=70°.求证:△ABC∽△A′C′B′.
2、如图,△ABC中,DE‖BC,EF‖AB,证明:△ADE∽△EFC.
3、已知:如图,矩形ABCD中,E为BC上一点,DF⊥AE于F,若AB=4,AD=5,AE=6,求DF的长.
4、已知:如图,△ABC
的高AD、BE交于点F.求证:.
5、如图,AF∥CD,∠1=∠2,∠B=∠D,你能找出图中几对相似三角形?并逐一说明相似的理由.
【教学反思】
第2课时
两边成比例且夹角相等的两个三角形相似
【学习目标】
1.掌握三角形相似的判定方法2
2.会用相似三角形的判定方法2来判断、证明及计算.
【知识回顾】
1.如图,,添加一个条件使得∽
.
2.
两个三角形有两边成比例,它们一定相似吗?如果增加一角相等,你能说出有哪几种可能的情况吗?
【合作学习】
1.(1)画△ABC与△A′B′C′,使∠A=∠A′,和都等于给定的值k.设法比较
∠B与∠B′(或∠C与∠C′)的大小,△ABC与△A′B′C′相似吗?
(2)改变k值的大小,再试一试.
判定方法2:
2.如果△ABC与△A’B’C’两边成比例,且其中一边所对的角相等,那么这两个三角形一定相似吗?由此你能得到什么结论?
结论:
【例题学习】
例:
如图,D,E分别是△ABC的边AC,AB上的点,AE=1.5,AC=2,BC=3,且=,求DE的长.
【巩固练习】
如图,AB AE=AD AC,且∠1=∠2,求证:△ABC∽△ADE.
【拓展运用】
如图△ABC与△ADE有公共点A,∠DAB=∠CAE,试添加一个条件,使△ABC∽△ADE,并加以证明
【归纳小结】
【作业】
1.已知:如图,P为△ABC中线AD上的一点,且BD2=PD AD,
求证:△ADC∽△CDP.
2.在△ABC中,D为AC上的一点,CD:AD=1:2,∠BCA=45°,∠BDA=60°,AE⊥BD,E为垂足,连结CE(1)写出图中相等的线段(2)找出图中各对相似三角形,并加以证明
【教学反思】
第3课时
三边成比例的两个三角形相似
【学习目标】
1.掌握三角形相似的判定方法3
2.会用相似三角形的判定方法3来判断、证明及计算.
【知识回顾】
如图,,添加一个条件使得∽
.
有哪些不同的方法?
【合作学习】
画△ABC与△A′B′C′,使、和都等于给定的值k.
(1)设法比较∠A与∠A′的大小;
(2)△ABC与△A′B′C′相似吗?说说你的理由.
改变k值的大小,再试一试.
判定方法3:
【例题学习】
例:
如图,在△ABC和△ADE中,==
,∠BAD=20°,求∠CAE的度数.
【巩固练习】
依据下列条件,证明△ABC与△A′B′C′相似
AB=10
cm,BC=8cm,AC=16cm,A′B′=16cm,B′C′=12.8
cm,A′C′=25.6cm,
【归纳小结】
【教学反思】
第4课时
黄金分割
目标导航:⒈知道并理解黄金分割的定义,熟记黄金比:
⒉会找一条线段的黄金分割点。
⒊加深理解与掌握线段的比、成比例线段等有关知识。
学法指导:线段的黄金分割是成比例线段具体应用的一个典型例子,学习本节知识,首先要弄清线段黄金分割的意义,在此基础上通过动手操作,会将线段黄金分割。
新知探究:
㈠、黄金分割的定义:
1、动手操作,然后算一算,完成下面的填空:
度量线段AC、BC的长度,线段AC=
,BC=
,
计算=
、=
,
与的值
相等吗?
※在线段AB上,点C把线段AB分成两条线段
和
,如果
=
,
那么称线段AB被点C
,点C叫做线段AB的
,AC与AB的比叫做
。其中=
≈
※⑴、黄金分割是一种分割线段的方法,一条线段的黄金分割点有
个。
⑵、黄金比是两条线段的比,没有单位,它的比值为
,精确到0.001为
。
2、想一想:点C是线段AB的黄金分割点,则=
。
㈡、确定黄金分割点:
如图,已知线段AB,按照如下方法作图:
(1)经过点B作BD⊥AB,使BD=AB.
(2)连接AD,在DA上截取DE=DB.
(3)在AB上截取AC=AE.点C就是线段AB的黄金分割点。
㈢、黄金矩形:
宽与长的比是:的矩形叫做黄金矩形。
【绿色通道】
黄金分割是一种特殊的分割线段的方法,分割后,原线段、较长线段、较短线段之间有固定的比值关系,知道其中一条线段的长度,可以求出另外两条线段的长度;一条线段有两个黄金分割点。
课堂消化诊测:
⒈已知线段AB=2,点C是AB的黄金分割点,且AC>BC,则AC=
。
⒉已知如图,AB=2,点C是AB的黄金分割点,点D在AB上,且AD2=BD·AB,求的值。
⒊已知点P是线段AB的黄金分割点,AP>PB,设以AP为边的正方形的面积为S1,以PA、PB为邻边的矩形的面积为S2,S1与S2相等吗?说明理由。
⒋一个矩形是黄金矩形,若它的长为4cm,则它的宽为
。
超越自我:以长为2的线段AB为边作正方形ABCD,取AB的中点P,连结PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上,如图,(1)求AM、DM的长.
(2)说明AM2=AD·DM的理由。(3)根据(2)的结论你能找出图中的黄金分割点吗?
收获与困惑:(对照本节课的学习目标,谈谈你的收获与困惑,和同伴交流。)
50°
)
4
A
B
C
3.2
2
50°
)
E
D
F
1.6
A
B
A
B
C
D
C
1
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
