上海市沪教新版 八年级下册:20.3一次函数的应用 专项练习题 (解析版)
文档属性
| 名称 | 上海市沪教新版 八年级下册:20.3一次函数的应用 专项练习题 (解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-06 16:38:04 | ||
图片预览



文档简介
沪教新版 八年级下 第20章 一次函数的应用
一、选择题
1.某市出租车计费办法如图所示.根据图象信息,下列说法错误的是
A.出租车起步价是10元
B.在3千米内只收起步价
C.超过3千米部分每千米收3元
D.超过3千米时所需费用与之间的函数关系式是
2.某商场对顾客实行如下优惠方式:
(1)一次性购买金额不超过1万元,不予优惠;
(2)一次性购买金额超过1万元,超过部分9折优惠.
某人第一次在该商场付款8000元,第二次又在该商场付款19000元,如果他一次性购买的话可以节省
A.600元 B.800元 C.1000元 D.2700元
3.弹簧的长度与所挂物体的质量关系为一次函数,由图可知,不挂物体时,弹簧的长度为
A. B. C. D.
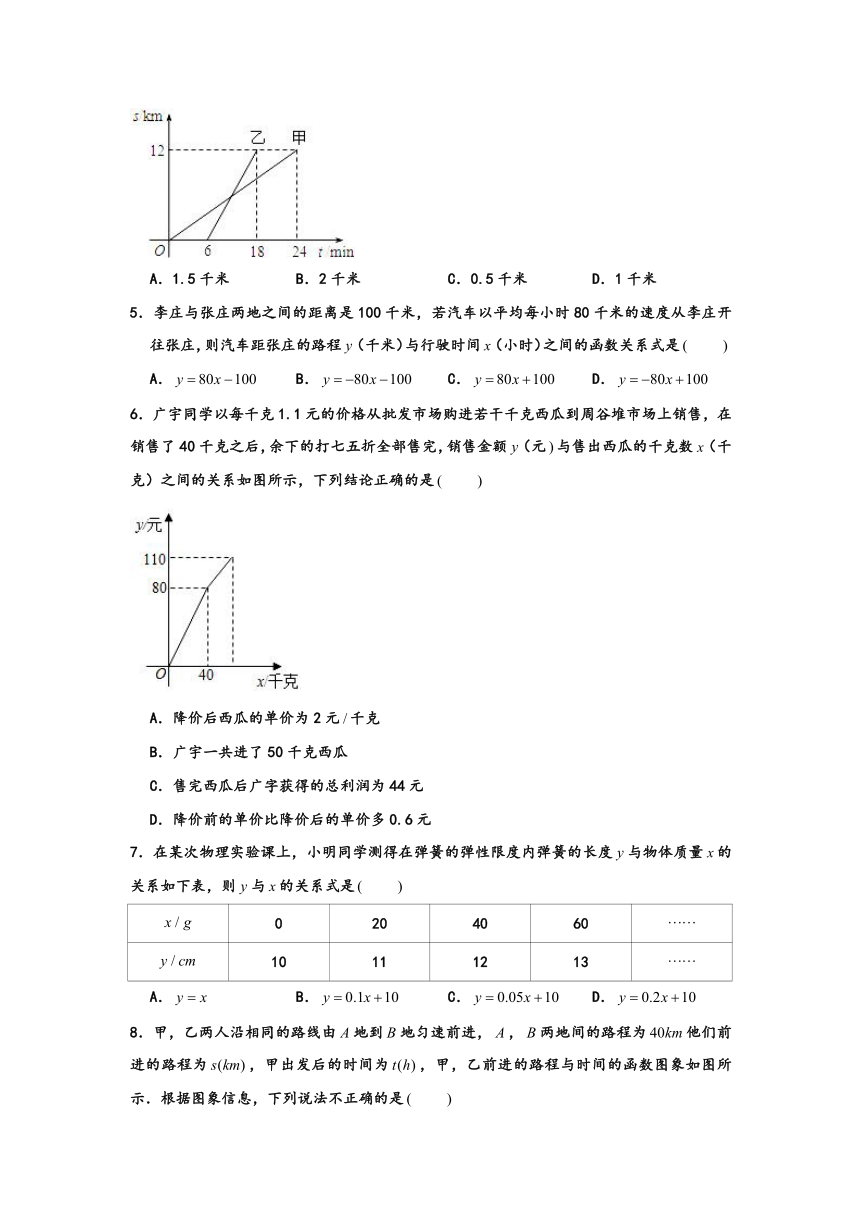
4.如图,表示甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.甲、乙两人前往目的地所行驶的路程随时间变化的函数图象,则每分钟乙比甲多行驶的路程为
A.1.5千米 B.2千米 C.0.5千米 D.1千米
5.李庄与张庄两地之间的距离是100千米,若汽车以平均每小时80千米的速度从李庄开往张庄,则汽车距张庄的路程(千米)与行驶时间(小时)之间的函数关系式是
A. B. C. D.
6.广宇同学以每千克1.1元的价格从批发市场购进若干千克西瓜到周谷堆市场上销售,在销售了40千克之后,余下的打七五折全部售完,销售金额(元与售出西瓜的千克数(千克)之间的关系如图所示,下列结论正确的是
A.降价后西瓜的单价为2元千克
B.广宇一共进了50千克西瓜
C.售完西瓜后广字获得的总利润为44元
D.降价前的单价比降价后的单价多0.6元
7.在某次物理实验课上,小明同学测得在弹簧的弹性限度内弹簧的长度与物体质量的关系如下表,则与的关系式是
0 20 40 60
10 11 12 13
A. B. C. D.
8.甲,乙两人沿相同的路线由地到地匀速前进,,两地间的路程为他们前进的路程为,甲出发后的时间为,甲,乙前进的路程与时间的函数图象如图所示.根据图象信息,下列说法不正确的是
A.甲的速度是 B.乙出发后与甲相遇
C.乙的速度是 D.甲比乙晚到地
9.某村办工厂今年前5个月生产某种产品的总量(件关于时间(月的函数图象如图所示,则该厂对这种产品来说
A.1月至3月每月生产总量逐月增加,4,5两月每月生产总量逐月减少
B.1月至3月每月生产总量逐月增加,4,5两月每月生产总量与3月份持平
C.1月至3月每月生产总量逐月增加,4,5两月均停止生产
D.1月至3月每月生产总量不变,4,5两月均停止生产
10.小明从家出发,沿一条直道跑步,经过一段时间原路返回,刚好在第回到家中,设小明出发第时的速度为,离家的距离为,与之间的函数关系如图所示,下列说法错误的是
A.小明出发第2分钟时离家
B.跑步过程中,小明离家的最远距离为
C.当时,与之间的函数表达式为
D.小明出发第5分钟时,开始按原路返回
二.填空题(共8小题)
11.已知等腰三角形的周长为20,腰长为,底边长为,则与的函数关系式为 ,自变量的取值范围是 .
12.生产某种产品所需的成本(万元)与数量(吨之间的关系如图所示,那么生产10吨这一产品所需成本为 万元.
13.已知某汽车油箱中的剩余油量(升是该汽车行驶时间(小时)的一次函数,其关系如下表:
(小时) 0 1 2 3
(升 100 92 84 76
由此可知,汽车行驶了 小时,油箱中的剩余油量为8升.
14.小明从地出发匀速走到地,小明经过(小时)后距离地(千米)的函数图象如图所示.则、两地距离为 千米.
15.如图,,分别表示甲乙两名学生运动的路程与时间的关系图象,图中与分别表示运动路程和时间,根据图象判断快者的速度比慢者的速度每秒快 米.
16.若弹簧的总长度是所挂重物的一次函数,图象如右图所示,那么不挂重物时,弹簧的长度是 .
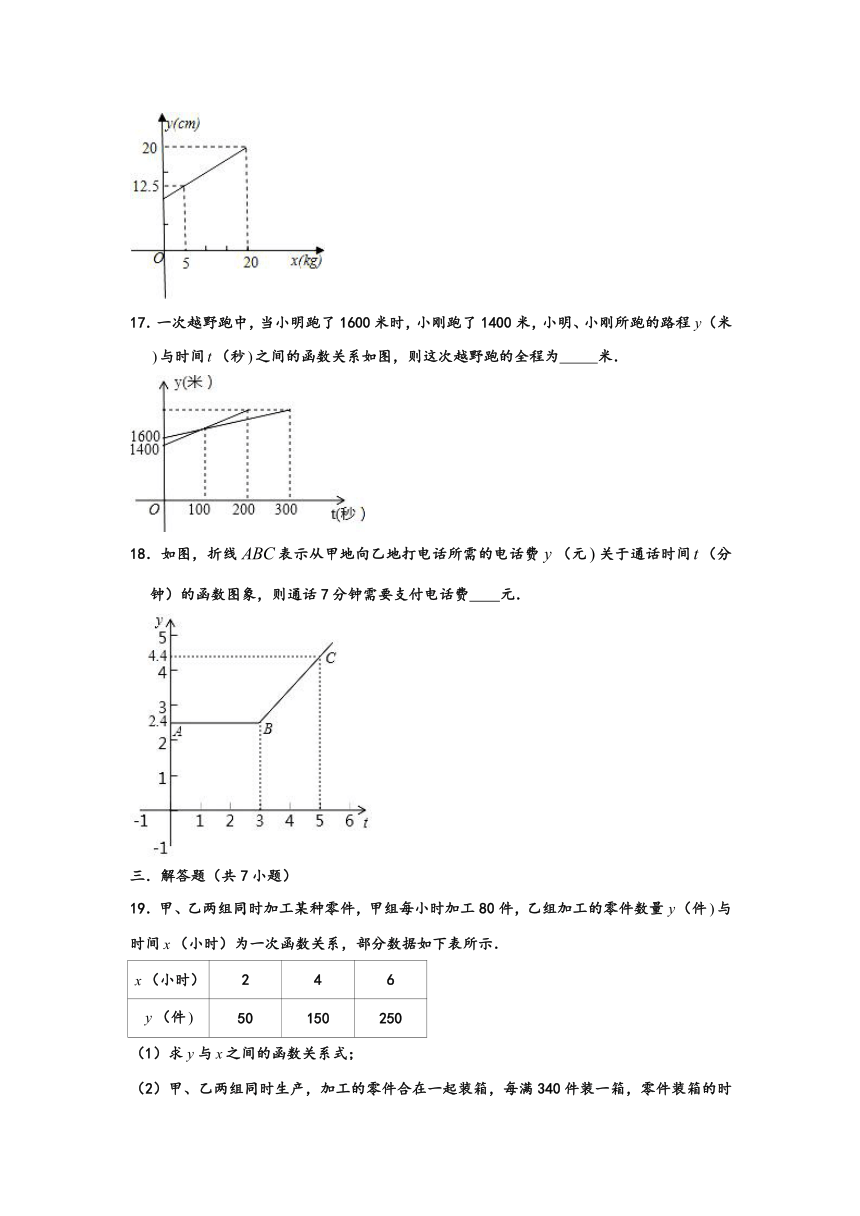
17.一次越野跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚所跑的路程(米与时间(秒之间的函数关系如图,则这次越野跑的全程为 米.
18.如图,折线表示从甲地向乙地打电话所需的电话费(元关于通话时间(分钟)的函数图象,则通话7分钟需要支付电话费 元.
三.解答题(共7小题)
19.甲、乙两组同时加工某种零件,甲组每小时加工80件,乙组加工的零件数量(件与时间(小时)为一次函数关系,部分数据如下表所示.
(小时) 2 4 6
(件 50 150 250
(1)求与之间的函数关系式;
(2)甲、乙两组同时生产,加工的零件合在一起装箱,每满340件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱?
20.为了响应“低碳环保,绿色出行”的公益活动,小燕和妈妈决定周日骑自行车去图书馆借书.她们同时从家出发,小燕先以150米分的速度骑行一段时间,休息了5分钟,再以米分钟的速度到达图书馆,而妈妈始终以120米分钟的速度骑行,两人行驶的路程(米与时间(分钟)的关系如图,请结合图象,解答下列问题:
(1)图书馆到小燕家的距离是 米;
(2) , , ;
(3)妈妈行驶的路程(米关于时间(分钟)的函数解析式是 ;定义域是 .
21.一果农带了若干千克自产的苹果进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又半价售完剩下的苹果.售出苹果千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)果农自带的零钱是多少?
(2)降价前他每千克苹果出售的价格是多少?
(3)降价售完剩余苹果后,这时他手中的钱(含备用零钱)是1120元,问果农一共带了多少千克苹果?
22.某乒乓球馆普通票价20元张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元张,每次凭卡不再收费;
②银卡售价150元张,每次凭卡另收10元;暑期普通票正常出售,两种优惠卡仅限暑期使用,不限次数.设打乒乓次时,所需总费用为元.
(1)分别写出选择银卡、普通票消费时,与之间的函数关系式;
(2)在同一个坐标系中,若三种消费方式对应的函数图象如图所示,请根据函数图象,写出选择哪种消费方式更合算.
23.某演唱会购买门票的方式有两种.
方式一:若单位赞助广告费10万元,则该单位所购门票的价格为每张0.02万元;
方式二:如图所示.
设购买门票张,总费用为万元,方式一中:总费用广告赞助费门票费.
(1)求方式一中与的函数关系式.
(2)若甲、乙两个单位分别采用方式一、方式二购买本场演唱会门票共400张,且乙单位购买超过100张,两单位共花费27.2万元,求甲、乙两单位各购买门票多少张?
24.某市为鼓励市民节约用水,自来水公司按分段收费标准收费,如图反映的是每月水费(元与用水量(吨之间的函数关系.
(1)当用水量超过10吨时,求关于的函数解析式(不必写定义域);
(2)按上述分段收费标准小聪家三、四月份分别交水费38元和27元,问四月份比三月份节约用水多少吨?
25.声音在空气中传播的速度是气温的函数,下表列出了一组不同温度时的声速.
气温 0 5 10 15 20
速度(米秒) 331 334 337 340 343
(1)求与之间的函数关系式;
(2)气温时,某人看到烟花燃放后才听到声响,那么此人与燃放烟花的所在地约相距多远?
参考答案
一.选择题(共10小题)
1.某市出租车计费办法如图所示.根据图象信息,下列说法错误的是
A.出租车起步价是10元
B.在3千米内只收起步价
C.超过3千米部分每千米收3元
D.超过3千米时所需费用与之间的函数关系式是
解:由图象可知,出租车的起步价是10元,在3千米内只收起步价,
设超过3千米的函数解析式为,则,解得,
超过3千米时所需费用与之间的函数关系式是,
超过3千米部分每千米收2元,
故、、正确,错误,
故选:.
2.某商场对顾客实行如下优惠方式:
(1)一次性购买金额不超过1万元,不予优惠;
(2)一次性购买金额超过1万元,超过部分9折优惠.
某人第一次在该商场付款8000元,第二次又在该商场付款19000元,如果他一次性购买的话可以节省
A.600元 B.800元 C.1000元 D.2700元
解:第一次购买付款8000元,可知没有得到打折优惠,
第二次付款19000元,获得了打折优惠,
设如果不打折第二次应付元,则,
解得:,
故他一次性购买的话需要付款:元,
则可节省元.
故选:.
3.弹簧的长度与所挂物体的质量关系为一次函数,由图可知,不挂物体时,弹簧的长度为
A. B. C. D.
解:设直线解析式为,由图象可知,直线过,两点,
代入得,解之得:,即,当时,,
即不挂物体时,弹簧的长度为.
故选:.
4.如图,表示甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.甲、乙两人前往目的地所行驶的路程随时间变化的函数图象,则每分钟乙比甲多行驶的路程为
A.1.5千米 B.2千米 C.0.5千米 D.1千米
解:由图可知甲的行驶速度为:,
乙的行驶速度为:,
故每分钟乙比甲多行驶的路程为,
故选:.
5.李庄与张庄两地之间的距离是100千米,若汽车以平均每小时80千米的速度从李庄开往张庄,则汽车距张庄的路程(千米)与行驶时间(小时)之间的函数关系式是
A. B. C. D.
解:
汽车的速度是平均每小时80千米,
它行驶小时走过的路程是,
汽车距张庄的路程(千米)与行驶时间(小时)之间的函数关系式是,
故选:.
6.广宇同学以每千克1.1元的价格从批发市场购进若干千克西瓜到周谷堆市场上销售,在销售了40千克之后,余下的打七五折全部售完,销售金额(元与售出西瓜的千克数(千克)之间的关系如图所示,下列结论正确的是
A.降价后西瓜的单价为2元千克
B.广宇一共进了50千克西瓜
C.售完西瓜后广字获得的总利润为44元
D.降价前的单价比降价后的单价多0.6元
解:由图可得,
西瓜降价前的价格为:元千克),西瓜降价后的价格为:(元千克),故选项错误,
(元,
降价前的单价比降价后的单价多0.5元,故选项错误;
广宇一共进了:千克西瓜,故选项错误;
售完西瓜后广字获得的总利润为:(元,故选项正确;
故选:.
7.在某次物理实验课上,小明同学测得在弹簧的弹性限度内弹簧的长度与物体质量的关系如下表,则与的关系式是
0 20 40 60
10 11 12 13
A. B. C. D.
解:在弹簧的弹性限度内弹簧的长度与物体质量的关系为一次函数关系,
设与的关系式为,
把,代入,可得
,
解得,
与的关系式为,
故选:.
8.甲,乙两人沿相同的路线由地到地匀速前进,,两地间的路程为他们前进的路程为,甲出发后的时间为,甲,乙前进的路程与时间的函数图象如图所示.根据图象信息,下列说法不正确的是
A.甲的速度是 B.乙出发后与甲相遇
C.乙的速度是 D.甲比乙晚到地
解:已知,两地间的路程为,由图可知,从地到,甲用时4小时,乙用时小时
甲的速度为,故正确;
乙的速度为,故选项正确;
设乙出发小时后与甲相遇,则
,故选项错误;
由图可知,甲4小时到达地,乙2小时到达地,从而甲比乙晚到2小时,故正确.
故选:.
9.某村办工厂今年前5个月生产某种产品的总量(件关于时间(月的函数图象如图所示,则该厂对这种产品来说
A.1月至3月每月生产总量逐月增加,4,5两月每月生产总量逐月减少
B.1月至3月每月生产总量逐月增加,4,5两月每月生产总量与3月份持平
C.1月至3月每月生产总量逐月增加,4,5两月均停止生产
D.1月至3月每月生产总量不变,4,5两月均停止生产
解:表示的总产量.前三个月的总产量直线上升,则1月至3月每月生产总量不变,而4、5两个月的产量不变,即停止生产.
故选:.
10.小明从家出发,沿一条直道跑步,经过一段时间原路返回,刚好在第回到家中,设小明出发第时的速度为,离家的距离为,与之间的函数关系如图所示,下列说法错误的是
A.小明出发第2分钟时离家
B.跑步过程中,小明离家的最远距离为
C.当时,与之间的函数表达式为
D.小明出发第5分钟时,开始按原路返回
解:由图象可得,
小明出发第2分钟时离家:,故选项正确;
跑步过程中,小明离家的最远距离为:,故选项正确;
当时,与之间的函数表达式为,故选项正确;
小明出发5分钟时,离家的距离为:,故此时小明没有达到离家的最远距离,没有按原路返回,还要继续向前走,故选项错误;
故选:.
二.填空题(共8小题)
11.已知等腰三角形的周长为20,腰长为,底边长为,则与的函数关系式为 ,自变量的取值范围是 .
解:,
,即,
两边之和大于第三边
,
综上可得.
故答案为:,.
12.生产某种产品所需的成本(万元)与数量(吨之间的关系如图所示,那么生产10吨这一产品所需成本为 万元.
解:设成本(万元)与数量(吨之间的关式是:,根据题意得:,
解得:,
则函数的解析式是:.
当吨时,万元.
故答案是:.
13.已知某汽车油箱中的剩余油量(升是该汽车行驶时间(小时)的一次函数,其关系如下表:
(小时) 0 1 2 3
(升 100 92 84 76
由此可知,汽车行驶了 11.5 小时,油箱中的剩余油量为8升.
解:设一次函数
将点和点代入得,解得
所以一次函数
令,即,解得
故答案为11.5
14.小明从地出发匀速走到地,小明经过(小时)后距离地(千米)的函数图象如图所示.则、两地距离为 20 千米.
解:根据题意可知小明从地出发匀速走到地需要4小时,走3小时后距离地5千米,所以小明的速度为5千米时,
所以、两地距离为:(千米).
故答案为:20
15.如图,,分别表示甲乙两名学生运动的路程与时间的关系图象,图中与分别表示运动路程和时间,根据图象判断快者的速度比慢者的速度每秒快 1.5 米.
解:观察图象知:甲跑64米用时8秒,速度为,
乙行驶52米用时8秒,速度为,
速度差为,
故答案为1.5.
16.若弹簧的总长度是所挂重物的一次函数,图象如右图所示,那么不挂重物时,弹簧的长度是 10 .
解:设一次函数的解析式为,
把、代入,
得,
解得,
一次函数的解析式为,
当时,,
即不挂重物时,弹簧的长度是.
故答案为10.
17.一次越野跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚所跑的路程(米与时间(秒之间的函数关系如图,则这次越野跑的全程为 2200 米.
解:设小明的速度为米秒,小刚的速度为米秒,由题意,得
,
解得:,
这次越野跑的全程为:米.
故答案为:2200.
18.如图,折线表示从甲地向乙地打电话所需的电话费(元关于通话时间(分钟)的函数图象,则通话7分钟需要支付电话费 6.4 元.
解:当通话时间在3分钟以内费用为2.4元,超出之后每分钟元
则通话7分钟费用为:元
故答案为:6.4
三.解答题(共7小题)
19.甲、乙两组同时加工某种零件,甲组每小时加工80件,乙组加工的零件数量(件与时间(小时)为一次函数关系,部分数据如下表所示.
(小时) 2 4 6
(件 50 150 250
(1)求与之间的函数关系式;
(2)甲、乙两组同时生产,加工的零件合在一起装箱,每满340件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱?
解:(1)设与之间的函数关系式为
把,,代入,
得解得
与之间的函数关系式为;
(2)设经过小时恰好装满第1箱,
根据题意得,
,
答:经过3小时恰好装满第1箱.
20.为了响应“低碳环保,绿色出行”的公益活动,小燕和妈妈决定周日骑自行车去图书馆借书.她们同时从家出发,小燕先以150米分的速度骑行一段时间,休息了5分钟,再以米分钟的速度到达图书馆,而妈妈始终以120米分钟的速度骑行,两人行驶的路程(米与时间(分钟)的关系如图,请结合图象,解答下列问题:
(1)图书馆到小燕家的距离是 3000 米;
(2) , , ;
(3)妈妈行驶的路程(米关于时间(分钟)的函数解析式是 ;定义域是 .
解:(1)由图象可得,
图书馆到小燕家的距离是3000米,
故答案为:3000;
(2),
,
,
故答案为:10,15,200;
(3)妈妈行驶的路程(米关于时间(分钟)的函数解析式是,
当时,,
则,得,
即妈妈行驶的路程(米关于时间(分钟)的函数解析式是,定义域是,
故答案为:,.
21.一果农带了若干千克自产的苹果进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又半价售完剩下的苹果.售出苹果千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)果农自带的零钱是多少?
(2)降价前他每千克苹果出售的价格是多少?
(3)降价售完剩余苹果后,这时他手中的钱(含备用零钱)是1120元,问果农一共带了多少千克苹果?
解:(1)由图可知,果农自带的零钱是40元;
(2)由图象可得,
(元千克),
答:降价前他每千克苹果出售的价格是12元千克;
(3)后来又按半价出售,则降价后的售价是元千克,
(千克),
(千克),
答:果农一共带了100千克苹果.
22.某乒乓球馆普通票价20元张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元张,每次凭卡不再收费;
②银卡售价150元张,每次凭卡另收10元;暑期普通票正常出售,两种优惠卡仅限暑期使用,不限次数.设打乒乓次时,所需总费用为元.
(1)分别写出选择银卡、普通票消费时,与之间的函数关系式;
(2)在同一个坐标系中,若三种消费方式对应的函数图象如图所示,请根据函数图象,写出选择哪种消费方式更合算.
解:(1)由题意可得,
选择银卡消费时,与之间的函数关系式为:,
选择普通票消费时,与之间的函数关系式为:;
(2)当时,得,
当时,得,
答:当打球次数不足15次时,选择普通票最合算,当打球次数介于15次到45次之间时,选择银卡最合算,当打球次数超过45次时,选择金卡最合算,当打球次数恰为15次时,选择普通票或银卡同为最合算,当打球次数恰为45次时,选择金卡或银卡同为最合算.
23.某演唱会购买门票的方式有两种.
方式一:若单位赞助广告费10万元,则该单位所购门票的价格为每张0.02万元;
方式二:如图所示.
设购买门票张,总费用为万元,方式一中:总费用广告赞助费门票费.
(1)求方式一中与的函数关系式.
(2)若甲、乙两个单位分别采用方式一、方式二购买本场演唱会门票共400张,且乙单位购买超过100张,两单位共花费27.2万元,求甲、乙两单位各购买门票多少张?
解:(1)方案一:单位赞助广告费10万元,该单位所购门票的价格为每张0.02万元,则;
(2)方案二:当时,设解析式为.
将,代入,
得,
解得,
所以.
设乙单位购买了张门票,则甲单位购买了张门票,根据题意得
,
解得,,
,
答:甲、乙两单位购买门票分别为270张和130张.
24.某市为鼓励市民节约用水,自来水公司按分段收费标准收费,如图反映的是每月水费(元与用水量(吨之间的函数关系.
(1)当用水量超过10吨时,求关于的函数解析式(不必写定义域);
(2)按上述分段收费标准小聪家三、四月份分别交水费38元和27元,问四月份比三月份节约用水多少吨?
解:(1)设当用水量超过10吨时,关于的函数解析式是,
,得,
即当用水量超过10吨时,关于的函数解析式是;
(2)将代入,得
,
解得,,
即三月份用水12吨,
四月份用水为:(吨,
四月份比三月份节约用水:(吨,
即四月份比三月份节约用水3吨.
25.声音在空气中传播的速度是气温的函数,下表列出了一组不同温度时的声速.
气温 0 5 10 15 20
速度(米秒) 331 334 337 340 343
(1)求与之间的函数关系式;
(2)气温时,某人看到烟花燃放后才听到声响,那么此人与燃放烟花的所在地约相距多远?
解:(1)根据表中数据画图象可知与成一次函数关系,
故设,取两点,代入关系式得
,解得
函数关系式为.
(2)把代入.
得,且.
光速非常快,传播时间可以忽略,
故此人与燃放烟花的所在地相距约.
一、选择题
1.某市出租车计费办法如图所示.根据图象信息,下列说法错误的是
A.出租车起步价是10元
B.在3千米内只收起步价
C.超过3千米部分每千米收3元
D.超过3千米时所需费用与之间的函数关系式是
2.某商场对顾客实行如下优惠方式:
(1)一次性购买金额不超过1万元,不予优惠;
(2)一次性购买金额超过1万元,超过部分9折优惠.
某人第一次在该商场付款8000元,第二次又在该商场付款19000元,如果他一次性购买的话可以节省
A.600元 B.800元 C.1000元 D.2700元
3.弹簧的长度与所挂物体的质量关系为一次函数,由图可知,不挂物体时,弹簧的长度为
A. B. C. D.
4.如图,表示甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.甲、乙两人前往目的地所行驶的路程随时间变化的函数图象,则每分钟乙比甲多行驶的路程为
A.1.5千米 B.2千米 C.0.5千米 D.1千米
5.李庄与张庄两地之间的距离是100千米,若汽车以平均每小时80千米的速度从李庄开往张庄,则汽车距张庄的路程(千米)与行驶时间(小时)之间的函数关系式是
A. B. C. D.
6.广宇同学以每千克1.1元的价格从批发市场购进若干千克西瓜到周谷堆市场上销售,在销售了40千克之后,余下的打七五折全部售完,销售金额(元与售出西瓜的千克数(千克)之间的关系如图所示,下列结论正确的是
A.降价后西瓜的单价为2元千克
B.广宇一共进了50千克西瓜
C.售完西瓜后广字获得的总利润为44元
D.降价前的单价比降价后的单价多0.6元
7.在某次物理实验课上,小明同学测得在弹簧的弹性限度内弹簧的长度与物体质量的关系如下表,则与的关系式是
0 20 40 60
10 11 12 13
A. B. C. D.
8.甲,乙两人沿相同的路线由地到地匀速前进,,两地间的路程为他们前进的路程为,甲出发后的时间为,甲,乙前进的路程与时间的函数图象如图所示.根据图象信息,下列说法不正确的是
A.甲的速度是 B.乙出发后与甲相遇
C.乙的速度是 D.甲比乙晚到地
9.某村办工厂今年前5个月生产某种产品的总量(件关于时间(月的函数图象如图所示,则该厂对这种产品来说
A.1月至3月每月生产总量逐月增加,4,5两月每月生产总量逐月减少
B.1月至3月每月生产总量逐月增加,4,5两月每月生产总量与3月份持平
C.1月至3月每月生产总量逐月增加,4,5两月均停止生产
D.1月至3月每月生产总量不变,4,5两月均停止生产
10.小明从家出发,沿一条直道跑步,经过一段时间原路返回,刚好在第回到家中,设小明出发第时的速度为,离家的距离为,与之间的函数关系如图所示,下列说法错误的是
A.小明出发第2分钟时离家
B.跑步过程中,小明离家的最远距离为
C.当时,与之间的函数表达式为
D.小明出发第5分钟时,开始按原路返回
二.填空题(共8小题)
11.已知等腰三角形的周长为20,腰长为,底边长为,则与的函数关系式为 ,自变量的取值范围是 .
12.生产某种产品所需的成本(万元)与数量(吨之间的关系如图所示,那么生产10吨这一产品所需成本为 万元.
13.已知某汽车油箱中的剩余油量(升是该汽车行驶时间(小时)的一次函数,其关系如下表:
(小时) 0 1 2 3
(升 100 92 84 76
由此可知,汽车行驶了 小时,油箱中的剩余油量为8升.
14.小明从地出发匀速走到地,小明经过(小时)后距离地(千米)的函数图象如图所示.则、两地距离为 千米.
15.如图,,分别表示甲乙两名学生运动的路程与时间的关系图象,图中与分别表示运动路程和时间,根据图象判断快者的速度比慢者的速度每秒快 米.
16.若弹簧的总长度是所挂重物的一次函数,图象如右图所示,那么不挂重物时,弹簧的长度是 .
17.一次越野跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚所跑的路程(米与时间(秒之间的函数关系如图,则这次越野跑的全程为 米.
18.如图,折线表示从甲地向乙地打电话所需的电话费(元关于通话时间(分钟)的函数图象,则通话7分钟需要支付电话费 元.
三.解答题(共7小题)
19.甲、乙两组同时加工某种零件,甲组每小时加工80件,乙组加工的零件数量(件与时间(小时)为一次函数关系,部分数据如下表所示.
(小时) 2 4 6
(件 50 150 250
(1)求与之间的函数关系式;
(2)甲、乙两组同时生产,加工的零件合在一起装箱,每满340件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱?
20.为了响应“低碳环保,绿色出行”的公益活动,小燕和妈妈决定周日骑自行车去图书馆借书.她们同时从家出发,小燕先以150米分的速度骑行一段时间,休息了5分钟,再以米分钟的速度到达图书馆,而妈妈始终以120米分钟的速度骑行,两人行驶的路程(米与时间(分钟)的关系如图,请结合图象,解答下列问题:
(1)图书馆到小燕家的距离是 米;
(2) , , ;
(3)妈妈行驶的路程(米关于时间(分钟)的函数解析式是 ;定义域是 .
21.一果农带了若干千克自产的苹果进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又半价售完剩下的苹果.售出苹果千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)果农自带的零钱是多少?
(2)降价前他每千克苹果出售的价格是多少?
(3)降价售完剩余苹果后,这时他手中的钱(含备用零钱)是1120元,问果农一共带了多少千克苹果?
22.某乒乓球馆普通票价20元张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元张,每次凭卡不再收费;
②银卡售价150元张,每次凭卡另收10元;暑期普通票正常出售,两种优惠卡仅限暑期使用,不限次数.设打乒乓次时,所需总费用为元.
(1)分别写出选择银卡、普通票消费时,与之间的函数关系式;
(2)在同一个坐标系中,若三种消费方式对应的函数图象如图所示,请根据函数图象,写出选择哪种消费方式更合算.
23.某演唱会购买门票的方式有两种.
方式一:若单位赞助广告费10万元,则该单位所购门票的价格为每张0.02万元;
方式二:如图所示.
设购买门票张,总费用为万元,方式一中:总费用广告赞助费门票费.
(1)求方式一中与的函数关系式.
(2)若甲、乙两个单位分别采用方式一、方式二购买本场演唱会门票共400张,且乙单位购买超过100张,两单位共花费27.2万元,求甲、乙两单位各购买门票多少张?
24.某市为鼓励市民节约用水,自来水公司按分段收费标准收费,如图反映的是每月水费(元与用水量(吨之间的函数关系.
(1)当用水量超过10吨时,求关于的函数解析式(不必写定义域);
(2)按上述分段收费标准小聪家三、四月份分别交水费38元和27元,问四月份比三月份节约用水多少吨?
25.声音在空气中传播的速度是气温的函数,下表列出了一组不同温度时的声速.
气温 0 5 10 15 20
速度(米秒) 331 334 337 340 343
(1)求与之间的函数关系式;
(2)气温时,某人看到烟花燃放后才听到声响,那么此人与燃放烟花的所在地约相距多远?
参考答案
一.选择题(共10小题)
1.某市出租车计费办法如图所示.根据图象信息,下列说法错误的是
A.出租车起步价是10元
B.在3千米内只收起步价
C.超过3千米部分每千米收3元
D.超过3千米时所需费用与之间的函数关系式是
解:由图象可知,出租车的起步价是10元,在3千米内只收起步价,
设超过3千米的函数解析式为,则,解得,
超过3千米时所需费用与之间的函数关系式是,
超过3千米部分每千米收2元,
故、、正确,错误,
故选:.
2.某商场对顾客实行如下优惠方式:
(1)一次性购买金额不超过1万元,不予优惠;
(2)一次性购买金额超过1万元,超过部分9折优惠.
某人第一次在该商场付款8000元,第二次又在该商场付款19000元,如果他一次性购买的话可以节省
A.600元 B.800元 C.1000元 D.2700元
解:第一次购买付款8000元,可知没有得到打折优惠,
第二次付款19000元,获得了打折优惠,
设如果不打折第二次应付元,则,
解得:,
故他一次性购买的话需要付款:元,
则可节省元.
故选:.
3.弹簧的长度与所挂物体的质量关系为一次函数,由图可知,不挂物体时,弹簧的长度为
A. B. C. D.
解:设直线解析式为,由图象可知,直线过,两点,
代入得,解之得:,即,当时,,
即不挂物体时,弹簧的长度为.
故选:.
4.如图,表示甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.甲、乙两人前往目的地所行驶的路程随时间变化的函数图象,则每分钟乙比甲多行驶的路程为
A.1.5千米 B.2千米 C.0.5千米 D.1千米
解:由图可知甲的行驶速度为:,
乙的行驶速度为:,
故每分钟乙比甲多行驶的路程为,
故选:.
5.李庄与张庄两地之间的距离是100千米,若汽车以平均每小时80千米的速度从李庄开往张庄,则汽车距张庄的路程(千米)与行驶时间(小时)之间的函数关系式是
A. B. C. D.
解:
汽车的速度是平均每小时80千米,
它行驶小时走过的路程是,
汽车距张庄的路程(千米)与行驶时间(小时)之间的函数关系式是,
故选:.
6.广宇同学以每千克1.1元的价格从批发市场购进若干千克西瓜到周谷堆市场上销售,在销售了40千克之后,余下的打七五折全部售完,销售金额(元与售出西瓜的千克数(千克)之间的关系如图所示,下列结论正确的是
A.降价后西瓜的单价为2元千克
B.广宇一共进了50千克西瓜
C.售完西瓜后广字获得的总利润为44元
D.降价前的单价比降价后的单价多0.6元
解:由图可得,
西瓜降价前的价格为:元千克),西瓜降价后的价格为:(元千克),故选项错误,
(元,
降价前的单价比降价后的单价多0.5元,故选项错误;
广宇一共进了:千克西瓜,故选项错误;
售完西瓜后广字获得的总利润为:(元,故选项正确;
故选:.
7.在某次物理实验课上,小明同学测得在弹簧的弹性限度内弹簧的长度与物体质量的关系如下表,则与的关系式是
0 20 40 60
10 11 12 13
A. B. C. D.
解:在弹簧的弹性限度内弹簧的长度与物体质量的关系为一次函数关系,
设与的关系式为,
把,代入,可得
,
解得,
与的关系式为,
故选:.
8.甲,乙两人沿相同的路线由地到地匀速前进,,两地间的路程为他们前进的路程为,甲出发后的时间为,甲,乙前进的路程与时间的函数图象如图所示.根据图象信息,下列说法不正确的是
A.甲的速度是 B.乙出发后与甲相遇
C.乙的速度是 D.甲比乙晚到地
解:已知,两地间的路程为,由图可知,从地到,甲用时4小时,乙用时小时
甲的速度为,故正确;
乙的速度为,故选项正确;
设乙出发小时后与甲相遇,则
,故选项错误;
由图可知,甲4小时到达地,乙2小时到达地,从而甲比乙晚到2小时,故正确.
故选:.
9.某村办工厂今年前5个月生产某种产品的总量(件关于时间(月的函数图象如图所示,则该厂对这种产品来说
A.1月至3月每月生产总量逐月增加,4,5两月每月生产总量逐月减少
B.1月至3月每月生产总量逐月增加,4,5两月每月生产总量与3月份持平
C.1月至3月每月生产总量逐月增加,4,5两月均停止生产
D.1月至3月每月生产总量不变,4,5两月均停止生产
解:表示的总产量.前三个月的总产量直线上升,则1月至3月每月生产总量不变,而4、5两个月的产量不变,即停止生产.
故选:.
10.小明从家出发,沿一条直道跑步,经过一段时间原路返回,刚好在第回到家中,设小明出发第时的速度为,离家的距离为,与之间的函数关系如图所示,下列说法错误的是
A.小明出发第2分钟时离家
B.跑步过程中,小明离家的最远距离为
C.当时,与之间的函数表达式为
D.小明出发第5分钟时,开始按原路返回
解:由图象可得,
小明出发第2分钟时离家:,故选项正确;
跑步过程中,小明离家的最远距离为:,故选项正确;
当时,与之间的函数表达式为,故选项正确;
小明出发5分钟时,离家的距离为:,故此时小明没有达到离家的最远距离,没有按原路返回,还要继续向前走,故选项错误;
故选:.
二.填空题(共8小题)
11.已知等腰三角形的周长为20,腰长为,底边长为,则与的函数关系式为 ,自变量的取值范围是 .
解:,
,即,
两边之和大于第三边
,
综上可得.
故答案为:,.
12.生产某种产品所需的成本(万元)与数量(吨之间的关系如图所示,那么生产10吨这一产品所需成本为 万元.
解:设成本(万元)与数量(吨之间的关式是:,根据题意得:,
解得:,
则函数的解析式是:.
当吨时,万元.
故答案是:.
13.已知某汽车油箱中的剩余油量(升是该汽车行驶时间(小时)的一次函数,其关系如下表:
(小时) 0 1 2 3
(升 100 92 84 76
由此可知,汽车行驶了 11.5 小时,油箱中的剩余油量为8升.
解:设一次函数
将点和点代入得,解得
所以一次函数
令,即,解得
故答案为11.5
14.小明从地出发匀速走到地,小明经过(小时)后距离地(千米)的函数图象如图所示.则、两地距离为 20 千米.
解:根据题意可知小明从地出发匀速走到地需要4小时,走3小时后距离地5千米,所以小明的速度为5千米时,
所以、两地距离为:(千米).
故答案为:20
15.如图,,分别表示甲乙两名学生运动的路程与时间的关系图象,图中与分别表示运动路程和时间,根据图象判断快者的速度比慢者的速度每秒快 1.5 米.
解:观察图象知:甲跑64米用时8秒,速度为,
乙行驶52米用时8秒,速度为,
速度差为,
故答案为1.5.
16.若弹簧的总长度是所挂重物的一次函数,图象如右图所示,那么不挂重物时,弹簧的长度是 10 .
解:设一次函数的解析式为,
把、代入,
得,
解得,
一次函数的解析式为,
当时,,
即不挂重物时,弹簧的长度是.
故答案为10.
17.一次越野跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚所跑的路程(米与时间(秒之间的函数关系如图,则这次越野跑的全程为 2200 米.
解:设小明的速度为米秒,小刚的速度为米秒,由题意,得
,
解得:,
这次越野跑的全程为:米.
故答案为:2200.
18.如图,折线表示从甲地向乙地打电话所需的电话费(元关于通话时间(分钟)的函数图象,则通话7分钟需要支付电话费 6.4 元.
解:当通话时间在3分钟以内费用为2.4元,超出之后每分钟元
则通话7分钟费用为:元
故答案为:6.4
三.解答题(共7小题)
19.甲、乙两组同时加工某种零件,甲组每小时加工80件,乙组加工的零件数量(件与时间(小时)为一次函数关系,部分数据如下表所示.
(小时) 2 4 6
(件 50 150 250
(1)求与之间的函数关系式;
(2)甲、乙两组同时生产,加工的零件合在一起装箱,每满340件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱?
解:(1)设与之间的函数关系式为
把,,代入,
得解得
与之间的函数关系式为;
(2)设经过小时恰好装满第1箱,
根据题意得,
,
答:经过3小时恰好装满第1箱.
20.为了响应“低碳环保,绿色出行”的公益活动,小燕和妈妈决定周日骑自行车去图书馆借书.她们同时从家出发,小燕先以150米分的速度骑行一段时间,休息了5分钟,再以米分钟的速度到达图书馆,而妈妈始终以120米分钟的速度骑行,两人行驶的路程(米与时间(分钟)的关系如图,请结合图象,解答下列问题:
(1)图书馆到小燕家的距离是 3000 米;
(2) , , ;
(3)妈妈行驶的路程(米关于时间(分钟)的函数解析式是 ;定义域是 .
解:(1)由图象可得,
图书馆到小燕家的距离是3000米,
故答案为:3000;
(2),
,
,
故答案为:10,15,200;
(3)妈妈行驶的路程(米关于时间(分钟)的函数解析式是,
当时,,
则,得,
即妈妈行驶的路程(米关于时间(分钟)的函数解析式是,定义域是,
故答案为:,.
21.一果农带了若干千克自产的苹果进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又半价售完剩下的苹果.售出苹果千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)果农自带的零钱是多少?
(2)降价前他每千克苹果出售的价格是多少?
(3)降价售完剩余苹果后,这时他手中的钱(含备用零钱)是1120元,问果农一共带了多少千克苹果?
解:(1)由图可知,果农自带的零钱是40元;
(2)由图象可得,
(元千克),
答:降价前他每千克苹果出售的价格是12元千克;
(3)后来又按半价出售,则降价后的售价是元千克,
(千克),
(千克),
答:果农一共带了100千克苹果.
22.某乒乓球馆普通票价20元张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元张,每次凭卡不再收费;
②银卡售价150元张,每次凭卡另收10元;暑期普通票正常出售,两种优惠卡仅限暑期使用,不限次数.设打乒乓次时,所需总费用为元.
(1)分别写出选择银卡、普通票消费时,与之间的函数关系式;
(2)在同一个坐标系中,若三种消费方式对应的函数图象如图所示,请根据函数图象,写出选择哪种消费方式更合算.
解:(1)由题意可得,
选择银卡消费时,与之间的函数关系式为:,
选择普通票消费时,与之间的函数关系式为:;
(2)当时,得,
当时,得,
答:当打球次数不足15次时,选择普通票最合算,当打球次数介于15次到45次之间时,选择银卡最合算,当打球次数超过45次时,选择金卡最合算,当打球次数恰为15次时,选择普通票或银卡同为最合算,当打球次数恰为45次时,选择金卡或银卡同为最合算.
23.某演唱会购买门票的方式有两种.
方式一:若单位赞助广告费10万元,则该单位所购门票的价格为每张0.02万元;
方式二:如图所示.
设购买门票张,总费用为万元,方式一中:总费用广告赞助费门票费.
(1)求方式一中与的函数关系式.
(2)若甲、乙两个单位分别采用方式一、方式二购买本场演唱会门票共400张,且乙单位购买超过100张,两单位共花费27.2万元,求甲、乙两单位各购买门票多少张?
解:(1)方案一:单位赞助广告费10万元,该单位所购门票的价格为每张0.02万元,则;
(2)方案二:当时,设解析式为.
将,代入,
得,
解得,
所以.
设乙单位购买了张门票,则甲单位购买了张门票,根据题意得
,
解得,,
,
答:甲、乙两单位购买门票分别为270张和130张.
24.某市为鼓励市民节约用水,自来水公司按分段收费标准收费,如图反映的是每月水费(元与用水量(吨之间的函数关系.
(1)当用水量超过10吨时,求关于的函数解析式(不必写定义域);
(2)按上述分段收费标准小聪家三、四月份分别交水费38元和27元,问四月份比三月份节约用水多少吨?
解:(1)设当用水量超过10吨时,关于的函数解析式是,
,得,
即当用水量超过10吨时,关于的函数解析式是;
(2)将代入,得
,
解得,,
即三月份用水12吨,
四月份用水为:(吨,
四月份比三月份节约用水:(吨,
即四月份比三月份节约用水3吨.
25.声音在空气中传播的速度是气温的函数,下表列出了一组不同温度时的声速.
气温 0 5 10 15 20
速度(米秒) 331 334 337 340 343
(1)求与之间的函数关系式;
(2)气温时,某人看到烟花燃放后才听到声响,那么此人与燃放烟花的所在地约相距多远?
解:(1)根据表中数据画图象可知与成一次函数关系,
故设,取两点,代入关系式得
,解得
函数关系式为.
(2)把代入.
得,且.
光速非常快,传播时间可以忽略,
故此人与燃放烟花的所在地相距约.
