2020年春人教版九年级数学下册:27.2.1.3 由两角判定三角形相似培优试题 (含答案)
文档属性
| 名称 | 2020年春人教版九年级数学下册:27.2.1.3 由两角判定三角形相似培优试题 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 290.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-06 16:34:29 | ||
图片预览


文档简介
人教版九年级数学下册27.2.1.3《由两角判定三角形相似》培优训练
一.选择题(本大题共10小题,每小题3分,共30分)
1.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则下列说法中错误的是( )
A.△ACD∽△CBD B.△ACD∽△ABC
C.△BCD∽△ABC D.△BCD∽△BAC
2.已知一个三角形的两个内角分别是40°,60°,另一个三角形的两个内角分别是40°,80°,则这两个三角形( )
A.一定不相似 B.不一定相似
C.一定相似 D.不能确定
3. 如图,在△ABC中,点D,E分别在AB,AC上,添加下列条件不能判定△AED∽△ABC的是( )
A.∠AED=∠B B.∠ADE=∠C
C.∠ADE=∠B D.=
4.如图,在△ABC中,AE交BC于点D,∠C=∠E,AD∶DE=3∶5,AE=8,BD=4,则DC的长等于( )
A. B. C. D.
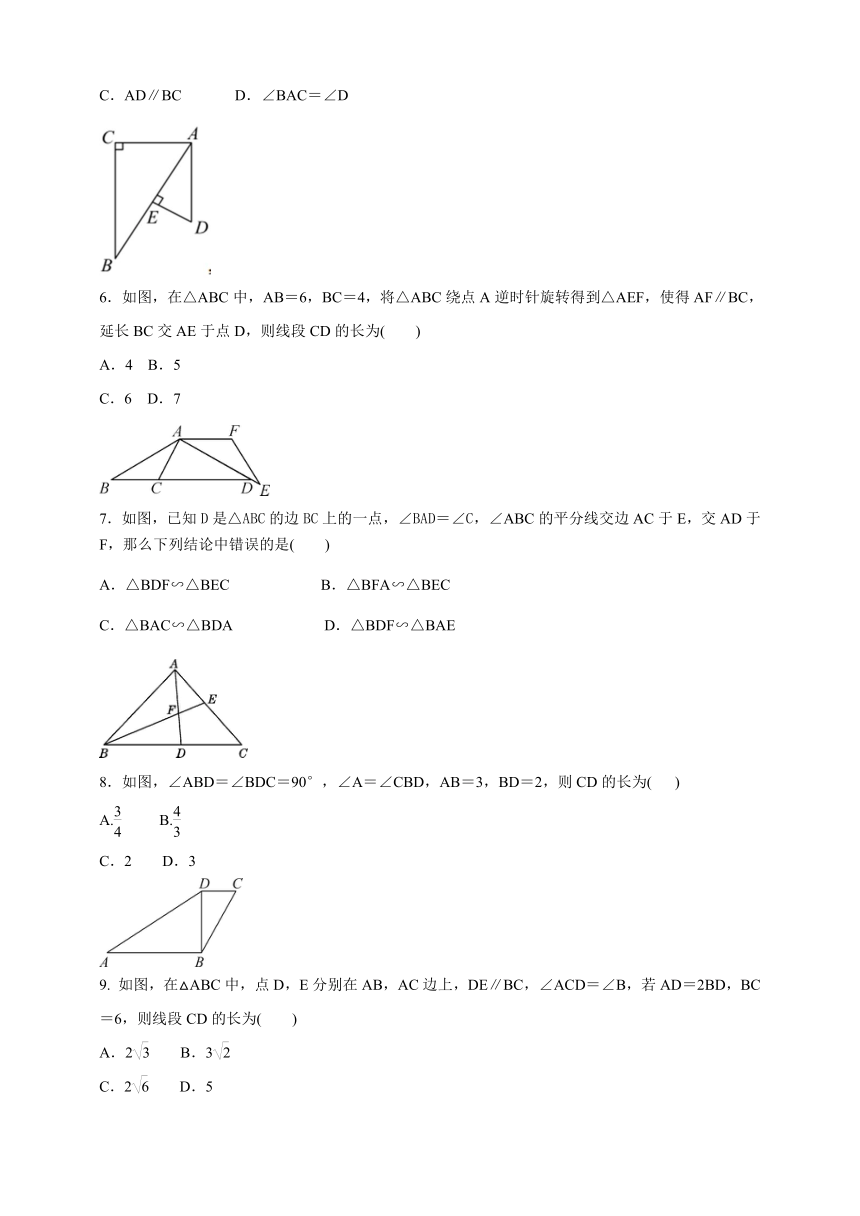
5. 如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍无法判定△ABC∽△DAE的是( )
A.= B.∠B=∠D
C.AD∥BC D.∠BAC=∠D
6.如图,在△ABC中,AB=6,BC=4,将△ABC绕点A逆时针旋转得到△AEF,使得AF∥BC,延长BC交AE于点D,则线段CD的长为( )
A.4 B.5
C.6 D.7
7.如图,已知D是△ABC的边BC上的一点,∠BAD=∠C,∠ABC的平分线交边AC于E,交AD于F,那么下列结论中错误的是( )
A.△BDF∽△BEC B.△BFA∽△BEC
C.△BAC∽△BDA D.△BDF∽△BAE
8.如图,∠ABD=∠BDC=90°,∠A=∠CBD,AB=3,BD=2,则CD的长为( )
A. B.
C.2 D.3
9. 如图,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,∠ACD=∠B,若AD=2BD,BC=6,则线段CD的长为( )
A.2 B.3
C.2 D.5
10. 如图,在菱形ABCD中,已知AB=4,∠ABC=60°,∠EAF=60°,点E在CB的延长线上,点F在DC的延长线上,有下列结论:①BE=CF;②∠EAB=∠CEF;③△ABE∽△EFC;④若∠BAE=15°,则点F到BC的距离为2-2.则其中正确结论的个数是( )
A.1个 B.2个
C.3个 D.4个
二.填空题(共8小题,3*8=24)
11. 如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为________.
12. 如图,已知直角△ABC中,CD是斜边AB上的高,AC=4,BC=3,则AD=_______.
13.如图,在四边形ABCD中,AD∥BC,对角线AC,BD相交于点O,若AO∶CO=2∶3,AD=4,则BC等于_________.
14. 已知正方形ABCD的面积是2,E为正方形一边BC在从B到C方向的延长线上的一点,若CE=,连接AE,与正方形另外一边CD交于点F,连接BF并延长,与线段DE交于点G,则BG的长为________.
15. 如图,在正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为_________.
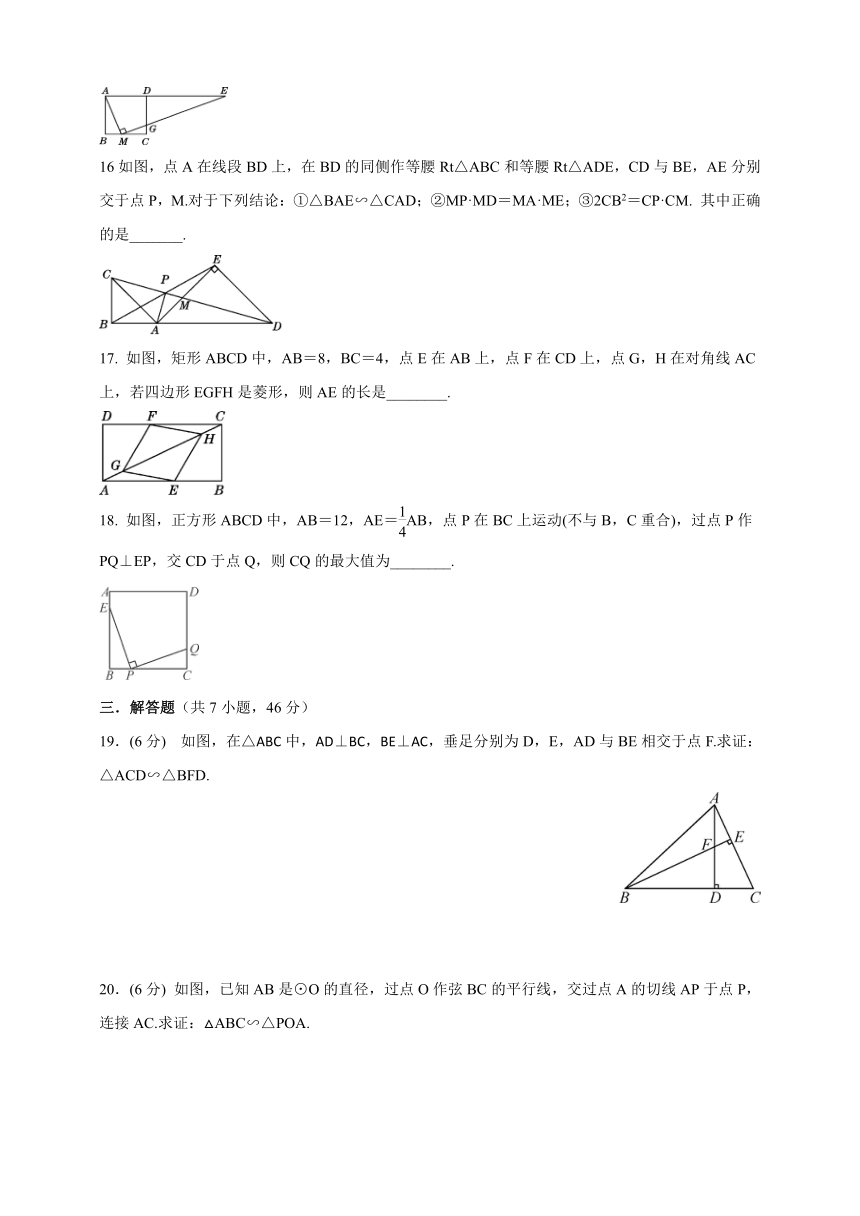
16如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,CD与BE,AE分别交于点P,M.对于下列结论:①△BAE∽△CAD;②MP·MD=MA·ME;③2CB2=CP·CM. 其中正确的是_______.
17. 如图,矩形ABCD中,AB=8,BC=4,点E在AB上,点F在CD上,点G,H在对角线AC上,若四边形EGFH是菱形,则AE的长是________.
18. 如图,正方形ABCD中,AB=12,AE=AB,点P在BC上运动(不与B,C重合),过点P作PQ⊥EP,交CD于点Q,则CQ的最大值为________.
三.解答题(共7小题,46分)
19.(6分) 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.求证:△ACD∽△BFD.
20.(6分) 如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.求证:△ABC∽△POA.
21.(6分) 矩形ABCD中,AB=6,BC=8,点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,求PE的长.
22.(6分) 如图,△ABC内接于⊙O,AC=BC,CD是⊙O的直径,与AB相交于点G,过点D作EF∥AB,分别交CA,CB的延长线于点E,F,连接BD.
(1)求证:EF是⊙O的切线;
(2)求证:BD2=AC·BF.
23.(6分) 如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
24.(8分) 如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D. 求证:(1)△BFD∽△ABD;(2)DE=DB.
25.(8分) 如图,已知AC,AD是⊙O的两条割线,AC与⊙O交于B,C两点,AD过圆心O且与⊙O交于E,D两点,OB平分∠AOC.
(1)求证:△ACD∽△ABO;
(2)过点E的切线交AC于点F,若EF∥OC,OC=3,求EF的值.
参考答案:
1-5 BACAA 6-10 BABCB
11.
12.
13.6
14.
15.
16.①②③
17.5
18. 4
19. 解:∵AD⊥BC,BE⊥AC,∴∠BDF=∠ADC=∠BEC=90°,
∴∠C+∠DBF=90°,∠C+∠DAC=90°,
∴∠DBF=∠DAC,∴△ACD∽△BFD
20. 证明:∵BC∥OP,
∴∠AOP=∠B.
∵AB是直径,∴∠C=90°.
∵PA是⊙O的切线,切点为A,
∴∠OAP=90°,
∴∠C=∠OAP,∴△ABC∽△POA.
21. 如图所示∵四边形ABCD为矩形,∴∠BAD=90°.
∴BD==10.
当PD=DA=8时,BP=BD-PD=2,
∵△PBE∽△DBC,∴=,
即=,解得PE=;
当P′D=P′A时,点P′为BD的中点,
∴P′E′=CD=3.
综上所述,PE的长为或3
22. 解:(1)∵AC=BC,CD是圆的直径,∴由圆的对称性可知:
∠ACD=∠BCD,∴CD⊥AB,∵AB∥EF,∴∠CDF=∠CGB=90°,
∵OD是圆的半径,∴EF是⊙O的切线
(2)∵∠BDF+∠CDB=∠CDB+∠BCD=90°,∴∠BDF=∠BCD,
∴△BCD∽△BDF,∴=,∴BD2=BC·BF,
∵BC=AC,∴BD2=AC·BF
23. 解:(1)∵四边形ABCD是正方形,∴∠B=90°,AD∥BC,
∴∠AMB=∠EAF,又∵EF⊥AM,∴∠AFE=90°,
∴∠B=∠AFE,∴△ABM∽△EFA
(2)∵∠B=90°,AB=12,BM=5,∴AM==13,
AD=12,∵F是AM的中点,∴AF=AM=6.5,∵△ABM∽△EFA,
∴=,即=,∴AE=16.9,∴DE=AE-AD=4.9
24. 证明:(1)∵点E是△ABC的内心,
∴∠BAD=∠CAD.
∵∠CAD=∠CBD,
∴∠BAD=∠CBD.
又∵∠D=∠D,
∴△BFD∽△ABD.
(2)连接BE.
∵点E是△ABC的内心,∴∠ABE=∠CBE.
又∵∠CBD=∠BAD,
∴∠BED=∠BAD+∠ABE=∠CBE+∠CBD=∠DBE.即∠DBE=∠BED,∴DE=DB.
25. 解:(1)∵OB平分∠AOC,∴∠BOE=∠AOC,∵OC=OD,
∴∠D=∠OCD,∵∠AOC=∠D+∠OCD,∴∠D=∠AOC,
∴∠D=∠BOE,且∠A=∠A,∴△ACD∽△ABO
(2)∵EF切⊙O于点E,∴∠OEF=90°,
∵EF∥OC,∴∠DOC=∠OEF=90°,
∵OC=OD=3,∴CD==3,
∵△ACD∽△ABO,∴=,
∴=,∴AE=3,
∵EF∥OC,∴=,
∴=,∴EF=6-3
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
一.选择题(本大题共10小题,每小题3分,共30分)
1.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则下列说法中错误的是( )
A.△ACD∽△CBD B.△ACD∽△ABC
C.△BCD∽△ABC D.△BCD∽△BAC
2.已知一个三角形的两个内角分别是40°,60°,另一个三角形的两个内角分别是40°,80°,则这两个三角形( )
A.一定不相似 B.不一定相似
C.一定相似 D.不能确定
3. 如图,在△ABC中,点D,E分别在AB,AC上,添加下列条件不能判定△AED∽△ABC的是( )
A.∠AED=∠B B.∠ADE=∠C
C.∠ADE=∠B D.=
4.如图,在△ABC中,AE交BC于点D,∠C=∠E,AD∶DE=3∶5,AE=8,BD=4,则DC的长等于( )
A. B. C. D.
5. 如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍无法判定△ABC∽△DAE的是( )
A.= B.∠B=∠D
C.AD∥BC D.∠BAC=∠D
6.如图,在△ABC中,AB=6,BC=4,将△ABC绕点A逆时针旋转得到△AEF,使得AF∥BC,延长BC交AE于点D,则线段CD的长为( )
A.4 B.5
C.6 D.7
7.如图,已知D是△ABC的边BC上的一点,∠BAD=∠C,∠ABC的平分线交边AC于E,交AD于F,那么下列结论中错误的是( )
A.△BDF∽△BEC B.△BFA∽△BEC
C.△BAC∽△BDA D.△BDF∽△BAE
8.如图,∠ABD=∠BDC=90°,∠A=∠CBD,AB=3,BD=2,则CD的长为( )
A. B.
C.2 D.3
9. 如图,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,∠ACD=∠B,若AD=2BD,BC=6,则线段CD的长为( )
A.2 B.3
C.2 D.5
10. 如图,在菱形ABCD中,已知AB=4,∠ABC=60°,∠EAF=60°,点E在CB的延长线上,点F在DC的延长线上,有下列结论:①BE=CF;②∠EAB=∠CEF;③△ABE∽△EFC;④若∠BAE=15°,则点F到BC的距离为2-2.则其中正确结论的个数是( )
A.1个 B.2个
C.3个 D.4个
二.填空题(共8小题,3*8=24)
11. 如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为________.
12. 如图,已知直角△ABC中,CD是斜边AB上的高,AC=4,BC=3,则AD=_______.
13.如图,在四边形ABCD中,AD∥BC,对角线AC,BD相交于点O,若AO∶CO=2∶3,AD=4,则BC等于_________.
14. 已知正方形ABCD的面积是2,E为正方形一边BC在从B到C方向的延长线上的一点,若CE=,连接AE,与正方形另外一边CD交于点F,连接BF并延长,与线段DE交于点G,则BG的长为________.
15. 如图,在正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为_________.
16如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,CD与BE,AE分别交于点P,M.对于下列结论:①△BAE∽△CAD;②MP·MD=MA·ME;③2CB2=CP·CM. 其中正确的是_______.
17. 如图,矩形ABCD中,AB=8,BC=4,点E在AB上,点F在CD上,点G,H在对角线AC上,若四边形EGFH是菱形,则AE的长是________.
18. 如图,正方形ABCD中,AB=12,AE=AB,点P在BC上运动(不与B,C重合),过点P作PQ⊥EP,交CD于点Q,则CQ的最大值为________.
三.解答题(共7小题,46分)
19.(6分) 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.求证:△ACD∽△BFD.
20.(6分) 如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.求证:△ABC∽△POA.
21.(6分) 矩形ABCD中,AB=6,BC=8,点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,求PE的长.
22.(6分) 如图,△ABC内接于⊙O,AC=BC,CD是⊙O的直径,与AB相交于点G,过点D作EF∥AB,分别交CA,CB的延长线于点E,F,连接BD.
(1)求证:EF是⊙O的切线;
(2)求证:BD2=AC·BF.
23.(6分) 如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
24.(8分) 如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D. 求证:(1)△BFD∽△ABD;(2)DE=DB.
25.(8分) 如图,已知AC,AD是⊙O的两条割线,AC与⊙O交于B,C两点,AD过圆心O且与⊙O交于E,D两点,OB平分∠AOC.
(1)求证:△ACD∽△ABO;
(2)过点E的切线交AC于点F,若EF∥OC,OC=3,求EF的值.
参考答案:
1-5 BACAA 6-10 BABCB
11.
12.
13.6
14.
15.
16.①②③
17.5
18. 4
19. 解:∵AD⊥BC,BE⊥AC,∴∠BDF=∠ADC=∠BEC=90°,
∴∠C+∠DBF=90°,∠C+∠DAC=90°,
∴∠DBF=∠DAC,∴△ACD∽△BFD
20. 证明:∵BC∥OP,
∴∠AOP=∠B.
∵AB是直径,∴∠C=90°.
∵PA是⊙O的切线,切点为A,
∴∠OAP=90°,
∴∠C=∠OAP,∴△ABC∽△POA.
21. 如图所示∵四边形ABCD为矩形,∴∠BAD=90°.
∴BD==10.
当PD=DA=8时,BP=BD-PD=2,
∵△PBE∽△DBC,∴=,
即=,解得PE=;
当P′D=P′A时,点P′为BD的中点,
∴P′E′=CD=3.
综上所述,PE的长为或3
22. 解:(1)∵AC=BC,CD是圆的直径,∴由圆的对称性可知:
∠ACD=∠BCD,∴CD⊥AB,∵AB∥EF,∴∠CDF=∠CGB=90°,
∵OD是圆的半径,∴EF是⊙O的切线
(2)∵∠BDF+∠CDB=∠CDB+∠BCD=90°,∴∠BDF=∠BCD,
∴△BCD∽△BDF,∴=,∴BD2=BC·BF,
∵BC=AC,∴BD2=AC·BF
23. 解:(1)∵四边形ABCD是正方形,∴∠B=90°,AD∥BC,
∴∠AMB=∠EAF,又∵EF⊥AM,∴∠AFE=90°,
∴∠B=∠AFE,∴△ABM∽△EFA
(2)∵∠B=90°,AB=12,BM=5,∴AM==13,
AD=12,∵F是AM的中点,∴AF=AM=6.5,∵△ABM∽△EFA,
∴=,即=,∴AE=16.9,∴DE=AE-AD=4.9
24. 证明:(1)∵点E是△ABC的内心,
∴∠BAD=∠CAD.
∵∠CAD=∠CBD,
∴∠BAD=∠CBD.
又∵∠D=∠D,
∴△BFD∽△ABD.
(2)连接BE.
∵点E是△ABC的内心,∴∠ABE=∠CBE.
又∵∠CBD=∠BAD,
∴∠BED=∠BAD+∠ABE=∠CBE+∠CBD=∠DBE.即∠DBE=∠BED,∴DE=DB.
25. 解:(1)∵OB平分∠AOC,∴∠BOE=∠AOC,∵OC=OD,
∴∠D=∠OCD,∵∠AOC=∠D+∠OCD,∴∠D=∠AOC,
∴∠D=∠BOE,且∠A=∠A,∴△ACD∽△ABO
(2)∵EF切⊙O于点E,∴∠OEF=90°,
∵EF∥OC,∴∠DOC=∠OEF=90°,
∵OC=OD=3,∴CD==3,
∵△ACD∽△ABO,∴=,
∴=,∴AE=3,
∵EF∥OC,∴=,
∴=,∴EF=6-3
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
