六年级下册数学单元测试-2.位置 冀教版 (含答案)
文档属性
| 名称 | 六年级下册数学单元测试-2.位置 冀教版 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 123.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-08 15:48:19 | ||
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
六年级下册数学单元测试-2.位置
一、单选题
1.微机课上,笑笑坐在微机教室的第4列第2行,用数对(4,2)表示,明明坐在笑笑正后方的第一个位置上,明明的位置用数对表示是(??? )。
A.?(5,2)?????????????????????????????????B.?(4,3)?????????????????????????????????C.?(3,2)?????????????????????????????????D.?(4,1)
2.数对(3,5)和(3,2)表示的位置是(??? )。
A.?同一列????????????????????????????????????B.?同一行????????????????????????????????????C.?无法确定
3.如图,若将三角形ABC向左平移2格,则顶点A’的位置用数对可以表示为(??? )。
A.?(5,1)???????????????????????????B.?(1,1)???????????????????????????C.?(7,1)???????????????????????????D.?(3,3)
二、判断题
4.小霞在教室的位置用数对表示是(3,4),她在教室的位置是第4行,第3列。
5.将(5,6)向左平移3格后是(5,3)。
6.动物园中熊猫馆的位置是(5,7),说明熊猫馆位置是5列7行。
三、填空题
7.(9,4)表示第________列第________行的位置。(21,7)表示第________列第________行的位置。
8.如右图:A点用数对表示是(1,1),B点用数对表示是(________,________),C点用数对表示是(________,________),三角形ABC是________三角形。
9.小亮在班级的位置是第4列,第3行,用数对表示是________。
10.请用数对表示出图中相关场所的位置。
商业银行________?????????老人院________
11.学校组织同学们去电影院看电影,聪聪的位置用数对表示为(4,5),坐在聪聪正前面的明明的位置是(________?,________),坐在聪聪正后面的乐乐的位置是(________?,________),坐在聪聪左面的笑笑的位置是(________?,________),坐在聪聪右面的淘气的位置是(________?,________)。(列是从聪聪右面第1列开始数的)
四、解答题
12.根据下面的描述,在动物园示意图上标出各个馆的位置,并填空.
①动物园大门位于(5,0),向北走100m,到达熊猫馆(?? , ? ).
②海洋馆位于 (?? , ? )
③大象馆位于(10,3)
④狮虎山到熊猫馆和大象馆的距离相等.
⑤鹿苑位于(1,8),向南走200m,到达猩猩馆;科普馆与这两处距离相等.
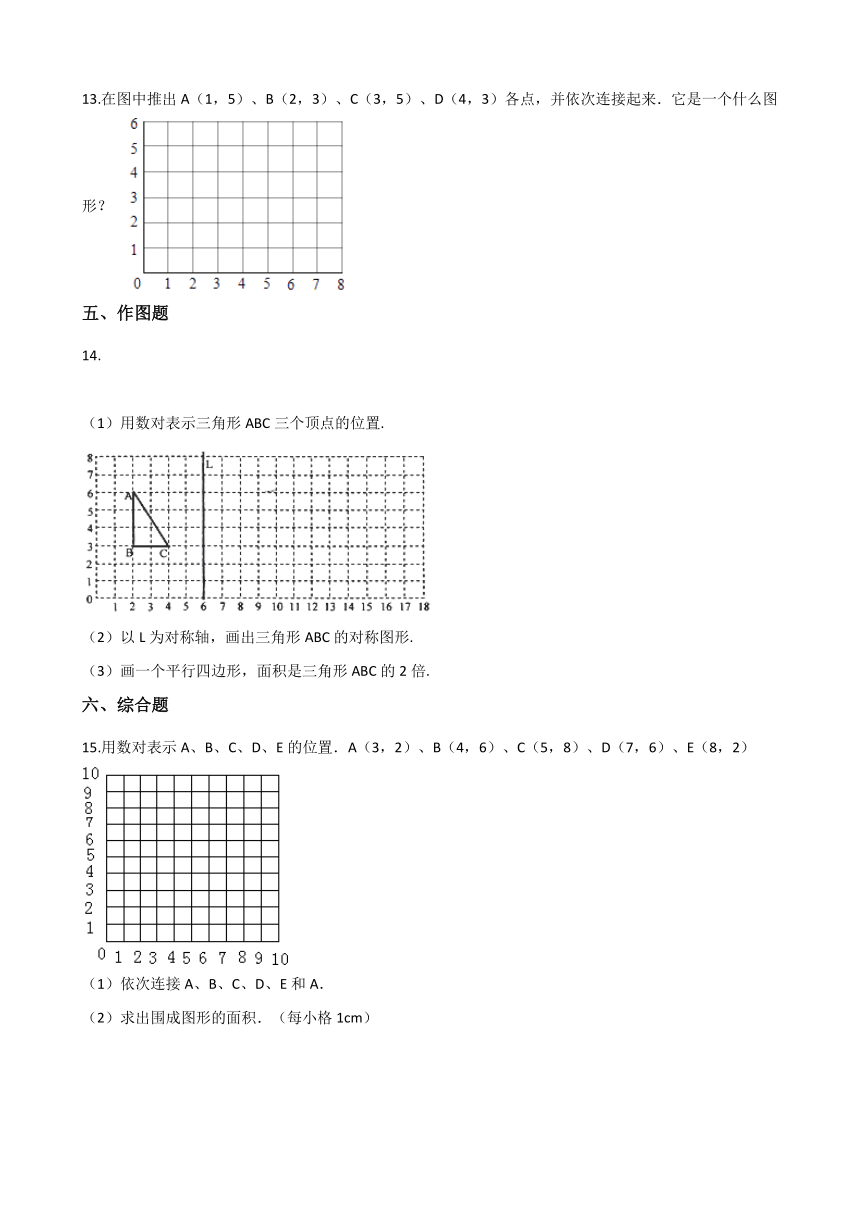
13.在图中推出A(1,5)、B(2,3)、C(3,5)、D(4,3)各点,并依次连接起来.它是一个什么图形?
五、作图题
14.??????????????????????????????
(1)用数对表示三角形ABC三个顶点的位置.
(2)以L为对称轴,画出三角形ABC的对称图形.
(3)画一个平行四边形,面积是三角形ABC的2倍.
六、综合题
15.用数对表示A、B、C、D、E的位置.A(3,2)、B(4,6)、C(5,8)、D(7,6)、E(8,2)
(1)依次连接A、B、C、D、E和A.
(2)求出围成图形的面积.(每小格1cm)
参考答案
一、单选题
1.【答案】 B
【解析】【解答】微机课上,笑笑坐在微机教室的第4列第2行,用数对(4,2)表示,明明坐在笑笑正后方的第一个位置上,明明的位置用数对表示是(4,3).
故答案为:B.
【分析】根据题意可知,明明坐在笑笑正后方的第一个位置上,它们在同一列,明明比笑笑的行数多一行,据此解答即可.
2.【答案】 A
【解析】【解答】(3,5)表示第3列第5行,(3,2)表示第3列第2行,数对(3,5)和(3,2)表示的位置是同一列。
故答案为:A。
【分析】用数对表示位置的方法是:第一个数字表示列,第二个数字表示行,中间用“,”隔开,第一个数字相同,表示同一列,第二个数字相同,表示同一行,据此解答。
3.【答案】 B
【解析】【解答】A’在第1列,第1行,位置用数对可以表示为(1,1)。
故答案为:B
【分析】数对的表示方法:先列后行,即前面的数表示列数,后面的数表示行数。
二、判断题
4.【答案】正确
【解析】【解答】解:她在教师的位置是第4行,第3列,原题说法正确。
故答案为:正确【分析】数对中第一个数表示列,第二个数表示行。由此判断即可。
5.【答案】错误
【解析】【解答】解:将(5,6)向左平移3格后是(2,6),原题说法错误.
故答案为:错误【分析】数对中第一个数表示列,第二个数表示行;向左平移3格,所在的列向左平移3格,所在的行不变.
6.【答案】正确
【解析】【解答】解:动物园中熊猫馆的位置是(5,7),说明熊猫馆位置是第5列第7行,故原题说法正确。
故答案为:正确。
【分析】根据数对表示的意义进行判断即可。
三、填空题
7.【答案】 9;4;21;7
【解析】【解答】 (9,4)表示第9列第4行的位置。(21,7)表示第21列第7行的位置。
故答案为:9;4;21;7。
【分析】用数对表示物体的位置,通常写成(a,b)这种形式,第一个数字a表示在第a列,第二个数字b表示在第b行。
8.【答案】5;1;3;3;等腰
【解析】【解答】解:B点用数对表示是(5,1),C点用数对表示是(3,3),三角形ABC是等腰三角形。
故答案为:5;1;3;3;等腰。【分析】根据点B、C所对应的列与行即可写出它们的位置,根据图示即可得出三角形是等腰三角形。
9.【答案】(4,3)
【解析】【解答】根据用数对表示位置的方法可知,小亮的位置用数对表示是(4,3).
故答案为:(4,3)
【分析】数对中第一个数表示列,第二个数表示行,两个数字中间用逗号隔开,用括号括住两个数字即可.
10.【答案】3,5;5,2
【解析】【解答】解:观察图形,根据数对表示位置的方法可知:商业银行的位置是:(3,5);老人院的位置是:(5,2).故答案为:(3,5);(5,2).
【分析】数对中第一个数表示列,第二个数表示行,由此判断出所在的列与行并用数对表示出来即可.
11.【答案】4;4;4;6;5;5;3;5
【解析】【解答】根据分析可知,聪聪的位置用数对表示为(4,5),坐在聪聪正前面的明明的位置是(4,4),坐在聪聪正后面的乐乐的位置是(4,6),坐在聪聪左面的笑笑的位置是(?5,5),坐在聪聪右面的淘气的位置是(3,5)。
故答案为:4,4;4,6;5,5;3,5.
【分析】根据条件“列是从聪聪右面第1列开始数的”可知,坐在聪聪正前面的明明与聪聪在同一列,只是行数少1,坐在聪聪正后面的乐乐与聪聪在同一列,只是行数多1;因为列数是从右向左数的,所以聪聪左面的笑笑的列数要比聪聪多1列,坐在聪聪右面的淘气的列数要比聪聪少1列,据此解答.
四、解答题
12.【答案】 解:①(5,2);② (9,9)
根据题干,可在平面图中将各个馆的位置标出来,如下图所示:
熊猫馆的位置为:(5,2),
海洋馆的位置为:(9,9),
狮虎山的位置为:(7,5),
猩猩馆的位置为:(1,4),
科普馆的位置为:(2,6).
【解析】【分析】用数对表示位置时,第一个数表示第几列,第二个数表示第几行.由此即可标出图中各个馆的位置.此题考查了用数对表示物体位置的方法.
13.【答案】解:作图如下:
依次连接起来组成2个三角形
【解析】【分析】根据在数对中的第一个数表示列数,第二个数表示行数,在图中分别找出对应的点,并顺次连接A,B,C,D,观察所围成的图形即可得出答案.
五、作图题
14.【答案】(1)解:根据数对表示位置的方法表示出三角形的三个顶点的数对位置分别是:A是(2,6);B是(2,3);C是(4,3)
(2)解:从三角形的三个顶点向直线L引垂线并延长相同长度,找到对应点,顺次连接即可得出三角形ABC的轴对称图形如图所示
(3)解:假设每个小格表示1,则三角形的面积是:2×3÷2=3,
所以平行四边形的面积是3×2=6,以3为底,2为高即可画出这个平行四边形如图所示:
【解析】【分析】用有顺序的两个数表示出一个确定的位置就是谁对,用数对表示位置时,先表示第几列,再表示第几行.
六、综合题
15.【答案】 (1)解:(1)根据数对表示位置的方法,在平面图中标出点A、B、C、D、E,并依次连接起来得出一个封闭的不规则图形如图所示;
(2)解:连接BD,则把这个不规则的图形分成了两部分:底为3厘米高为2厘米的三角形和上下底分别是3厘米、5厘米,高是4厘米的梯形,则这个图形的面积是:
3×2÷2+(3+5)×4÷2,
=3+16,
=19(平方厘米),
答:这个图形的面积是19平方厘米.
【解析】【分析】(1)数对表示位置的方法是:第一个数字表示列,第二个数字表示行,由此即可在平面图中标出点A、B、C、D、E,并依次连接起来得出一个封闭的不规则图形;(2)连接BD,则把这个不规则的图形分成了两部分:底为3厘米高为2厘米的三角形和上下底分别是3厘米、5厘米,高是4厘米的梯形,由此利用三角形和图形的面积公式即可解答.此题考查了数对表示位置的方法和根据方格图,利用三角形和梯形的面积公式求组合图形的面积的灵活应用.
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
六年级下册数学单元测试-2.位置
一、单选题
1.微机课上,笑笑坐在微机教室的第4列第2行,用数对(4,2)表示,明明坐在笑笑正后方的第一个位置上,明明的位置用数对表示是(??? )。
A.?(5,2)?????????????????????????????????B.?(4,3)?????????????????????????????????C.?(3,2)?????????????????????????????????D.?(4,1)
2.数对(3,5)和(3,2)表示的位置是(??? )。
A.?同一列????????????????????????????????????B.?同一行????????????????????????????????????C.?无法确定
3.如图,若将三角形ABC向左平移2格,则顶点A’的位置用数对可以表示为(??? )。
A.?(5,1)???????????????????????????B.?(1,1)???????????????????????????C.?(7,1)???????????????????????????D.?(3,3)
二、判断题
4.小霞在教室的位置用数对表示是(3,4),她在教室的位置是第4行,第3列。
5.将(5,6)向左平移3格后是(5,3)。
6.动物园中熊猫馆的位置是(5,7),说明熊猫馆位置是5列7行。
三、填空题
7.(9,4)表示第________列第________行的位置。(21,7)表示第________列第________行的位置。
8.如右图:A点用数对表示是(1,1),B点用数对表示是(________,________),C点用数对表示是(________,________),三角形ABC是________三角形。
9.小亮在班级的位置是第4列,第3行,用数对表示是________。
10.请用数对表示出图中相关场所的位置。
商业银行________?????????老人院________
11.学校组织同学们去电影院看电影,聪聪的位置用数对表示为(4,5),坐在聪聪正前面的明明的位置是(________?,________),坐在聪聪正后面的乐乐的位置是(________?,________),坐在聪聪左面的笑笑的位置是(________?,________),坐在聪聪右面的淘气的位置是(________?,________)。(列是从聪聪右面第1列开始数的)
四、解答题
12.根据下面的描述,在动物园示意图上标出各个馆的位置,并填空.
①动物园大门位于(5,0),向北走100m,到达熊猫馆(?? , ? ).
②海洋馆位于 (?? , ? )
③大象馆位于(10,3)
④狮虎山到熊猫馆和大象馆的距离相等.
⑤鹿苑位于(1,8),向南走200m,到达猩猩馆;科普馆与这两处距离相等.
13.在图中推出A(1,5)、B(2,3)、C(3,5)、D(4,3)各点,并依次连接起来.它是一个什么图形?
五、作图题
14.??????????????????????????????
(1)用数对表示三角形ABC三个顶点的位置.
(2)以L为对称轴,画出三角形ABC的对称图形.
(3)画一个平行四边形,面积是三角形ABC的2倍.
六、综合题
15.用数对表示A、B、C、D、E的位置.A(3,2)、B(4,6)、C(5,8)、D(7,6)、E(8,2)
(1)依次连接A、B、C、D、E和A.
(2)求出围成图形的面积.(每小格1cm)
参考答案
一、单选题
1.【答案】 B
【解析】【解答】微机课上,笑笑坐在微机教室的第4列第2行,用数对(4,2)表示,明明坐在笑笑正后方的第一个位置上,明明的位置用数对表示是(4,3).
故答案为:B.
【分析】根据题意可知,明明坐在笑笑正后方的第一个位置上,它们在同一列,明明比笑笑的行数多一行,据此解答即可.
2.【答案】 A
【解析】【解答】(3,5)表示第3列第5行,(3,2)表示第3列第2行,数对(3,5)和(3,2)表示的位置是同一列。
故答案为:A。
【分析】用数对表示位置的方法是:第一个数字表示列,第二个数字表示行,中间用“,”隔开,第一个数字相同,表示同一列,第二个数字相同,表示同一行,据此解答。
3.【答案】 B
【解析】【解答】A’在第1列,第1行,位置用数对可以表示为(1,1)。
故答案为:B
【分析】数对的表示方法:先列后行,即前面的数表示列数,后面的数表示行数。
二、判断题
4.【答案】正确
【解析】【解答】解:她在教师的位置是第4行,第3列,原题说法正确。
故答案为:正确【分析】数对中第一个数表示列,第二个数表示行。由此判断即可。
5.【答案】错误
【解析】【解答】解:将(5,6)向左平移3格后是(2,6),原题说法错误.
故答案为:错误【分析】数对中第一个数表示列,第二个数表示行;向左平移3格,所在的列向左平移3格,所在的行不变.
6.【答案】正确
【解析】【解答】解:动物园中熊猫馆的位置是(5,7),说明熊猫馆位置是第5列第7行,故原题说法正确。
故答案为:正确。
【分析】根据数对表示的意义进行判断即可。
三、填空题
7.【答案】 9;4;21;7
【解析】【解答】 (9,4)表示第9列第4行的位置。(21,7)表示第21列第7行的位置。
故答案为:9;4;21;7。
【分析】用数对表示物体的位置,通常写成(a,b)这种形式,第一个数字a表示在第a列,第二个数字b表示在第b行。
8.【答案】5;1;3;3;等腰
【解析】【解答】解:B点用数对表示是(5,1),C点用数对表示是(3,3),三角形ABC是等腰三角形。
故答案为:5;1;3;3;等腰。【分析】根据点B、C所对应的列与行即可写出它们的位置,根据图示即可得出三角形是等腰三角形。
9.【答案】(4,3)
【解析】【解答】根据用数对表示位置的方法可知,小亮的位置用数对表示是(4,3).
故答案为:(4,3)
【分析】数对中第一个数表示列,第二个数表示行,两个数字中间用逗号隔开,用括号括住两个数字即可.
10.【答案】3,5;5,2
【解析】【解答】解:观察图形,根据数对表示位置的方法可知:商业银行的位置是:(3,5);老人院的位置是:(5,2).故答案为:(3,5);(5,2).
【分析】数对中第一个数表示列,第二个数表示行,由此判断出所在的列与行并用数对表示出来即可.
11.【答案】4;4;4;6;5;5;3;5
【解析】【解答】根据分析可知,聪聪的位置用数对表示为(4,5),坐在聪聪正前面的明明的位置是(4,4),坐在聪聪正后面的乐乐的位置是(4,6),坐在聪聪左面的笑笑的位置是(?5,5),坐在聪聪右面的淘气的位置是(3,5)。
故答案为:4,4;4,6;5,5;3,5.
【分析】根据条件“列是从聪聪右面第1列开始数的”可知,坐在聪聪正前面的明明与聪聪在同一列,只是行数少1,坐在聪聪正后面的乐乐与聪聪在同一列,只是行数多1;因为列数是从右向左数的,所以聪聪左面的笑笑的列数要比聪聪多1列,坐在聪聪右面的淘气的列数要比聪聪少1列,据此解答.
四、解答题
12.【答案】 解:①(5,2);② (9,9)
根据题干,可在平面图中将各个馆的位置标出来,如下图所示:
熊猫馆的位置为:(5,2),
海洋馆的位置为:(9,9),
狮虎山的位置为:(7,5),
猩猩馆的位置为:(1,4),
科普馆的位置为:(2,6).
【解析】【分析】用数对表示位置时,第一个数表示第几列,第二个数表示第几行.由此即可标出图中各个馆的位置.此题考查了用数对表示物体位置的方法.
13.【答案】解:作图如下:
依次连接起来组成2个三角形
【解析】【分析】根据在数对中的第一个数表示列数,第二个数表示行数,在图中分别找出对应的点,并顺次连接A,B,C,D,观察所围成的图形即可得出答案.
五、作图题
14.【答案】(1)解:根据数对表示位置的方法表示出三角形的三个顶点的数对位置分别是:A是(2,6);B是(2,3);C是(4,3)
(2)解:从三角形的三个顶点向直线L引垂线并延长相同长度,找到对应点,顺次连接即可得出三角形ABC的轴对称图形如图所示
(3)解:假设每个小格表示1,则三角形的面积是:2×3÷2=3,
所以平行四边形的面积是3×2=6,以3为底,2为高即可画出这个平行四边形如图所示:
【解析】【分析】用有顺序的两个数表示出一个确定的位置就是谁对,用数对表示位置时,先表示第几列,再表示第几行.
六、综合题
15.【答案】 (1)解:(1)根据数对表示位置的方法,在平面图中标出点A、B、C、D、E,并依次连接起来得出一个封闭的不规则图形如图所示;
(2)解:连接BD,则把这个不规则的图形分成了两部分:底为3厘米高为2厘米的三角形和上下底分别是3厘米、5厘米,高是4厘米的梯形,则这个图形的面积是:
3×2÷2+(3+5)×4÷2,
=3+16,
=19(平方厘米),
答:这个图形的面积是19平方厘米.
【解析】【分析】(1)数对表示位置的方法是:第一个数字表示列,第二个数字表示行,由此即可在平面图中标出点A、B、C、D、E,并依次连接起来得出一个封闭的不规则图形;(2)连接BD,则把这个不规则的图形分成了两部分:底为3厘米高为2厘米的三角形和上下底分别是3厘米、5厘米,高是4厘米的梯形,由此利用三角形和图形的面积公式即可解答.此题考查了数对表示位置的方法和根据方格图,利用三角形和梯形的面积公式求组合图形的面积的灵活应用.
