人教版七年级下册数学7.2.2用坐标表示平移课件(共30张PPT)
文档属性
| 名称 | 人教版七年级下册数学7.2.2用坐标表示平移课件(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 840.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-06 21:52:53 | ||
图片预览









文档简介
(共30张PPT)
7.2 坐标方法的简单应用/
人教版
数学 七年级 下册
7.2
坐标方法的简单应用
7.2.2
用坐标表示平移
导入新知
7.2 坐标方法的简单应用/
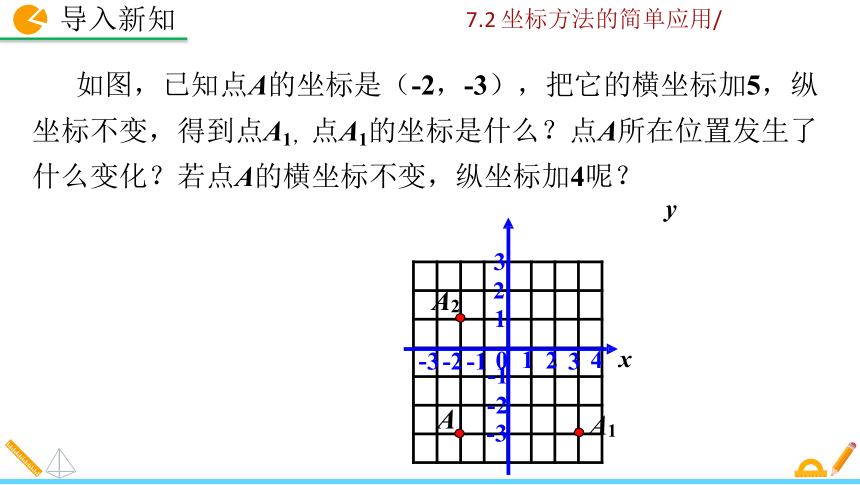
如图,已知点A的坐标是(-2,-3),把它的横坐标加5,纵
坐标不变,得到点A1,点A1的坐标是什么?点A所在位置发生了
什么变化?若点A的横坐标不变,纵坐标加4呢?
y
3
A2
1
x
1
4
3 -2 -1
0
2
3
-1
-2
A1
-3
2
-
A
素养目标
7.2 坐标方法的简单应用/
1. 掌握坐标变化与图形平移的关系,能利用点 的平移规律将平面图形进行平移 .
2. 会根据图形上点的坐标的变化,来判定图形 的移动过程.
3.体会平面直角坐标系是数与形之间的桥梁,感 受代数与几何的相互转化,初步建立空间概念.
探究新知
7.2 坐标方法的简单应用/
知识点 1
平面直角坐标系点的移动
y
如图,将点A(-2,-3)向右平
移5个单位长度,得到点A ,
1
在图上标出这个点,写出坐标.
将点A(-2,-3)向上平移4个单位
长度呢?将点A向左或向下平
移,观察它们的坐标变化,你
能从中发现什么规律吗?
再找几个点,进行平移, 它们的坐标是否按照你的规律
-3
-2
-1
1
2
x
1
2
3
2,-3)
(3,-3)
-4
变化.
4
3
A
2(-2
,1)
2
1
-4
O
3
4
-
-
A(-
-
A1
探究新知
7.2 坐标方法的简单应用/
归纳总结
在平面直角坐标系中,将点(x,y)向右(或
左)平移a个单位长度,可以得到对应点(x+a,y)
(或(_x-_a , _y_ ));将点(x,y)向上(或下)
平移b个单位长度,可以得到对应点(x,y+b)
(或(_x _, _y-_b )).
探究新知
7.2 坐标方法的简单应用/
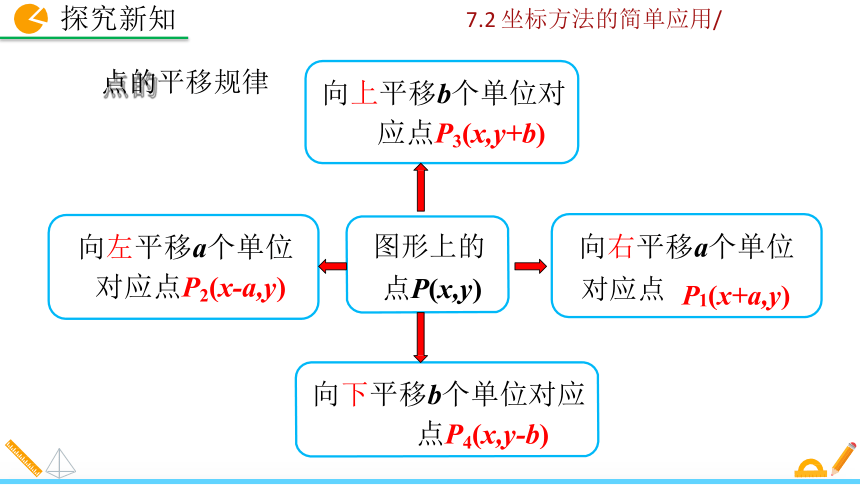
点的平移规律
向上平移b个单位对
应点P3(x,y+b)
向左平移a个单位
对应点P2(x-a,y)
向右平移a个单位
图形上的
点P(x,y)
对应点
P1(x+a,y)
向下平移b个单位对应
点P4(x,y-b)
探究新知
7.2 坐标方法的简单应用/
平面直角坐标系内点的平移
素养考点
1
例1
平面直角坐标系中,将点A(-3,-5)向上平移4个单位,再
向左平移3个单位到点B,则点B的坐标为(
)
C
A.(1,-8)
B.(1,-2)
C.(-6,-1)
D.(0,-1)
解析:点A的坐标为(-3,-5),将点A向上平移4个单位,再向
左平移3个单位到点B,点B的横坐标是-3-3=-6,纵坐标 为-5+4=-1,即(-6,-1).
;
上下移动改变点的纵坐标,下减上加.
提示:点的平移变换:左右移动改变点的横坐标,左减右加
巩固练习
7.2 坐标方法的简单应用/
1.根据平移填空.
①将点(2,1)向右平移3个单位长度,
_(5_,_1_)
可以得到对应点坐标_
_
;
②将点(2,-1)向左平移3个单位长度,
(_-1_,_-_1_) __
可以得到对应点坐标_
;
③将点(2,5)向上平移3个单位长度,
_(2_,_8_)
可以得到对应点坐标_
_
;
④将点(-2,5)向下平移3单位长度,
_(-_2_,2_)
可以得到对应点坐标_
_.
探究新知
7.2 坐标方法的简单应用/
知识点 2
平面直角坐标系内图形的平移
问题1:如图,三角形ABC三个顶点的坐标分别是:A(4,3),
B(3,1),C(1,2).
(1)将三角形ABC三个顶点的 横坐标都减去6,纵坐标不变, 分别得到点A1,B1,C1,点A1, B1 ,C1坐标分别是什么?并画出 相应的三角形A1B1C1 .
探究新知
7.2 坐标方法的简单应用/
问题1:如图,三角形ABC三个顶点的坐标分别是:A(4,3),
B(3,1),C(1,2).
(2)三角形A1B1C1与三角形ABC
的大小、形状和位置上有什么关
系,为什么?
(3)若三角形ABC三个顶点的横 坐标都加5,纵坐标不变呢?
探究新知
7.2 坐标方法的简单应用/
解: A1(-2,3),B1(-3,1),C1(-5,2),即三角形
ABC向左平移了6个单位长度,因此所得三角形A1B1C1与三角
形ABC的大小、形状完全相同.
用类比的思想,把三角形ABC
三个顶点的横坐标都加5,纵
坐标不变,即三角形ABC向右
平移了5个单位长度,因此所
得三角形与三角形ABC的大小、
形状完全相同.
探究新知
7.2 坐标方法的简单应用/
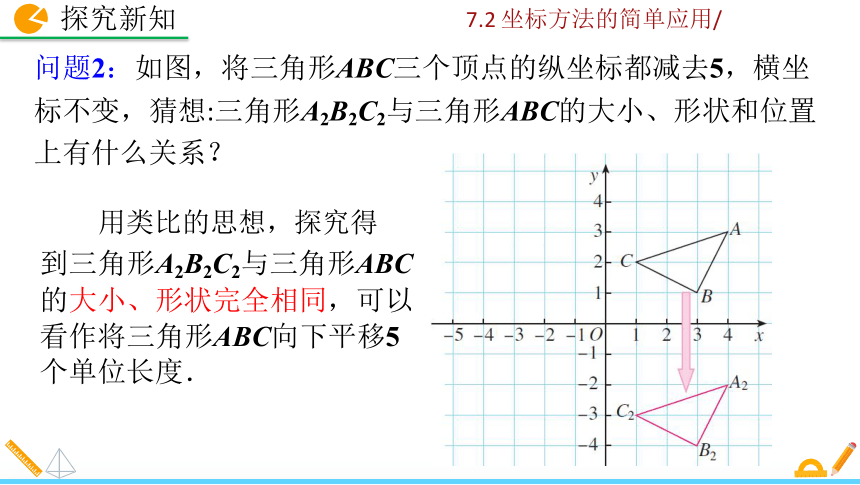
问题2:如图,将三角形ABC三个顶点的纵坐标都减去5,横坐
标不变,猜想:三角形A2B2C2与三角形ABC的大小、形状和位置 上有什么关系?
用类比的思想,探究得
到三角形A2B2C2与三角形ABC
的大小、形状完全相同,可以
看作将三角形ABC向下平移5
个单位长度.
探究新知
7.2 坐标方法的简单应用/
问题3:如图,将三角形ABC三个顶点的横坐标都减去
同时纵坐标减去5,又能得到什么结论?
将三角形ABC三个顶点的
横坐标都减去 6,同时纵坐标
减去5,分别得到点的坐标是
(-2,-2),( -5,-3 ),
(-3,-4 ),依次连接这三点,
可以发现所得三角形可以由三
角形ABC先向左平移6个单位
长度,再向下平移5个单位长
度得到.三角形的大小、形状
6,
完全相同.
探究新知
7.2 坐标方法的简单应用/
问题4:如图所示,正方形ABCD四个顶点的坐标分别是A(-2,
4),B(-2,3),C(-1,3),D(-1,4),将正方形ABCD 向下平移7个单位长度,再向右平移8个单位长度,两次平移后 四个顶点相应变为点E,F,G,H.
(1)点E,F,G,H的坐标分别是什么?
探究新知
7.2 坐标方法的简单应用/
问题4:如图所示,正方形ABCD四个顶点的坐标分别是A(-2,
4),B(-2,3),C(-1,3),D(-1,4),将正方形
ABCD向下平移7个单位长度,再向右平移8个单位长度,两次 平移后四个顶点相应变为点E,F,G,H.
(2)如果直接平移正方形ABCD,使点A移到点E,它和我们
前面得到的正方形位置相同吗?
探究新知
7.2 坐标方法的简单应用/
点E,F,G,H的坐标分别是:(6,-3),(6,-4),
(7,-4),(7,-3).若直接平移正方形ABCD,使点A
移到点E,它就和我们前面得到的正方形位置相同.
探究新知
7.2 坐标方法的简单应用/
问题5:通过前面问题的探究,你能总结图形上点的坐标的某
种变化引起了图形怎样的平移吗?
在平面直角坐标系内,如果把一个图形各个点的横坐标
都加(或减去)一个正数a,相应的新图形就是把原图形向右
(或向左)平移a个单位长度;如果把它各个点的纵坐标都加
(或减去)一个正数b,相应的新图形就是把原图形向上(或 向下)平移b个单位长度.
探究新知
7.2 坐标方法的简单应用/
1
2
归纳总结
(1)原图形向右(左)平移a个单位长度:(a>0)
原图形上的点P(x,y) 向右平移a个单位 P (x+a,y)
原图形上的点P (x,y) 向左平移a个单位 P (x-a,y)
(2)原图形向上(下)平移b个单位长度:(b>0)
原图形上的点P(x,y) 向上平移b个单位 P3(x,y+b)
原图形上的点P(x,y) 向下平移b个单位 P4(x,y-b)
探究新知
7.2 坐标方法的简单应用/
平面直角坐标系内图形的平移
素养考点
1
例2 如图,在平面直角坐标系中,P(a,b)是三角形ABC的边AC上
一点,三角形ABC经平移后点P的对应点为P1(a+6,b+2).
y
(1)请画出上述平移后的三角
形A1B1C1,并写出点A、C、
A1、C1的坐标;
A1
P1
1
P
1
B
1
解:(1)三角形A1B1C1如图所示,
各点的坐标分别为A(-3,2)、
C
x
C(-2,0)、A1(3,4)、C1(4,2);
A
B
C
1
C
O
探究新知
7.2 坐标方法的简单应用/
(2)
求出以A、C、A1、C1为顶点的四边形的面积.
y
A1
解:(2)连接AA1,CC1,
A
B1
S四边形ACC A
1 1
=
SΔAA C + SΔAC C
1 1 1
P
B
1
1
?? ? 2 ? 7 ? 7 ? S ΔAC C
S ΔAA C
1
x
2
=
O
1 1
1
∴S四边形ACC A
1 1
SΔAA C
1 1
+ SΔAC C =14.
1
P
1
C
1
C
探究新知
7.2 坐标方法的简单应用/
一个图形依次沿x轴方向、y轴方向平移后所得图形与原来
的图形相比,位置有什么变化?它们对应点的坐标之间有怎样
的关系?
平移方向和平移距离
对应点的坐标
向右平移a个单位长度,向上平移b个单位长度
(x+a , y+b)
向右平移a个单位长度,向下平移b个单位长度
(x+a , y-b)
向左平移a个单位长度,向上平移b个单位长度
(x-a , y+b)
向左平移a个单位长度,向下平移b个单位长度
(x-a , y-b)
巩固练习
7.2 坐标方法的简单应用/
2.如图,将平行四边形ABCD向左
平移2个单位长度,然后再向上平 移3个单位长度,可以得到平行四 边形A'B'C'D',画出平移后 的图形,并指出其各个顶点的坐标.
D′
C′
A′
B′
解:如图所示,四边形A′B′C′D′就是所要画的四边形,
A′(-3,1), B′(1,1), C′(2,4), D′(-2,4).
巩固练习
7.2 坐标方法的简单应用/
连 接 中 考
1.(2019?大连)在平面直角坐标系中,将点P(3,1)向下平移
A
2个单位长度,得到的点P′的坐标为(
)
A.(3,﹣1) B.(3,3)
C.(1,1) D.(5,1)
2.(2019?海南)如图,在平面直角坐标系中,已知点A(2,1),
点B(3,-1),平移线段AB,使点A落在点A1(-2,2)处,则
点B的对应点B1的坐标为(
)
C
A.(-1,-1)
C.(-1,0)
B.(1,0)
D.(3,0)
课堂检测
7.2 坐标方法的简单应用/
基
础
巩 固
题
1.(1)如图所示,将点A向右平移(
B )个单位长度可得到点B .
C.5个单位长度 D.6个单位长度
A.3个单位长度
B. 4个单位长度
(2)如图所示,将点A向下平移5个单位长度后,将重合于图中的
y
(
).
4
3
2
1
D
A
B
A.点C
C.点D
B.点F
D.点E
-4
-3 -2 -1 0
1
2 3 4
x
C
-1
D E
-2
G -3
F -4
课堂检测
7.2 坐标方法的简单应用/
基
础
巩
固
题
(3)如图所示,点G(-2,-2),将点G先向右平移6个单位长度,再
向上平移5个单位长度,得到G′,则G′的坐标为(
D ).
A.(6,5)
B.(4,5)
C.(6,3)
D.(4,3)
y
4
3
2
1
A
B
-3 -2 -1 0
-4
1 2 3
4
x
C
-1
D E
-2
G -3
F -4
课堂检测
7.2 坐标方法的简单应用/
基
础
巩
固
题
(4)如图所示,将点A先向右平移3个单位长度,再向下平移5个
单位长度,得到A′为 _( 0_,__-3_)_;将点B先向下平移5个单位长
度,再向右平移3个单位长度,得到B′为(__4_,
相距 _4_个单位长度.
-_3_)_,则A′与B′
y
4
3
2
1
A
B
-4
-3 -2 -1 0
1 2 3 4
x
C
-1
D E
-2
G -3
F -4
课堂检测
7.2 坐标方法的简单应用/
基
础
巩
固
题
2.把一个图形上的各点的横坐标都减去1,再把它的各点的纵坐
标都加上2,则这个图形的平移方式是__先__向__左__平
__再 向 上 平 移 2_个__单__位_ .
移
1_个__单__位__,__
3.点P(a,b)向左平移1个单位长度,再向上平移1个单位长
度,得到点(3,-4),则a=__4__,b= _-_5
.
课堂检测
7.2 坐标方法的简单应用/
能
力
提
升
题
1.已知线段
MN=4,MN∥y轴,若点M坐标为(-1,2),则N点
坐标为(__-1_, -_2_) 或 ( -_1_,__6_) ;
2.已知线段 MN=4,MN∥x轴,若点M坐标为(-1,2),则N点坐
标为 ( 3_,__2_) 或 ( -5_, 2_)_.
B
-
1
-
1
2
1
3
-
-
2
4
5
4
3
2
-
-
-
-
C
2
1
4
3
课堂检测
7.2 坐标方法的简单应用/
y
拓
广
探
索
题
A1
如图,三角形ABC上任
意一点P(x0,y0)经平移后得
B1
,2)
x
+2,y
+4)
C (3,0
O
x
到的对应点为P1(x0+2,y0+4),
)
)B
将三角形ABC作同样的平
移得到三角形A1B1C1.求A1、
B1、C1的坐标.
解:A(-3,2)经平移后得到(-3+2,2+4),即A1(-1,6);B(-2,-1)
经平移后得到(-2+2,-1+4),即B1(0,3);C(3,0)经平移后得到
(3+2,0+4),即C1(5,4).
C1
(
-3
A
P
1(
0
0
)
(
-2,
-13
P
(x
0,
y0
课堂小结
7.2 坐标方法的简单应用/
向下平移,纵坐标减去一个正数
沿y轴平移
向上平移,纵坐标加上一个正数
横坐标不变
图形在坐标
系中的平移
向左平移,横坐标减去一个正数
沿x轴平移
向右平移,横坐标加上一个正数
纵坐标不变
7.2 坐标方法的简单应用/
人教版
数学 七年级 下册
7.2
坐标方法的简单应用
7.2.2
用坐标表示平移
导入新知
7.2 坐标方法的简单应用/
如图,已知点A的坐标是(-2,-3),把它的横坐标加5,纵
坐标不变,得到点A1,点A1的坐标是什么?点A所在位置发生了
什么变化?若点A的横坐标不变,纵坐标加4呢?
y
3
A2
1
x
1
4
3 -2 -1
0
2
3
-1
-2
A1
-3
2
-
A
素养目标
7.2 坐标方法的简单应用/
1. 掌握坐标变化与图形平移的关系,能利用点 的平移规律将平面图形进行平移 .
2. 会根据图形上点的坐标的变化,来判定图形 的移动过程.
3.体会平面直角坐标系是数与形之间的桥梁,感 受代数与几何的相互转化,初步建立空间概念.
探究新知
7.2 坐标方法的简单应用/
知识点 1
平面直角坐标系点的移动
y
如图,将点A(-2,-3)向右平
移5个单位长度,得到点A ,
1
在图上标出这个点,写出坐标.
将点A(-2,-3)向上平移4个单位
长度呢?将点A向左或向下平
移,观察它们的坐标变化,你
能从中发现什么规律吗?
再找几个点,进行平移, 它们的坐标是否按照你的规律
-3
-2
-1
1
2
x
1
2
3
2,-3)
(3,-3)
-4
变化.
4
3
A
2(-2
,1)
2
1
-4
O
3
4
-
-
A(-
-
A1
探究新知
7.2 坐标方法的简单应用/
归纳总结
在平面直角坐标系中,将点(x,y)向右(或
左)平移a个单位长度,可以得到对应点(x+a,y)
(或(_x-_a , _y_ ));将点(x,y)向上(或下)
平移b个单位长度,可以得到对应点(x,y+b)
(或(_x _, _y-_b )).
探究新知
7.2 坐标方法的简单应用/
点的平移规律
向上平移b个单位对
应点P3(x,y+b)
向左平移a个单位
对应点P2(x-a,y)
向右平移a个单位
图形上的
点P(x,y)
对应点
P1(x+a,y)
向下平移b个单位对应
点P4(x,y-b)
探究新知
7.2 坐标方法的简单应用/
平面直角坐标系内点的平移
素养考点
1
例1
平面直角坐标系中,将点A(-3,-5)向上平移4个单位,再
向左平移3个单位到点B,则点B的坐标为(
)
C
A.(1,-8)
B.(1,-2)
C.(-6,-1)
D.(0,-1)
解析:点A的坐标为(-3,-5),将点A向上平移4个单位,再向
左平移3个单位到点B,点B的横坐标是-3-3=-6,纵坐标 为-5+4=-1,即(-6,-1).
;
上下移动改变点的纵坐标,下减上加.
提示:点的平移变换:左右移动改变点的横坐标,左减右加
巩固练习
7.2 坐标方法的简单应用/
1.根据平移填空.
①将点(2,1)向右平移3个单位长度,
_(5_,_1_)
可以得到对应点坐标_
_
;
②将点(2,-1)向左平移3个单位长度,
(_-1_,_-_1_) __
可以得到对应点坐标_
;
③将点(2,5)向上平移3个单位长度,
_(2_,_8_)
可以得到对应点坐标_
_
;
④将点(-2,5)向下平移3单位长度,
_(-_2_,2_)
可以得到对应点坐标_
_.
探究新知
7.2 坐标方法的简单应用/
知识点 2
平面直角坐标系内图形的平移
问题1:如图,三角形ABC三个顶点的坐标分别是:A(4,3),
B(3,1),C(1,2).
(1)将三角形ABC三个顶点的 横坐标都减去6,纵坐标不变, 分别得到点A1,B1,C1,点A1, B1 ,C1坐标分别是什么?并画出 相应的三角形A1B1C1 .
探究新知
7.2 坐标方法的简单应用/
问题1:如图,三角形ABC三个顶点的坐标分别是:A(4,3),
B(3,1),C(1,2).
(2)三角形A1B1C1与三角形ABC
的大小、形状和位置上有什么关
系,为什么?
(3)若三角形ABC三个顶点的横 坐标都加5,纵坐标不变呢?
探究新知
7.2 坐标方法的简单应用/
解: A1(-2,3),B1(-3,1),C1(-5,2),即三角形
ABC向左平移了6个单位长度,因此所得三角形A1B1C1与三角
形ABC的大小、形状完全相同.
用类比的思想,把三角形ABC
三个顶点的横坐标都加5,纵
坐标不变,即三角形ABC向右
平移了5个单位长度,因此所
得三角形与三角形ABC的大小、
形状完全相同.
探究新知
7.2 坐标方法的简单应用/
问题2:如图,将三角形ABC三个顶点的纵坐标都减去5,横坐
标不变,猜想:三角形A2B2C2与三角形ABC的大小、形状和位置 上有什么关系?
用类比的思想,探究得
到三角形A2B2C2与三角形ABC
的大小、形状完全相同,可以
看作将三角形ABC向下平移5
个单位长度.
探究新知
7.2 坐标方法的简单应用/
问题3:如图,将三角形ABC三个顶点的横坐标都减去
同时纵坐标减去5,又能得到什么结论?
将三角形ABC三个顶点的
横坐标都减去 6,同时纵坐标
减去5,分别得到点的坐标是
(-2,-2),( -5,-3 ),
(-3,-4 ),依次连接这三点,
可以发现所得三角形可以由三
角形ABC先向左平移6个单位
长度,再向下平移5个单位长
度得到.三角形的大小、形状
6,
完全相同.
探究新知
7.2 坐标方法的简单应用/
问题4:如图所示,正方形ABCD四个顶点的坐标分别是A(-2,
4),B(-2,3),C(-1,3),D(-1,4),将正方形ABCD 向下平移7个单位长度,再向右平移8个单位长度,两次平移后 四个顶点相应变为点E,F,G,H.
(1)点E,F,G,H的坐标分别是什么?
探究新知
7.2 坐标方法的简单应用/
问题4:如图所示,正方形ABCD四个顶点的坐标分别是A(-2,
4),B(-2,3),C(-1,3),D(-1,4),将正方形
ABCD向下平移7个单位长度,再向右平移8个单位长度,两次 平移后四个顶点相应变为点E,F,G,H.
(2)如果直接平移正方形ABCD,使点A移到点E,它和我们
前面得到的正方形位置相同吗?
探究新知
7.2 坐标方法的简单应用/
点E,F,G,H的坐标分别是:(6,-3),(6,-4),
(7,-4),(7,-3).若直接平移正方形ABCD,使点A
移到点E,它就和我们前面得到的正方形位置相同.
探究新知
7.2 坐标方法的简单应用/
问题5:通过前面问题的探究,你能总结图形上点的坐标的某
种变化引起了图形怎样的平移吗?
在平面直角坐标系内,如果把一个图形各个点的横坐标
都加(或减去)一个正数a,相应的新图形就是把原图形向右
(或向左)平移a个单位长度;如果把它各个点的纵坐标都加
(或减去)一个正数b,相应的新图形就是把原图形向上(或 向下)平移b个单位长度.
探究新知
7.2 坐标方法的简单应用/
1
2
归纳总结
(1)原图形向右(左)平移a个单位长度:(a>0)
原图形上的点P(x,y) 向右平移a个单位 P (x+a,y)
原图形上的点P (x,y) 向左平移a个单位 P (x-a,y)
(2)原图形向上(下)平移b个单位长度:(b>0)
原图形上的点P(x,y) 向上平移b个单位 P3(x,y+b)
原图形上的点P(x,y) 向下平移b个单位 P4(x,y-b)
探究新知
7.2 坐标方法的简单应用/
平面直角坐标系内图形的平移
素养考点
1
例2 如图,在平面直角坐标系中,P(a,b)是三角形ABC的边AC上
一点,三角形ABC经平移后点P的对应点为P1(a+6,b+2).
y
(1)请画出上述平移后的三角
形A1B1C1,并写出点A、C、
A1、C1的坐标;
A1
P1
1
P
1
B
1
解:(1)三角形A1B1C1如图所示,
各点的坐标分别为A(-3,2)、
C
x
C(-2,0)、A1(3,4)、C1(4,2);
A
B
C
1
C
O
探究新知
7.2 坐标方法的简单应用/
(2)
求出以A、C、A1、C1为顶点的四边形的面积.
y
A1
解:(2)连接AA1,CC1,
A
B1
S四边形ACC A
1 1
=
SΔAA C + SΔAC C
1 1 1
P
B
1
1
?? ? 2 ? 7 ? 7 ? S ΔAC C
S ΔAA C
1
x
2
=
O
1 1
1
∴S四边形ACC A
1 1
SΔAA C
1 1
+ SΔAC C =14.
1
P
1
C
1
C
探究新知
7.2 坐标方法的简单应用/
一个图形依次沿x轴方向、y轴方向平移后所得图形与原来
的图形相比,位置有什么变化?它们对应点的坐标之间有怎样
的关系?
平移方向和平移距离
对应点的坐标
向右平移a个单位长度,向上平移b个单位长度
(x+a , y+b)
向右平移a个单位长度,向下平移b个单位长度
(x+a , y-b)
向左平移a个单位长度,向上平移b个单位长度
(x-a , y+b)
向左平移a个单位长度,向下平移b个单位长度
(x-a , y-b)
巩固练习
7.2 坐标方法的简单应用/
2.如图,将平行四边形ABCD向左
平移2个单位长度,然后再向上平 移3个单位长度,可以得到平行四 边形A'B'C'D',画出平移后 的图形,并指出其各个顶点的坐标.
D′
C′
A′
B′
解:如图所示,四边形A′B′C′D′就是所要画的四边形,
A′(-3,1), B′(1,1), C′(2,4), D′(-2,4).
巩固练习
7.2 坐标方法的简单应用/
连 接 中 考
1.(2019?大连)在平面直角坐标系中,将点P(3,1)向下平移
A
2个单位长度,得到的点P′的坐标为(
)
A.(3,﹣1) B.(3,3)
C.(1,1) D.(5,1)
2.(2019?海南)如图,在平面直角坐标系中,已知点A(2,1),
点B(3,-1),平移线段AB,使点A落在点A1(-2,2)处,则
点B的对应点B1的坐标为(
)
C
A.(-1,-1)
C.(-1,0)
B.(1,0)
D.(3,0)
课堂检测
7.2 坐标方法的简单应用/
基
础
巩 固
题
1.(1)如图所示,将点A向右平移(
B )个单位长度可得到点B .
C.5个单位长度 D.6个单位长度
A.3个单位长度
B. 4个单位长度
(2)如图所示,将点A向下平移5个单位长度后,将重合于图中的
y
(
).
4
3
2
1
D
A
B
A.点C
C.点D
B.点F
D.点E
-4
-3 -2 -1 0
1
2 3 4
x
C
-1
D E
-2
G -3
F -4
课堂检测
7.2 坐标方法的简单应用/
基
础
巩
固
题
(3)如图所示,点G(-2,-2),将点G先向右平移6个单位长度,再
向上平移5个单位长度,得到G′,则G′的坐标为(
D ).
A.(6,5)
B.(4,5)
C.(6,3)
D.(4,3)
y
4
3
2
1
A
B
-3 -2 -1 0
-4
1 2 3
4
x
C
-1
D E
-2
G -3
F -4
课堂检测
7.2 坐标方法的简单应用/
基
础
巩
固
题
(4)如图所示,将点A先向右平移3个单位长度,再向下平移5个
单位长度,得到A′为 _( 0_,__-3_)_;将点B先向下平移5个单位长
度,再向右平移3个单位长度,得到B′为(__4_,
相距 _4_个单位长度.
-_3_)_,则A′与B′
y
4
3
2
1
A
B
-4
-3 -2 -1 0
1 2 3 4
x
C
-1
D E
-2
G -3
F -4
课堂检测
7.2 坐标方法的简单应用/
基
础
巩
固
题
2.把一个图形上的各点的横坐标都减去1,再把它的各点的纵坐
标都加上2,则这个图形的平移方式是__先__向__左__平
__再 向 上 平 移 2_个__单__位_ .
移
1_个__单__位__,__
3.点P(a,b)向左平移1个单位长度,再向上平移1个单位长
度,得到点(3,-4),则a=__4__,b= _-_5
.
课堂检测
7.2 坐标方法的简单应用/
能
力
提
升
题
1.已知线段
MN=4,MN∥y轴,若点M坐标为(-1,2),则N点
坐标为(__-1_, -_2_) 或 ( -_1_,__6_) ;
2.已知线段 MN=4,MN∥x轴,若点M坐标为(-1,2),则N点坐
标为 ( 3_,__2_) 或 ( -5_, 2_)_.
B
-
1
-
1
2
1
3
-
-
2
4
5
4
3
2
-
-
-
-
C
2
1
4
3
课堂检测
7.2 坐标方法的简单应用/
y
拓
广
探
索
题
A1
如图,三角形ABC上任
意一点P(x0,y0)经平移后得
B1
,2)
x
+2,y
+4)
C (3,0
O
x
到的对应点为P1(x0+2,y0+4),
)
)B
将三角形ABC作同样的平
移得到三角形A1B1C1.求A1、
B1、C1的坐标.
解:A(-3,2)经平移后得到(-3+2,2+4),即A1(-1,6);B(-2,-1)
经平移后得到(-2+2,-1+4),即B1(0,3);C(3,0)经平移后得到
(3+2,0+4),即C1(5,4).
C1
(
-3
A
P
1(
0
0
)
(
-2,
-13
P
(x
0,
y0
课堂小结
7.2 坐标方法的简单应用/
向下平移,纵坐标减去一个正数
沿y轴平移
向上平移,纵坐标加上一个正数
横坐标不变
图形在坐标
系中的平移
向左平移,横坐标减去一个正数
沿x轴平移
向右平移,横坐标加上一个正数
纵坐标不变
