人教版七年级下册数学课件:5.2.2平行线的判定课件(共53张PPT)
文档属性
| 名称 | 人教版七年级下册数学课件:5.2.2平行线的判定课件(共53张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-06 00:00:00 | ||
图片预览






文档简介
(共53张PPT)
5.2 平行线及其判定/
人教版
数学
七年级 下册
5.2
平行线及其判定
5.2.2
平行线的判定
第一课时
第二课时
第一课时
5.2 平行线及其判定/
利用同位角、内错角、同旁内角
判定平行线
A
l2
1
l1
2
B
返回
导入新知
5.2 平行线及其判定/
2中的直线平行吗?你是怎么判断的?
相交
图1,
在同一平面内
平行
同一平面内,不相交
的两直线叫做平行线.
图2
图 1
导入新知
5.2 平行线及其判定/
判定两条直线平行的方法有两种:
定义:在同一平面内,不相交的两条直线叫平行线.
平行公理的推论(平行线的传递性):
如果两条直线平行于同一条直线,那么两条直线平行.
同学们想一想:
除应用以上两种方法以外,是否还有其它方法呢?
素养目标
5.2 平行线及其判定/
1. 通过用直尺和三角尺画平行线的方法理解平
行线的判定方法1.
2. 能用平行线的判定方法1来推理判定方法2和 判定方法3.
3. 能够根据平行线的判定方法进行简单的推理.
探究新知
5.2 平行线及其判定/
知识点 1
同位角相等两直线平行
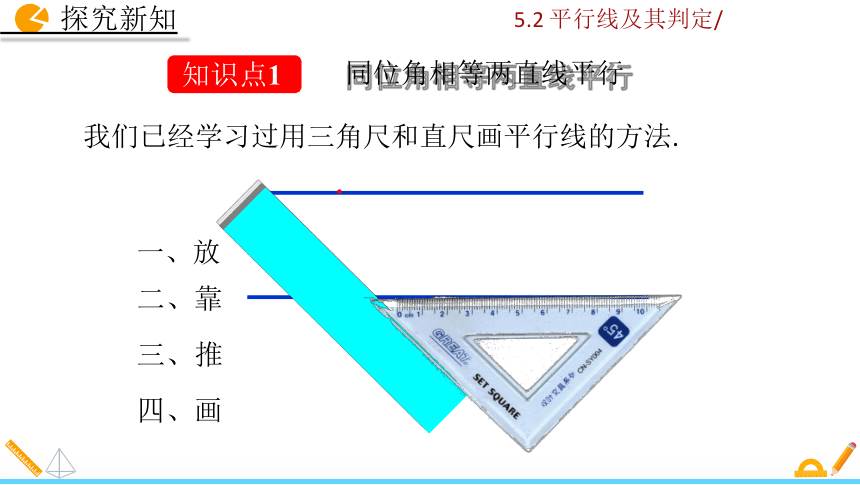
我们已经学习过用三角尺和直尺画平行线的方法.
●
一、放
二、靠
三、推
四、画
探究新知
5.2 平行线及其判定/
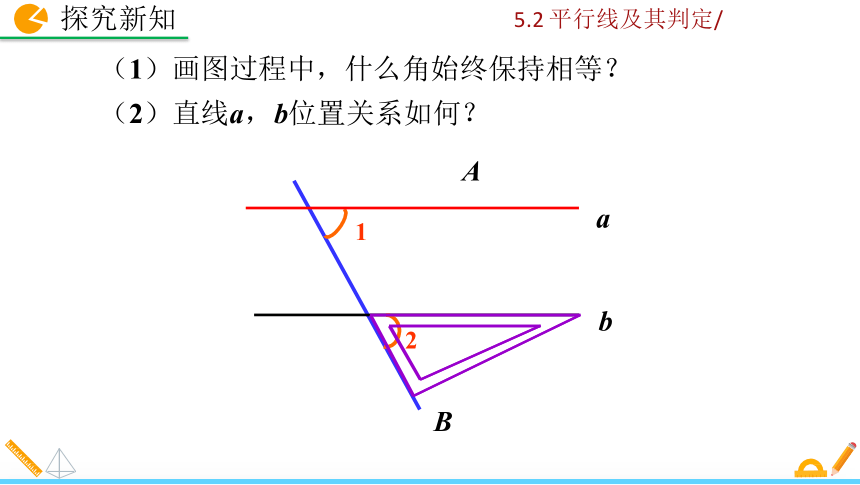
(1)画图过程中,什么角始终保持相等?
(2)直线a,b位置关系如何?
A
a
1
b
2
B
探究新知
5.2 平行线及其判定/
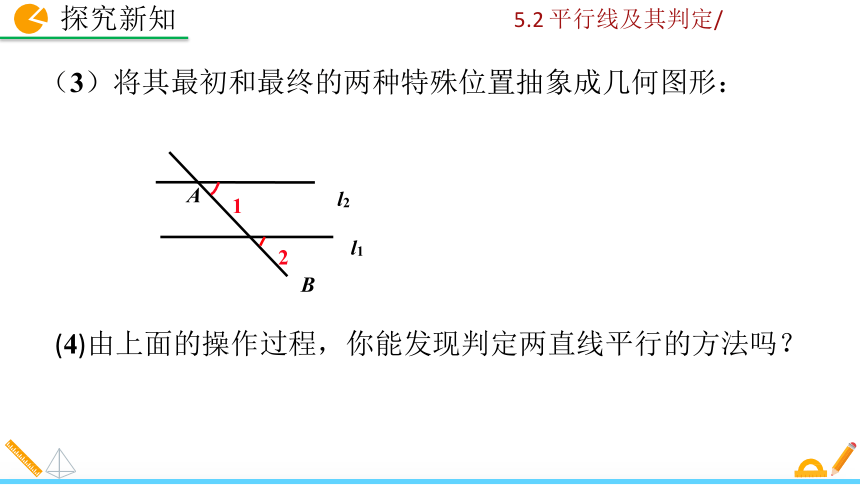
(3)将其最初和最终的两种特殊位置抽象成几何图形:
A
l2
1
l1
2
B
(4) 由上面的操作过程,你能发现判定两直线平行的方法吗?
探究新知
5.2 平行线及其判定/
判定方法1:
简单说成:同位角相等,两直线平行.
几何语言:
A
1
l2
∵∠1=∠2
∴l1∥l2
l1
2
B
两条直线被第三条直线所截,如果同位角相等,那么这两
条直线平行.
探究新知
5.2 平行线及其判定/
利用同位角相等判定两直线平行
素养考点
1
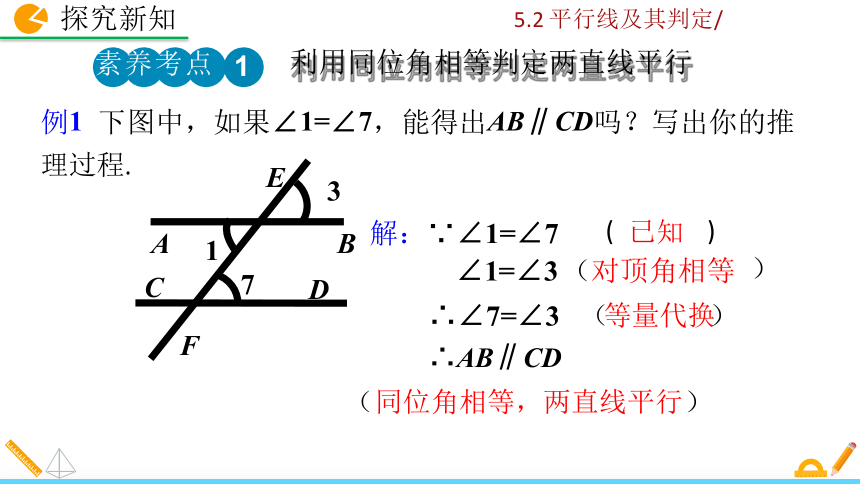
例1 下图中,如果∠1=∠7,能得出AB∥CD吗?写出你的推
理过程.
E
3
解:∵∠1=∠7
(
)
已知
A
C
B
1
∠1=∠3 ( 对顶角相等
)
7
D
∴ ∠7=∠3
∴ AB∥CD
(等量代换)
F
(同位角相等,两直线平行)
巩固练习
5.2 平行线及其判定/
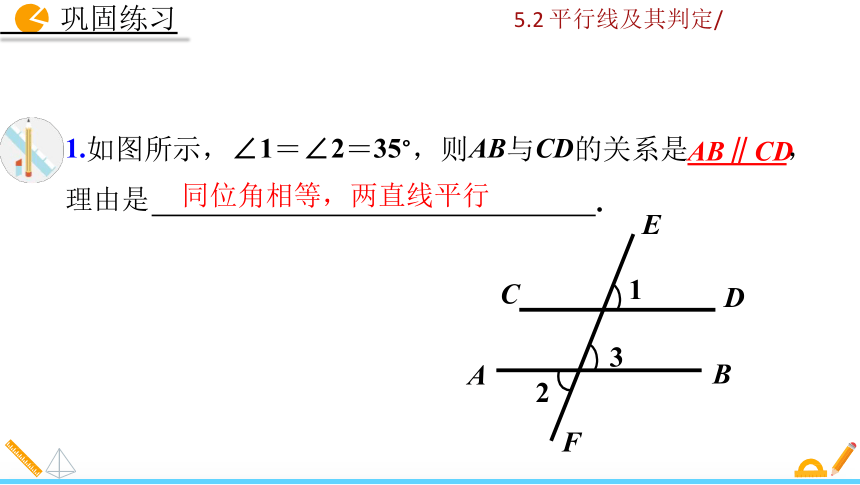
1.如图所示,∠1=∠2=35°,则AB与CD的关系是AB∥CD,
同位角相等,两直线平行
理由是
.
E
1
C
D
3
B
A
2
F
探究新知
5.2 平行线及其判定/
知识点 2
内错角相等两直线平行
两条直线被第三条直线所截,同时得到同位角、内错角和
同旁内角.由同位角相等可以判定两直线平行,那么,能否利用 内错角来判定两直线平行呢? 如图,由?3=?2,可推出a//b吗?如何推出?
1
解: ∵ ?2=?3(已知),
?3=?1(对顶角相等),
∴?1=?2.
a
3
2
b
∴ a//b(同位角相等,两直线平行).
探究新知
5.2 平行线及其判定/
判定方法2:
简单说成:内错角相等,两直线平行.
1
几何语言:
∵∠3=∠2(已知)
∴a∥b
a
3
2
b
两条直线被第三条直线所截 ,如果内错角相等,那么这两条
直线平行.
探究新知
5.2 平行线及其判定/
素养考点
1
利用内错角相等判定两直线平行
例2 完成下面证明:如图所示,CB平分∠ACD,∠1=∠3.
求证:AB∥CD.
证明:∵CB平分∠ACD,
∴∠1=∠2( 角平分线的定义_______).
∵∠1=∠3,
∴∠2=∠ 3 .
内错角相等,两直线平行_).
∴AB∥CD(
巩固练习
5.2 平行线及其判定/
2.已知∠3=45 °,∠1与∠2互余,试说明AB//CD
解:∵∠1=∠2(对顶角相等)
?
A
C
∠1与∠2互余,
∴ ∠1+∠2=90°(已知).
∴∠1=∠2=45°.
∵ ∠3=45°(已知),
∴∠ 2=∠3.
3
1
2
D
B
AB∥CD(内错角相等,两直线平行).
∴
探究新知
5.2 平行线及其判定/
知识点
利用同旁内角互补判定两直线平行
3
如图,如果?1+?2=180°
解:能,
∵?1+?2=180°(已知)
?1+?3=180°(邻补角的性质)
∴?2=?3(同角的补角相等)
∴a//b(同位角相等,两直线平行)
,你能判定a//b吗?
c
3
a
1
2
b
探究新知
5.2 平行线及其判定/
判定方法3:
简单说成:同旁内角互补,两直线平行.
几何语言:
∵∠1+∠2=180°(已知)
3
a
1
2
b
∴a∥b(同旁内角互补,两直线平行)
两条直线被第三条直线所截 ,如果同旁内角互补,那么这两
条直线平行.
探究新知
5.2 平行线及其判定/
素养考点
1
利用同旁内角互补判定两直线平行
例3 如图:直线AB、CD都和AE相交,且
∠1+∠A=180?.求证:AB//CD
B
A
2
C
D
3
1
E
已知
证明:∵∠1+∠A=180?
(
)
∠1=∠2
(对顶角相等 )
∴∠2+∠A=180?
等量代换
(
)
∴
AB∥CD
(
)
同旁内角互补,两直线平行
巩固练习
5.2 平行线及其判定/
3.根据条件完成填空.
E
①
∵
∴
∵
∴
∠2 = ∠ 6(已知)
A B_∥C D_(同位角相等,两直线平行)
2
1
B
A
4
3
②
∠3 = ∠5(已知)
_A_B_∥C D_(内错角相等,两直线平行 )
5
6
D
C
8
7
∠4 +∠ 5_=180o(已知)
③∵
∴
F
B∥C D_(
_A
)
同旁内角互补,两直线平行
巩固练习
5.2 平行线及其判定/
连 接 中 考
(2019?南京)结合图,用符号语言表达定理“同旁内角互补,
∠
1_+ ∠ 3_= 1_8_0_°
两直线平行”的推理形式:∵
∴a∥b.
,
c
2
a
4
3
1
b
课堂检测
5.2 平行线及其判定/
题
基
础
巩
固
1.如图,可以确定AB∥CE的条件是(
)
C
A.∠2=∠B
A
E
B. ∠1=∠A
2
3
C. ∠3=∠B
1
B
C
D
D. ∠3=∠A
课堂检测
5.2 平行线及其判定/
题
基
础
巩
固
2.如图,已知∠1=30°,∠2或∠3满足条件_∠__2_=
则a//b.
1_5_0_°或_
∠3=30°_
c
a
3
2
1
b
课堂检测
5.2 平行线及其判定/
固 题
基
础
巩
AB
∥
CD,
3.如图.(1)从∠1=∠4,可以推出
理由是 内 错 角 相 等 , 两 直 线 平 行 .
(2)从∠ABC +∠ BCD=180°,可以推出AB∥CD
,
同旁内角互补,两直线平行
理由是
.
A
D
3
4
1
5
2
B
C
课堂检测
5.2 平行线及其判定/
题
基
础
巩
固
,可以推出AD∥BC,理由是
(3)从∠
=∠
3
2
___内__错__角__相__等__,__两__直__线
平行
.
ABC
,可以推出AB∥CD,
(4)从∠5=∠
理由是
__ 同 位 角 相 等,两直线平行
.
A
D
3
4
1
5
2
B
C
课堂检测
5.2 平行线及其判定/
基
础 巩
固
题
F
E
C
4.根据条件完成填空.
1
3
①
∵ ∠1 = ∠ 2_(已知)
AB∥CE( 内错角相等,两直线平行
∴
∵
)
5
+_∠ 3 =180o(已知)
②
∠1
2
4
A
)
B
D
∴CD∥BF(
同旁内角互补,两直线平行
∵ ∠1 +∠5 =180o(已知)
③
∴
A__B_∥_C E (同旁内角互补,两直线平行
)
∵ ∠4 +_∠ 3 =180o(已知)
④
∴ CE∥AB( 同旁内角互补,两直线平行 )
课堂检测
5.2 平行线及其判定/
题
能
力
提
升
如图,已知∠1= ∠3,AC平分∠DAB,你能判断哪两条直
线平行?请说明理由?
C
D
AB∥CD.
解:
3
理由如下:
∵
∴
又∵
∴
AC平分∠DAB(已知),
∠1=∠2(角平分线定义).
∠1= ∠3(已知) ,
∠2=∠3(等量代换).
1
2
B
A
∴ AB∥CD(内错角相等,两直线平行).
课堂检测
5.2 平行线及其判定/
题
拓
∠
广
A,
探
∠
索
如图,已知∠MCA=
为什么?
∠
B,那么DE∥MN吗?
DEC=
DE∥MN.
∠MCA= ∠
解:
∵
∴ 又
∴
∴
M
C
D
A
A(已知)
AB∥MN(内错角相等,两直线平行.)
∵∠ DEC= ∠ B(已知)
AB∥DE(同位角相等,两直线平行.)
E
B
N
DE∥MN(如果两条直线都和第三条直线平行,那
么这两条直线也互相平行.)
课堂小结
5.2 平行线及其判定/
判定
位置关系
数量关系
线平行
两直
同位角相等
内错角相等
同旁内角互补
平行线的判定示意图
第二课时
5.2 平行线及其判定/
平行线判定方法的灵活应用
F
A
E
B
D
C
返回
导入新知
5.2 平行线及其判定/
在铺设铁轨时,两条直轨必须是互相平行的,如图:已
经知道,∠2是直角,那么再度量图中哪个角,就可以判定 两条直轨是否平行,为什么?
铁
轨
枕木
2
素养目标
5.2 平行线及其判定/
1. 进一步掌握平行线的判定方法,并会运用平
行线的判定解决问题.
2. 掌握垂直于同一条直线的两条直线互相平行.
3. 经历例题的分析过程,从中体会转化的思想和 分析问题的方法,进一步培养推理能力.
探究新知
5.2 平行线及其判定/
知识点
平行线判定方法的灵活应用
1
例1 如图,直线EF与∠ABC的一边BA相交于D,
∠B+∠ADE=180°,EF与BC平行吗?
为什么?
A
1
E
F
解:
EF//BC.理由如下:
D
∵
∠B+ ∠1=180°(已知 ),
∠1= ∠2(对顶角相等 ),
∠B+ ∠2=180°(等量代换 ).
2
B
C
∴
∴
EF∥BC( 同旁内角互补,两直线平行
).
巩固练习
5.2 平行线及其判定/
1.如图所示,直线a,b都与直线c相交,给出的下列条件:
①∠1=∠7;②∠3=∠5;③∠1+∠8=180°;④∠3=∠6.
其中能判断a∥b的是(
A. ①③
B. ②③
C. ③④
D. ①②③
)
D
c
1
4
a
3
2
5
8
b
7
6
探究新知
5.2 平行线及其判定/
例2 已知:如图,ABC、CDE都是直线,
求证:AC∥FD.
且∠1=∠2,∠1=∠C,
A
1
B
F
证明: ∵ ∠1
= ∠2,
2
∠1 = ∠C
(已知),
E
C
D
∴ ∠2=∠C (等量代换).
AC∥FD (同位角相等,两直线平行).
∴
巩固练习
5.2 平行线及其判定/
C
2.如图,∠1=∠2,则下列结论正确的是(
A
)
D
A. AD//BC
B. AB//CD
1
E
F
2
C. AD//EF
D. EF//BC
C
B
探究新知
5.2 平行线及其判定/
例3 已知:如图,四边形ABCD中,AC平分∠BAD,∠1=∠2,
AB与CD平行吗?为什么?
C
AB∥CD .理由如下:
答:
D
2
∵
AC平分∠BAD,∴ ∠1=∠3
.
1
3
∵∠1=∠2,
∴ ∠2=∠3 .
A
B
∵ ∠2和∠3是内错角,
AB∥CD(内错角相等,两直线平行).
∴
巩固练习
5.2 平行线及其判定/
3.如图,∠1=∠2,能判断AB∥DF吗?为什么?
解:不能.
若不能判断AB∥DF,你认为还需要再添加的一个条件是什 么呢?写出这个条件,并说明你的理由.
B
A
C
1
答:添加∠CBD=∠EDB
内错角相等,两直线平行.
E
2
F
D
探究新知
5.2 平行线及其判定/
知识点 2
在同一平面内,垂直于同一直线的两直线平行
在同一平面内,两条直线垂直于同一条直线,这两条
直线平行吗?为什么?
b
c
b⊥a,c⊥a ? b∥c
a
?
猜想:垂直于同一条直线的两条直线平行.
探究新知
5.2 平行线及其判定/
在同一平面内,b⊥a,c⊥a,试说明:b∥c.
解法1:如图,
∵b⊥a ,c ⊥a (已知),
∴∠1= ∠2 = 90°
(垂直的定义).
∴b∥c
c
b
a
(同位角相等,两直线平行).
1
2
探究新知
5.2 平行线及其判定/
在同一平面内,b⊥a,c⊥a,试说明:b∥c.
解法2:如图,
c
b
∵
b⊥a,c⊥a(已知),
a
∴∠1=∠2=90°(垂直定义).
∴b∥c(内错角相等,两直线平行).
1
2
探究新知
5.2 平行线及其判定/
在同一平面内,b⊥a,c⊥a,试说明:b∥c.
解法3:如图,
c
b
∵
b⊥a,c⊥a(已知),
∴∠1=∠2=90°(垂直定义).
a
∴
∠1+∠2=180°.
∴b∥c(同旁内角互补,两直线平行).
1 2
探究新知
5.2 平行线及其判定/
c
几何语言:
∵ b⊥a,c⊥a(已知)
a
∴b∥c(同一平面内,垂直于同一条直
的两条直线平行.)
b
1
2
线
同一平面内,垂直于同一条直线的两条直线平行.
探究新知
5.2 平行线及其判定/
平行线判定方法的灵活应用
素养考点
1
例4
如图,为了说明示意图中的平安大街与长安街是互相平行的,
在地图上量得∠1=90°,你能通过度量图中已标出的其他的角来
验证这个结论吗?说出你的理由.
解:方法1:测出∠3=90°,理由是同位角相等,
两直线平行.
方法2:测出∠2=90°,理由是同旁内角互补,两
直线平行.
方法3:测出∠5=90°,理由是内错角相等,两直线平行.
方法4:测出∠2,∠3,∠4,∠5中任意一个角为90°,
理由是同一平面内,垂直于同一直线的两直线平行.
巩固练习
5.2 平行线及其判定/
4.如图所示,木工师傅在一块木板上画两条平行线,方法是:
用角尺画木板边缘的两条垂线,这样画的理由有下列4种说法:
其中正确的是(
C )
①同位角相等,两直线平行;②内错角相等,两直线平行;
③同旁内角互补,两直线平行;④平面内垂直于同一直线的 两条直线平行.
A. ①②③
C. ①③④
①②④
B.
D.①③
巩固练习
5.2 平行线及其判定/
连 接 中 考
(2019?河池)如图,∠1=120°,要使a∥b,则∠2的大小
是(
D
)
l
2
A.60°
C.100°
B.80°
D.120°
b
1
a
课堂检测
5.2 平行线及其判定/
基
础
巩
固
题
如图所示,在下列条件中:①∠1=∠2;②∠BAD=
1.
×
∠BCD;③∠ABC=∠ADC且∠3=∠4;④∠BAD+∠ABC
×
√
=180°,能判定AB∥CD的有
×
(
)
C
A. 3个
C. 1个
B. 2个
D. 0个
课堂检测
5.2 平行线及其判定/
基
础
巩
固
题
如图所示,下列条件:①∠1=∠2;②∠A=∠4;③∠1=
2.
√
√
∠4;④∠A+∠3=180°;⑤∠C=∠BDE,其中能判定
×
AB∥DF的有(
A. 2个
C. 4个
√
×
B
B.
D.
)
3个
5个
课堂检测
5.2 平行线及其判定/
基
础
巩
固
题
如图所示,已知∠A=60°,下列条件能判定AB∥CD的是
3.
( A. B. C. D.
)
D
∠C=60°
∠E=60°
∠AFD=60°
∠AFC=60°
课堂检测
5.2 平行线及其判定/
基
础
巩
固
题
4.如图, ∠B=∠C,
∠B+∠D=180°,
E
B
A
那么BC平行DE吗?为什么?
答:BC∥DE
理由如下:
C
D
∠B=∠C ( 已知),
∵
∠B+
∠D=180°(已知),
∴ ∠C+ ∠D=180°(等量代换).
∴BC∥DE(同旁内角互补,两直线平行
).
课堂检测
5.2 平行线及其判定/
基
础
巩
固
题
A
5.已知:如图,∠1=∠C,∠2=∠B,
求证:MN∥EF.
M
N
1
2
E
F
C
证明:∵
∴
∵
∴
∴
∠1=∠C
MN∥BC
(已知),
B
(内错角相等,两直线平行).
∠2=∠B (已知),
EF∥BC
(同位角相等,两直线平行).
MN∥EF (平行于同一直线的两条直线平行 ).
0°.
课堂检测
5.2 平行线及其判定/
题
能
力
提
升
如图所示,已知BE、EC分别平分∠ABC,∠BCD,且∠1
与∠2互余,试说明AB∥DC.
解:∵∠1与∠2互余,∴∠1+∠2=9
∵BE,EC分别平分∠ABC,∠BCD,
∴∠ABC=2∠1,∠BCD=2∠2.
∴∠ABC+∠BCD
=2∠1+2∠2=2(∠1+∠2)
=180°.
∴AB∥DC.
课堂检测
5.2 平行线及其判定/
题
拓
广
探
索
如图,MF⊥NF于F,MF交AB于点E,NF交CD于点G,
∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由
解:
AB∥CD,
理由如下:
过点F向左作FQ,使∠MFQ=∠2=50°,
则∠NFQ=∠MFN-∠MFQ
=90°-50°=40°,
Q
∵AB∥FQ.
又∵∠1=140°,
∴∠1+∠NFQ=180°,
∴CD∥FQ,∴AB∥CD.
课堂小结
5.2 平行线及其判定/
判定两条直线是否平行的方法有:
1.平行线的定义.
2.如果两条直线都与第三条直线平行, 那么这两条直线也互相平行.
3.平行线的判定方法:
(1)同位角相等,
(2)内错角相等,
两直线平行.
两直线平行.
(3)同旁内角互补,
两直线平行.
4.如果两条直线都与第三条直线垂直,
那么这两条直线也互相平行.
5.2 平行线及其判定/
人教版
数学
七年级 下册
5.2
平行线及其判定
5.2.2
平行线的判定
第一课时
第二课时
第一课时
5.2 平行线及其判定/
利用同位角、内错角、同旁内角
判定平行线
A
l2
1
l1
2
B
返回
导入新知
5.2 平行线及其判定/
2中的直线平行吗?你是怎么判断的?
相交
图1,
在同一平面内
平行
同一平面内,不相交
的两直线叫做平行线.
图2
图 1
导入新知
5.2 平行线及其判定/
判定两条直线平行的方法有两种:
定义:在同一平面内,不相交的两条直线叫平行线.
平行公理的推论(平行线的传递性):
如果两条直线平行于同一条直线,那么两条直线平行.
同学们想一想:
除应用以上两种方法以外,是否还有其它方法呢?
素养目标
5.2 平行线及其判定/
1. 通过用直尺和三角尺画平行线的方法理解平
行线的判定方法1.
2. 能用平行线的判定方法1来推理判定方法2和 判定方法3.
3. 能够根据平行线的判定方法进行简单的推理.
探究新知
5.2 平行线及其判定/
知识点 1
同位角相等两直线平行
我们已经学习过用三角尺和直尺画平行线的方法.
●
一、放
二、靠
三、推
四、画
探究新知
5.2 平行线及其判定/
(1)画图过程中,什么角始终保持相等?
(2)直线a,b位置关系如何?
A
a
1
b
2
B
探究新知
5.2 平行线及其判定/
(3)将其最初和最终的两种特殊位置抽象成几何图形:
A
l2
1
l1
2
B
(4) 由上面的操作过程,你能发现判定两直线平行的方法吗?
探究新知
5.2 平行线及其判定/
判定方法1:
简单说成:同位角相等,两直线平行.
几何语言:
A
1
l2
∵∠1=∠2
∴l1∥l2
l1
2
B
两条直线被第三条直线所截,如果同位角相等,那么这两
条直线平行.
探究新知
5.2 平行线及其判定/
利用同位角相等判定两直线平行
素养考点
1
例1 下图中,如果∠1=∠7,能得出AB∥CD吗?写出你的推
理过程.
E
3
解:∵∠1=∠7
(
)
已知
A
C
B
1
∠1=∠3 ( 对顶角相等
)
7
D
∴ ∠7=∠3
∴ AB∥CD
(等量代换)
F
(同位角相等,两直线平行)
巩固练习
5.2 平行线及其判定/
1.如图所示,∠1=∠2=35°,则AB与CD的关系是AB∥CD,
同位角相等,两直线平行
理由是
.
E
1
C
D
3
B
A
2
F
探究新知
5.2 平行线及其判定/
知识点 2
内错角相等两直线平行
两条直线被第三条直线所截,同时得到同位角、内错角和
同旁内角.由同位角相等可以判定两直线平行,那么,能否利用 内错角来判定两直线平行呢? 如图,由?3=?2,可推出a//b吗?如何推出?
1
解: ∵ ?2=?3(已知),
?3=?1(对顶角相等),
∴?1=?2.
a
3
2
b
∴ a//b(同位角相等,两直线平行).
探究新知
5.2 平行线及其判定/
判定方法2:
简单说成:内错角相等,两直线平行.
1
几何语言:
∵∠3=∠2(已知)
∴a∥b
a
3
2
b
两条直线被第三条直线所截 ,如果内错角相等,那么这两条
直线平行.
探究新知
5.2 平行线及其判定/
素养考点
1
利用内错角相等判定两直线平行
例2 完成下面证明:如图所示,CB平分∠ACD,∠1=∠3.
求证:AB∥CD.
证明:∵CB平分∠ACD,
∴∠1=∠2( 角平分线的定义_______).
∵∠1=∠3,
∴∠2=∠ 3 .
内错角相等,两直线平行_).
∴AB∥CD(
巩固练习
5.2 平行线及其判定/
2.已知∠3=45 °,∠1与∠2互余,试说明AB//CD
解:∵∠1=∠2(对顶角相等)
?
A
C
∠1与∠2互余,
∴ ∠1+∠2=90°(已知).
∴∠1=∠2=45°.
∵ ∠3=45°(已知),
∴∠ 2=∠3.
3
1
2
D
B
AB∥CD(内错角相等,两直线平行).
∴
探究新知
5.2 平行线及其判定/
知识点
利用同旁内角互补判定两直线平行
3
如图,如果?1+?2=180°
解:能,
∵?1+?2=180°(已知)
?1+?3=180°(邻补角的性质)
∴?2=?3(同角的补角相等)
∴a//b(同位角相等,两直线平行)
,你能判定a//b吗?
c
3
a
1
2
b
探究新知
5.2 平行线及其判定/
判定方法3:
简单说成:同旁内角互补,两直线平行.
几何语言:
∵∠1+∠2=180°(已知)
3
a
1
2
b
∴a∥b(同旁内角互补,两直线平行)
两条直线被第三条直线所截 ,如果同旁内角互补,那么这两
条直线平行.
探究新知
5.2 平行线及其判定/
素养考点
1
利用同旁内角互补判定两直线平行
例3 如图:直线AB、CD都和AE相交,且
∠1+∠A=180?.求证:AB//CD
B
A
2
C
D
3
1
E
已知
证明:∵∠1+∠A=180?
(
)
∠1=∠2
(对顶角相等 )
∴∠2+∠A=180?
等量代换
(
)
∴
AB∥CD
(
)
同旁内角互补,两直线平行
巩固练习
5.2 平行线及其判定/
3.根据条件完成填空.
E
①
∵
∴
∵
∴
∠2 = ∠ 6(已知)
A B_∥C D_(同位角相等,两直线平行)
2
1
B
A
4
3
②
∠3 = ∠5(已知)
_A_B_∥C D_(内错角相等,两直线平行 )
5
6
D
C
8
7
∠4 +∠ 5_=180o(已知)
③∵
∴
F
B∥C D_(
_A
)
同旁内角互补,两直线平行
巩固练习
5.2 平行线及其判定/
连 接 中 考
(2019?南京)结合图,用符号语言表达定理“同旁内角互补,
∠
1_+ ∠ 3_= 1_8_0_°
两直线平行”的推理形式:∵
∴a∥b.
,
c
2
a
4
3
1
b
课堂检测
5.2 平行线及其判定/
题
基
础
巩
固
1.如图,可以确定AB∥CE的条件是(
)
C
A.∠2=∠B
A
E
B. ∠1=∠A
2
3
C. ∠3=∠B
1
B
C
D
D. ∠3=∠A
课堂检测
5.2 平行线及其判定/
题
基
础
巩
固
2.如图,已知∠1=30°,∠2或∠3满足条件_∠__2_=
则a//b.
1_5_0_°或_
∠3=30°_
c
a
3
2
1
b
课堂检测
5.2 平行线及其判定/
固 题
基
础
巩
AB
∥
CD,
3.如图.(1)从∠1=∠4,可以推出
理由是 内 错 角 相 等 , 两 直 线 平 行 .
(2)从∠ABC +∠ BCD=180°,可以推出AB∥CD
,
同旁内角互补,两直线平行
理由是
.
A
D
3
4
1
5
2
B
C
课堂检测
5.2 平行线及其判定/
题
基
础
巩
固
,可以推出AD∥BC,理由是
(3)从∠
=∠
3
2
___内__错__角__相__等__,__两__直__线
平行
.
ABC
,可以推出AB∥CD,
(4)从∠5=∠
理由是
__ 同 位 角 相 等,两直线平行
.
A
D
3
4
1
5
2
B
C
课堂检测
5.2 平行线及其判定/
基
础 巩
固
题
F
E
C
4.根据条件完成填空.
1
3
①
∵ ∠1 = ∠ 2_(已知)
AB∥CE( 内错角相等,两直线平行
∴
∵
)
5
+_∠ 3 =180o(已知)
②
∠1
2
4
A
)
B
D
∴CD∥BF(
同旁内角互补,两直线平行
∵ ∠1 +∠5 =180o(已知)
③
∴
A__B_∥_C E (同旁内角互补,两直线平行
)
∵ ∠4 +_∠ 3 =180o(已知)
④
∴ CE∥AB( 同旁内角互补,两直线平行 )
课堂检测
5.2 平行线及其判定/
题
能
力
提
升
如图,已知∠1= ∠3,AC平分∠DAB,你能判断哪两条直
线平行?请说明理由?
C
D
AB∥CD.
解:
3
理由如下:
∵
∴
又∵
∴
AC平分∠DAB(已知),
∠1=∠2(角平分线定义).
∠1= ∠3(已知) ,
∠2=∠3(等量代换).
1
2
B
A
∴ AB∥CD(内错角相等,两直线平行).
课堂检测
5.2 平行线及其判定/
题
拓
∠
广
A,
探
∠
索
如图,已知∠MCA=
为什么?
∠
B,那么DE∥MN吗?
DEC=
DE∥MN.
∠MCA= ∠
解:
∵
∴ 又
∴
∴
M
C
D
A
A(已知)
AB∥MN(内错角相等,两直线平行.)
∵∠ DEC= ∠ B(已知)
AB∥DE(同位角相等,两直线平行.)
E
B
N
DE∥MN(如果两条直线都和第三条直线平行,那
么这两条直线也互相平行.)
课堂小结
5.2 平行线及其判定/
判定
位置关系
数量关系
线平行
两直
同位角相等
内错角相等
同旁内角互补
平行线的判定示意图
第二课时
5.2 平行线及其判定/
平行线判定方法的灵活应用
F
A
E
B
D
C
返回
导入新知
5.2 平行线及其判定/
在铺设铁轨时,两条直轨必须是互相平行的,如图:已
经知道,∠2是直角,那么再度量图中哪个角,就可以判定 两条直轨是否平行,为什么?
铁
轨
枕木
2
素养目标
5.2 平行线及其判定/
1. 进一步掌握平行线的判定方法,并会运用平
行线的判定解决问题.
2. 掌握垂直于同一条直线的两条直线互相平行.
3. 经历例题的分析过程,从中体会转化的思想和 分析问题的方法,进一步培养推理能力.
探究新知
5.2 平行线及其判定/
知识点
平行线判定方法的灵活应用
1
例1 如图,直线EF与∠ABC的一边BA相交于D,
∠B+∠ADE=180°,EF与BC平行吗?
为什么?
A
1
E
F
解:
EF//BC.理由如下:
D
∵
∠B+ ∠1=180°(已知 ),
∠1= ∠2(对顶角相等 ),
∠B+ ∠2=180°(等量代换 ).
2
B
C
∴
∴
EF∥BC( 同旁内角互补,两直线平行
).
巩固练习
5.2 平行线及其判定/
1.如图所示,直线a,b都与直线c相交,给出的下列条件:
①∠1=∠7;②∠3=∠5;③∠1+∠8=180°;④∠3=∠6.
其中能判断a∥b的是(
A. ①③
B. ②③
C. ③④
D. ①②③
)
D
c
1
4
a
3
2
5
8
b
7
6
探究新知
5.2 平行线及其判定/
例2 已知:如图,ABC、CDE都是直线,
求证:AC∥FD.
且∠1=∠2,∠1=∠C,
A
1
B
F
证明: ∵ ∠1
= ∠2,
2
∠1 = ∠C
(已知),
E
C
D
∴ ∠2=∠C (等量代换).
AC∥FD (同位角相等,两直线平行).
∴
巩固练习
5.2 平行线及其判定/
C
2.如图,∠1=∠2,则下列结论正确的是(
A
)
D
A. AD//BC
B. AB//CD
1
E
F
2
C. AD//EF
D. EF//BC
C
B
探究新知
5.2 平行线及其判定/
例3 已知:如图,四边形ABCD中,AC平分∠BAD,∠1=∠2,
AB与CD平行吗?为什么?
C
AB∥CD .理由如下:
答:
D
2
∵
AC平分∠BAD,∴ ∠1=∠3
.
1
3
∵∠1=∠2,
∴ ∠2=∠3 .
A
B
∵ ∠2和∠3是内错角,
AB∥CD(内错角相等,两直线平行).
∴
巩固练习
5.2 平行线及其判定/
3.如图,∠1=∠2,能判断AB∥DF吗?为什么?
解:不能.
若不能判断AB∥DF,你认为还需要再添加的一个条件是什 么呢?写出这个条件,并说明你的理由.
B
A
C
1
答:添加∠CBD=∠EDB
内错角相等,两直线平行.
E
2
F
D
探究新知
5.2 平行线及其判定/
知识点 2
在同一平面内,垂直于同一直线的两直线平行
在同一平面内,两条直线垂直于同一条直线,这两条
直线平行吗?为什么?
b
c
b⊥a,c⊥a ? b∥c
a
?
猜想:垂直于同一条直线的两条直线平行.
探究新知
5.2 平行线及其判定/
在同一平面内,b⊥a,c⊥a,试说明:b∥c.
解法1:如图,
∵b⊥a ,c ⊥a (已知),
∴∠1= ∠2 = 90°
(垂直的定义).
∴b∥c
c
b
a
(同位角相等,两直线平行).
1
2
探究新知
5.2 平行线及其判定/
在同一平面内,b⊥a,c⊥a,试说明:b∥c.
解法2:如图,
c
b
∵
b⊥a,c⊥a(已知),
a
∴∠1=∠2=90°(垂直定义).
∴b∥c(内错角相等,两直线平行).
1
2
探究新知
5.2 平行线及其判定/
在同一平面内,b⊥a,c⊥a,试说明:b∥c.
解法3:如图,
c
b
∵
b⊥a,c⊥a(已知),
∴∠1=∠2=90°(垂直定义).
a
∴
∠1+∠2=180°.
∴b∥c(同旁内角互补,两直线平行).
1 2
探究新知
5.2 平行线及其判定/
c
几何语言:
∵ b⊥a,c⊥a(已知)
a
∴b∥c(同一平面内,垂直于同一条直
的两条直线平行.)
b
1
2
线
同一平面内,垂直于同一条直线的两条直线平行.
探究新知
5.2 平行线及其判定/
平行线判定方法的灵活应用
素养考点
1
例4
如图,为了说明示意图中的平安大街与长安街是互相平行的,
在地图上量得∠1=90°,你能通过度量图中已标出的其他的角来
验证这个结论吗?说出你的理由.
解:方法1:测出∠3=90°,理由是同位角相等,
两直线平行.
方法2:测出∠2=90°,理由是同旁内角互补,两
直线平行.
方法3:测出∠5=90°,理由是内错角相等,两直线平行.
方法4:测出∠2,∠3,∠4,∠5中任意一个角为90°,
理由是同一平面内,垂直于同一直线的两直线平行.
巩固练习
5.2 平行线及其判定/
4.如图所示,木工师傅在一块木板上画两条平行线,方法是:
用角尺画木板边缘的两条垂线,这样画的理由有下列4种说法:
其中正确的是(
C )
①同位角相等,两直线平行;②内错角相等,两直线平行;
③同旁内角互补,两直线平行;④平面内垂直于同一直线的 两条直线平行.
A. ①②③
C. ①③④
①②④
B.
D.①③
巩固练习
5.2 平行线及其判定/
连 接 中 考
(2019?河池)如图,∠1=120°,要使a∥b,则∠2的大小
是(
D
)
l
2
A.60°
C.100°
B.80°
D.120°
b
1
a
课堂检测
5.2 平行线及其判定/
基
础
巩
固
题
如图所示,在下列条件中:①∠1=∠2;②∠BAD=
1.
×
∠BCD;③∠ABC=∠ADC且∠3=∠4;④∠BAD+∠ABC
×
√
=180°,能判定AB∥CD的有
×
(
)
C
A. 3个
C. 1个
B. 2个
D. 0个
课堂检测
5.2 平行线及其判定/
基
础
巩
固
题
如图所示,下列条件:①∠1=∠2;②∠A=∠4;③∠1=
2.
√
√
∠4;④∠A+∠3=180°;⑤∠C=∠BDE,其中能判定
×
AB∥DF的有(
A. 2个
C. 4个
√
×
B
B.
D.
)
3个
5个
课堂检测
5.2 平行线及其判定/
基
础
巩
固
题
如图所示,已知∠A=60°,下列条件能判定AB∥CD的是
3.
( A. B. C. D.
)
D
∠C=60°
∠E=60°
∠AFD=60°
∠AFC=60°
课堂检测
5.2 平行线及其判定/
基
础
巩
固
题
4.如图, ∠B=∠C,
∠B+∠D=180°,
E
B
A
那么BC平行DE吗?为什么?
答:BC∥DE
理由如下:
C
D
∠B=∠C ( 已知),
∵
∠B+
∠D=180°(已知),
∴ ∠C+ ∠D=180°(等量代换).
∴BC∥DE(同旁内角互补,两直线平行
).
课堂检测
5.2 平行线及其判定/
基
础
巩
固
题
A
5.已知:如图,∠1=∠C,∠2=∠B,
求证:MN∥EF.
M
N
1
2
E
F
C
证明:∵
∴
∵
∴
∴
∠1=∠C
MN∥BC
(已知),
B
(内错角相等,两直线平行).
∠2=∠B (已知),
EF∥BC
(同位角相等,两直线平行).
MN∥EF (平行于同一直线的两条直线平行 ).
0°.
课堂检测
5.2 平行线及其判定/
题
能
力
提
升
如图所示,已知BE、EC分别平分∠ABC,∠BCD,且∠1
与∠2互余,试说明AB∥DC.
解:∵∠1与∠2互余,∴∠1+∠2=9
∵BE,EC分别平分∠ABC,∠BCD,
∴∠ABC=2∠1,∠BCD=2∠2.
∴∠ABC+∠BCD
=2∠1+2∠2=2(∠1+∠2)
=180°.
∴AB∥DC.
课堂检测
5.2 平行线及其判定/
题
拓
广
探
索
如图,MF⊥NF于F,MF交AB于点E,NF交CD于点G,
∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由
解:
AB∥CD,
理由如下:
过点F向左作FQ,使∠MFQ=∠2=50°,
则∠NFQ=∠MFN-∠MFQ
=90°-50°=40°,
Q
∵AB∥FQ.
又∵∠1=140°,
∴∠1+∠NFQ=180°,
∴CD∥FQ,∴AB∥CD.
课堂小结
5.2 平行线及其判定/
判定两条直线是否平行的方法有:
1.平行线的定义.
2.如果两条直线都与第三条直线平行, 那么这两条直线也互相平行.
3.平行线的判定方法:
(1)同位角相等,
(2)内错角相等,
两直线平行.
两直线平行.
(3)同旁内角互补,
两直线平行.
4.如果两条直线都与第三条直线垂直,
那么这两条直线也互相平行.
