第2课时 反比例 (教材P47页例2) 18张PPT
文档属性
| 名称 | 第2课时 反比例 (教材P47页例2) 18张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 971.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
人教版数学六年级下册 第四单元
反比例 (教材P47例2)
探究新知
基础练习
拓展练习
课堂小结
数学阅读
复习旧知
复习旧知
一. 判断下面的两种量是否成正比例,并说明理由。
1、三角形的高(h)一定,它的面积(s)和底(a)。
( ) ( )= ( ) 。 因为 ( ) 和( ) 的( )一定,所以三角形的面积 和底( )正比例。
2、圆的周长(C)和半径(r)。
( ) ( )= ( ) 。 因为 ( ) 和( ) 的( )一定,所以圆的周长和半径( )正比例。
3、圆的面积(S)和半径(r)。
( ) ( )= ( ) 。 因为 ( ) 和( ) 的比值( ),所以圆的面积 和半径( )正比例。
S
a
÷
h
S
a
比值
成
C
÷
r
2π
C
r
成
S
÷
r
S
r
会随着r的变化 而变化
比值
不成
πr
一. 判断下面的两种量是否成正比例,并说明理由。
4、小明要做12道数学题,做完的题和没做的题。
( ) ( )= ( ) 。 因为 ( ) 和( ) 的( )一定,所以( )正比例。
5、圆锥的高(h)一定,它的体积(V)和底面积(S)。
( ) ( )= ( ) 。 因为 ( ) 和( ) 的( )一定,所以圆锥的体积和底面积( )正比例。
6、圆柱的底面积(S)一定,它的体积(V)和高(h)。
( ) ( )= ( ) 。 因为 ( ) 和( ) 的( )一定,圆柱的体积和底面积( )正比例。
题的总数
-
已做的题数
未做的题数
已做的题数
未做的题数
和
不成
V
÷
S
h
V
S
比值
成
V
÷
h
S
V
h
比值
成
复习旧知
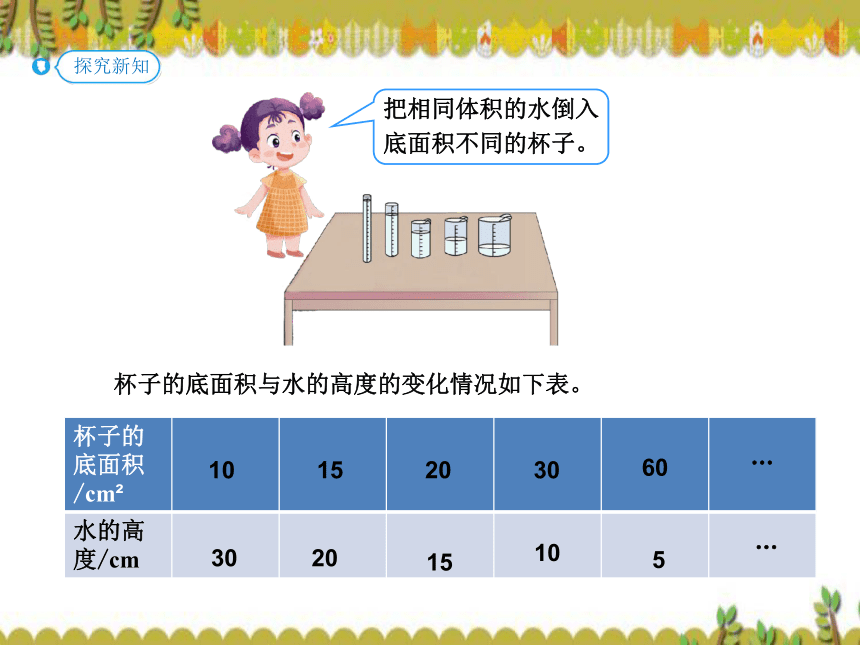
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
30
15
20
20
15
30
10
60
5
…
…
把相同体积的水倒入底面积不同的杯子。
探究新知
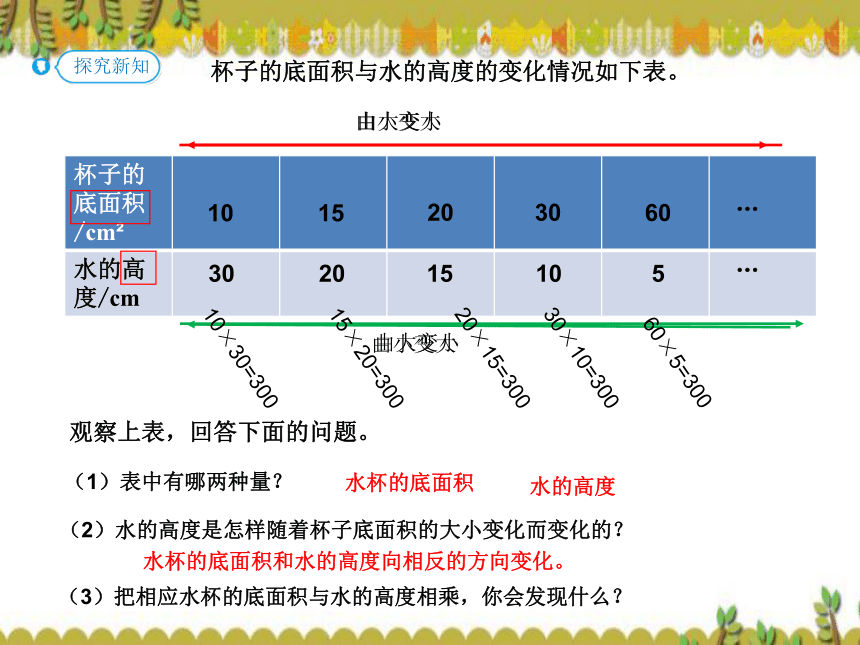
观察上表,回答下面的问题。
(3)把相应水杯的底面积与水的高度相乘,你会发现什么?
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
15
20
30
60
30
20
15
10
5
…
…
探究新知
(1)表中有哪两种量?
(2)水的高度是怎样随着杯子底面积的大小变化而变化的?
由小变大
由大变小
由大变小
由小变大
水杯的底面积
水的高度
水杯的底面积和水的高度向相反的方向变化。
10×30=300
15×20=300
20×15=300
30×10=300
60×5=300
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
15
20
30
60
30
20
15
10
5
…
…
探究新知
10×30=300
15×20=300
20×15=300
30×10=300
60×5=300
从上表可以看出,水的高度和杯子的底面积是两种相关联的量,水的高度是随着杯子的底面积的变大而不断变小的,而且水的高度与杯子的底面积的乘积总是一定的。
用式子表示它们的关系就是
底面积
高度
=
体积(不变)
×
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
15
20
30
60
30
20
15
10
5
…
…
探究新知
10×30=300
15×20=300
20×15=300
30×10=300
60×5=300
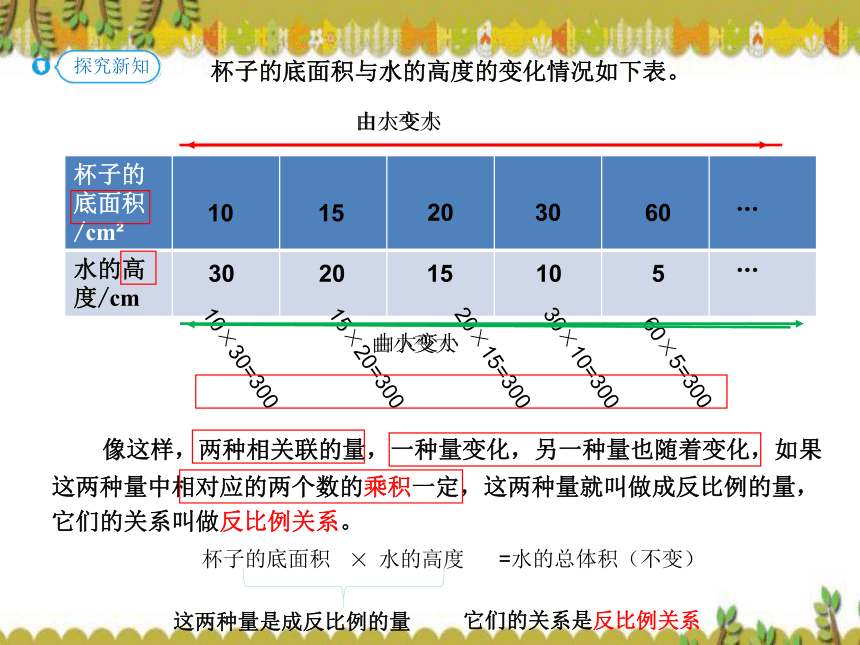
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
由小变大
由大变小
由大变小
由小变大
杯子的底面积
水的高度
×
=水的总体积(不变)
这两种量是成反比例的量
它们的关系是反比例关系
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
15
20
30
60
30
20
15
10
5
…
…
探究新知
10×30=300
15×20=300
20×15=300
30×10=300
60×5=300
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),
反比例关系可以用下面的式子表示:
x y=k
如果长方形的面积一定,长与宽成反比例关系。
如果总价一定,单价与数量成反比例关系。
基础练习
……
1、你能举出生活中反比例关系的例子吗?
每天运的吨数/吨
运货的天数/天
300
1
150
2
100
3
75
4
60
5
50
6
(1)表中有哪两种量?它们是不是相关联的量?
(2)写出几组这两种量中相对应的两个数的积,并比较积的大小,说一
说这个积表示什么。
基础练习
2、
有每天运的吨数和运货的天数两个量,这两个量是相关联的两个量。
300×1=300
150×2=300
100×3=300
75×4=300
60×5=300
50×6=300
它们的积相等,这个积表示要运走的货物总量。
每天运的吨数/吨
运货的天数/天
300
1
150
2
100
3
75
4
60
5
50
6
(3)运货的天数与每天运的吨数成反比例关系吗?为什么?
基础练习
2、
运货的天数与每天运的吨数成反比例关系。因为这两个量是相关联的量;每天运的多,需要的天数就少,每天运的少,需要的天数就多;通过上面的计算,运货的天数与每天运的吨数的乘积不变,说明要运走的货物总量是一定的。所以它们成反比例关系。
拓展练习
小明拿100元到书店买书,他可以买到什么价位的书和数量关系如下 图,请你补充完整,然后再回答下面问题。
单价/元 10 20
数量/本 50 25
10
2
5
4
1、小明买的书的数量和书的单价成反比例关系吗?为什么?
小明买的书的数量和书的单价成反比例关系,因为这两个量是两个相关联的量,一个量变化 ,另一个量也会变化,而且这两个量的乘积是一定的。
2、你能用图象表示这两个量的关系吗?
拓展练习
小明拿300元到书店买书,他可以买到什么价位的书和数量关系如下 图,请你补充完整,然后再回答下面问题。
单价/元 30 15
数量/本 15 30
10
20
20
10
数量/本
单价/元
0
5
10
15
20
25
30
35
40
45
50
10
20
30
40
50
60
70
拓展练习
你能把5本、25本、35本、40本时的单价表示出来吗。
单价/元 30 15
数量/本 15 30
10
20
20
10
数量/本
单价/元
0
5
10
15
20
25
30
35
40
45
50
10
20
30
40
50
60
70
拓展练习
把这些点连起来,你发现什么?
单价/元 30 15
数量/本 15 30
10
20
20
10
数量/本
单价/元
0
5
10
15
20
25
30
35
40
45
50
10
20
30
40
50
60
70
拓展练习
正比例图象
反比例图象
当一个量变大时,另一个量也随着变大,反之,当一个量变小时,另一个量也随着变小。图象是一条直线。
当一个量变大时,另一个量反而变小,反之,当一个量变小时,另一个量反而变大。图象是一条曲线。
我们到初中以后会对图象做进一步研究,目前大家只要记住两个图象的特征就行。
课堂小结
数学阅读
话说上次正反比例到数学王国之后,先由正比例做了自我介绍,大家都认识了正比例,和正比例的关系相处得好了些,这天大家无事,又聚在一起,问起反比例,让反比例也做一个自我介绍。
反比例看着大家都和正比例关系变好了,也很着急,今天正好是个机会,所以连忙向大家做起自我介绍来:
“知道了我哥哥——正比例,想了解我就容易多了。正比例的特点是两种相关 联的量,一种量变化,另一种量也随之变化,但是这两种量的比值(商)不变,这两种量就成正比例,它们的关系叫做正比例关系。我和哥哥不同的是,这两种量中相对应的两个数的积一定,这两种量就叫做成反比例, 它们的关系叫做反比例关系。简单来说,就是一个量变化,另一个量与之变化方向相反,这两个量的乘积始终不变。我举一个例子,大家就明白了,假如你有一杯水,要全部倒进不同粗细的圆柱杯里,当你倒到底面小的杯子里时,水一定比较高,而当你把水倒进底面大的杯子里时,水一定比较低,这种情况下,圆柱杯的底面积与装水的高度就是两个成反比例的量,它们关系就是反比例关系。在生 活中同样也有许多反比例的例子,如:当路程一定时,速度和时间成反比例;当总价一定时, 单价与数量成反比例;当工作总量一定时,工作效率和工作时间成反比例等等。我就是专门来表示上面这种关系的。 ”
听完正反比例两兄弟的自述,数学王国的公民们对他们有了全新的认识。从那以后,大家 开始慢慢接受他们,这两兄弟也快乐地生活在了数学王国里.....(完)
正反比例的故事(二)
人教版数学六年级下册 第四单元
反比例 (教材P47例2)
探究新知
基础练习
拓展练习
课堂小结
数学阅读
复习旧知
复习旧知
一. 判断下面的两种量是否成正比例,并说明理由。
1、三角形的高(h)一定,它的面积(s)和底(a)。
( ) ( )= ( ) 。 因为 ( ) 和( ) 的( )一定,所以三角形的面积 和底( )正比例。
2、圆的周长(C)和半径(r)。
( ) ( )= ( ) 。 因为 ( ) 和( ) 的( )一定,所以圆的周长和半径( )正比例。
3、圆的面积(S)和半径(r)。
( ) ( )= ( ) 。 因为 ( ) 和( ) 的比值( ),所以圆的面积 和半径( )正比例。
S
a
÷
h
S
a
比值
成
C
÷
r
2π
C
r
成
S
÷
r
S
r
会随着r的变化 而变化
比值
不成
πr
一. 判断下面的两种量是否成正比例,并说明理由。
4、小明要做12道数学题,做完的题和没做的题。
( ) ( )= ( ) 。 因为 ( ) 和( ) 的( )一定,所以( )正比例。
5、圆锥的高(h)一定,它的体积(V)和底面积(S)。
( ) ( )= ( ) 。 因为 ( ) 和( ) 的( )一定,所以圆锥的体积和底面积( )正比例。
6、圆柱的底面积(S)一定,它的体积(V)和高(h)。
( ) ( )= ( ) 。 因为 ( ) 和( ) 的( )一定,圆柱的体积和底面积( )正比例。
题的总数
-
已做的题数
未做的题数
已做的题数
未做的题数
和
不成
V
÷
S
h
V
S
比值
成
V
÷
h
S
V
h
比值
成
复习旧知
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
30
15
20
20
15
30
10
60
5
…
…
把相同体积的水倒入底面积不同的杯子。
探究新知
观察上表,回答下面的问题。
(3)把相应水杯的底面积与水的高度相乘,你会发现什么?
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
15
20
30
60
30
20
15
10
5
…
…
探究新知
(1)表中有哪两种量?
(2)水的高度是怎样随着杯子底面积的大小变化而变化的?
由小变大
由大变小
由大变小
由小变大
水杯的底面积
水的高度
水杯的底面积和水的高度向相反的方向变化。
10×30=300
15×20=300
20×15=300
30×10=300
60×5=300
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
15
20
30
60
30
20
15
10
5
…
…
探究新知
10×30=300
15×20=300
20×15=300
30×10=300
60×5=300
从上表可以看出,水的高度和杯子的底面积是两种相关联的量,水的高度是随着杯子的底面积的变大而不断变小的,而且水的高度与杯子的底面积的乘积总是一定的。
用式子表示它们的关系就是
底面积
高度
=
体积(不变)
×
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
15
20
30
60
30
20
15
10
5
…
…
探究新知
10×30=300
15×20=300
20×15=300
30×10=300
60×5=300
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
由小变大
由大变小
由大变小
由小变大
杯子的底面积
水的高度
×
=水的总体积(不变)
这两种量是成反比例的量
它们的关系是反比例关系
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
15
20
30
60
30
20
15
10
5
…
…
探究新知
10×30=300
15×20=300
20×15=300
30×10=300
60×5=300
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),
反比例关系可以用下面的式子表示:
x y=k
如果长方形的面积一定,长与宽成反比例关系。
如果总价一定,单价与数量成反比例关系。
基础练习
……
1、你能举出生活中反比例关系的例子吗?
每天运的吨数/吨
运货的天数/天
300
1
150
2
100
3
75
4
60
5
50
6
(1)表中有哪两种量?它们是不是相关联的量?
(2)写出几组这两种量中相对应的两个数的积,并比较积的大小,说一
说这个积表示什么。
基础练习
2、
有每天运的吨数和运货的天数两个量,这两个量是相关联的两个量。
300×1=300
150×2=300
100×3=300
75×4=300
60×5=300
50×6=300
它们的积相等,这个积表示要运走的货物总量。
每天运的吨数/吨
运货的天数/天
300
1
150
2
100
3
75
4
60
5
50
6
(3)运货的天数与每天运的吨数成反比例关系吗?为什么?
基础练习
2、
运货的天数与每天运的吨数成反比例关系。因为这两个量是相关联的量;每天运的多,需要的天数就少,每天运的少,需要的天数就多;通过上面的计算,运货的天数与每天运的吨数的乘积不变,说明要运走的货物总量是一定的。所以它们成反比例关系。
拓展练习
小明拿100元到书店买书,他可以买到什么价位的书和数量关系如下 图,请你补充完整,然后再回答下面问题。
单价/元 10 20
数量/本 50 25
10
2
5
4
1、小明买的书的数量和书的单价成反比例关系吗?为什么?
小明买的书的数量和书的单价成反比例关系,因为这两个量是两个相关联的量,一个量变化 ,另一个量也会变化,而且这两个量的乘积是一定的。
2、你能用图象表示这两个量的关系吗?
拓展练习
小明拿300元到书店买书,他可以买到什么价位的书和数量关系如下 图,请你补充完整,然后再回答下面问题。
单价/元 30 15
数量/本 15 30
10
20
20
10
数量/本
单价/元
0
5
10
15
20
25
30
35
40
45
50
10
20
30
40
50
60
70
拓展练习
你能把5本、25本、35本、40本时的单价表示出来吗。
单价/元 30 15
数量/本 15 30
10
20
20
10
数量/本
单价/元
0
5
10
15
20
25
30
35
40
45
50
10
20
30
40
50
60
70
拓展练习
把这些点连起来,你发现什么?
单价/元 30 15
数量/本 15 30
10
20
20
10
数量/本
单价/元
0
5
10
15
20
25
30
35
40
45
50
10
20
30
40
50
60
70
拓展练习
正比例图象
反比例图象
当一个量变大时,另一个量也随着变大,反之,当一个量变小时,另一个量也随着变小。图象是一条直线。
当一个量变大时,另一个量反而变小,反之,当一个量变小时,另一个量反而变大。图象是一条曲线。
我们到初中以后会对图象做进一步研究,目前大家只要记住两个图象的特征就行。
课堂小结
数学阅读
话说上次正反比例到数学王国之后,先由正比例做了自我介绍,大家都认识了正比例,和正比例的关系相处得好了些,这天大家无事,又聚在一起,问起反比例,让反比例也做一个自我介绍。
反比例看着大家都和正比例关系变好了,也很着急,今天正好是个机会,所以连忙向大家做起自我介绍来:
“知道了我哥哥——正比例,想了解我就容易多了。正比例的特点是两种相关 联的量,一种量变化,另一种量也随之变化,但是这两种量的比值(商)不变,这两种量就成正比例,它们的关系叫做正比例关系。我和哥哥不同的是,这两种量中相对应的两个数的积一定,这两种量就叫做成反比例, 它们的关系叫做反比例关系。简单来说,就是一个量变化,另一个量与之变化方向相反,这两个量的乘积始终不变。我举一个例子,大家就明白了,假如你有一杯水,要全部倒进不同粗细的圆柱杯里,当你倒到底面小的杯子里时,水一定比较高,而当你把水倒进底面大的杯子里时,水一定比较低,这种情况下,圆柱杯的底面积与装水的高度就是两个成反比例的量,它们关系就是反比例关系。在生 活中同样也有许多反比例的例子,如:当路程一定时,速度和时间成反比例;当总价一定时, 单价与数量成反比例;当工作总量一定时,工作效率和工作时间成反比例等等。我就是专门来表示上面这种关系的。 ”
听完正反比例两兄弟的自述,数学王国的公民们对他们有了全新的认识。从那以后,大家 开始慢慢接受他们,这两兄弟也快乐地生活在了数学王国里.....(完)
正反比例的故事(二)
