人教B版 高中数学 选修2-1 2.1.1曲线与方程的概念(共32张PPT)
文档属性
| 名称 | 人教B版 高中数学 选修2-1 2.1.1曲线与方程的概念(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 854.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-08 00:00:00 | ||
图片预览







文档简介
(共32张PPT)
2.1 曲线与方程
人教B版 选修2-1 2.1.1 曲线与方程的概念
使同学们对曲线与方程有更系统更完整的认识.
培养同学们分析曲线的能力.
教学目标
知识与能力
培养学生学会从“感性认识”到“理性认识”过程中获取新知.
通过对圆与方程的感性认识,坐标法研究曲线的方法,进一步学习曲线与方程.
过程与方法
情感态度与价值观
掌握曲线的方程,曲线的方程的概念.
使同学们理解曲线的方程的概念.
分析曲线的能力.
教学重难点
重点
难点
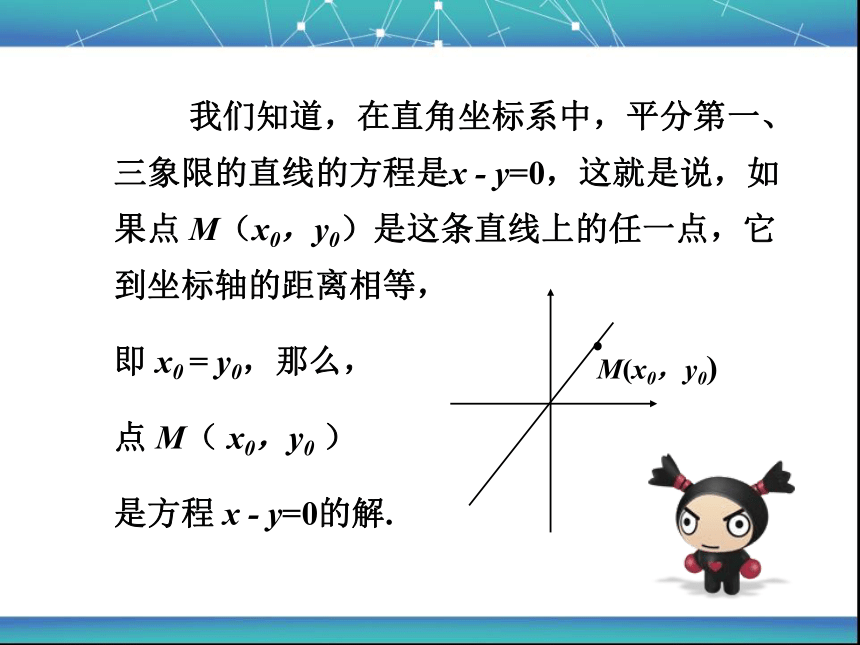
我们知道,在直角坐标系中,平分第一、三象限的直线的方程是x - y=0,这就是说,如果点 M(x0,y0)是这条直线上的任一点,它到坐标轴的距离相等,
即 x0 = y0,那么,
点 M( x0,y0 )
是方程 x - y=0的解.
M(x0,y0)
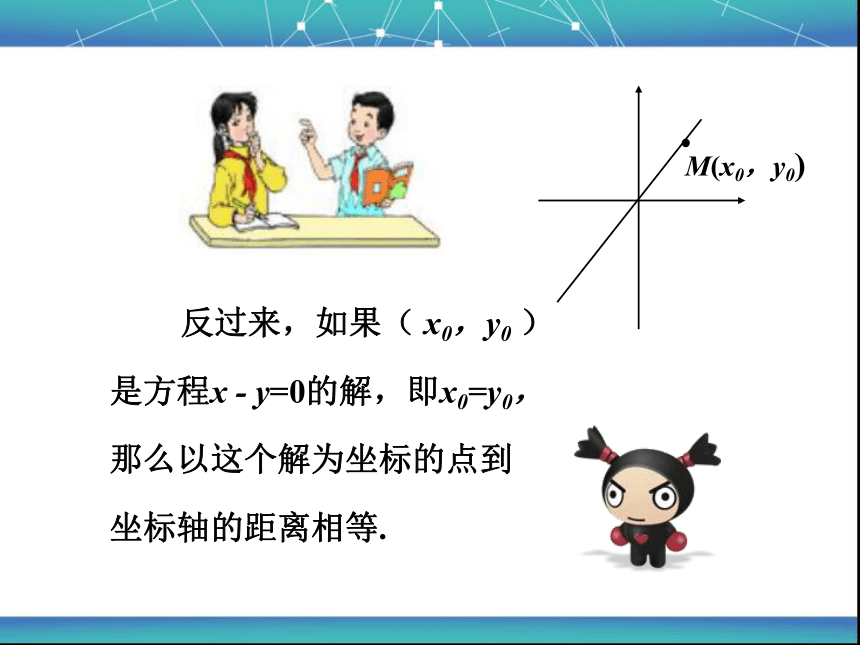
反过来,如果( x0,y0 )是方程x - y=0的解,即x0=y0, 那么以这个解为坐标的点到坐标轴的距离相等.
M(x0,y0)
一般的,在直角坐标系中,如果某曲线 C( 看作点的集合或适合某种条件的点的轨迹)上的点与一个一元二次方程 : f(x,y)=0的实数解建立如下的关系:
(1)曲线上的点的坐标都是这个方程的解;
(2)以这个方程的解为坐标的点都是曲线
上的点.
那么,这个方程叫做曲线方程;这条
曲线叫做方程的曲线.
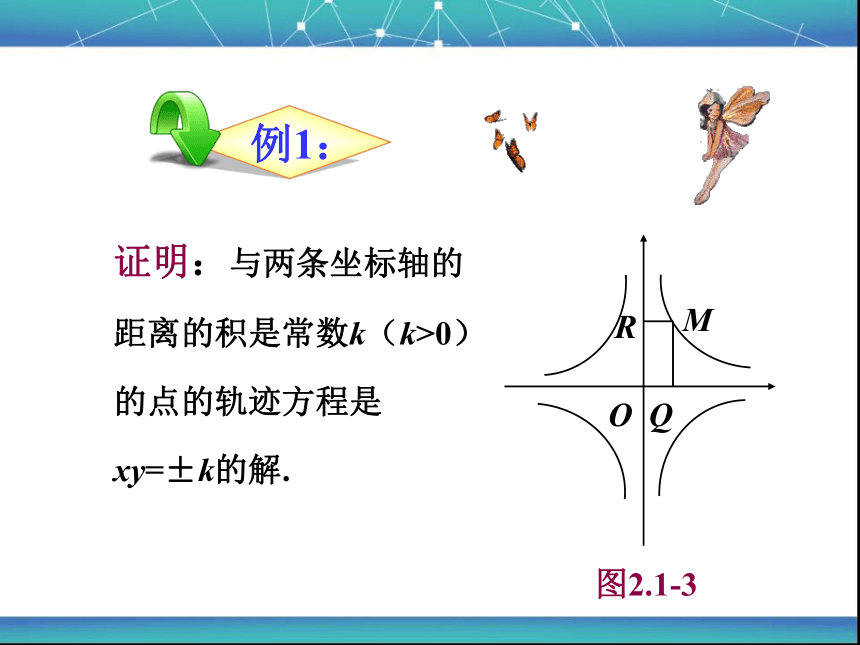
证明:与两条坐标轴的距离的积是常数k(k>0)的点的轨迹方程是xy=±k的解.
M
R
O
Q
图2.1-3
例1:
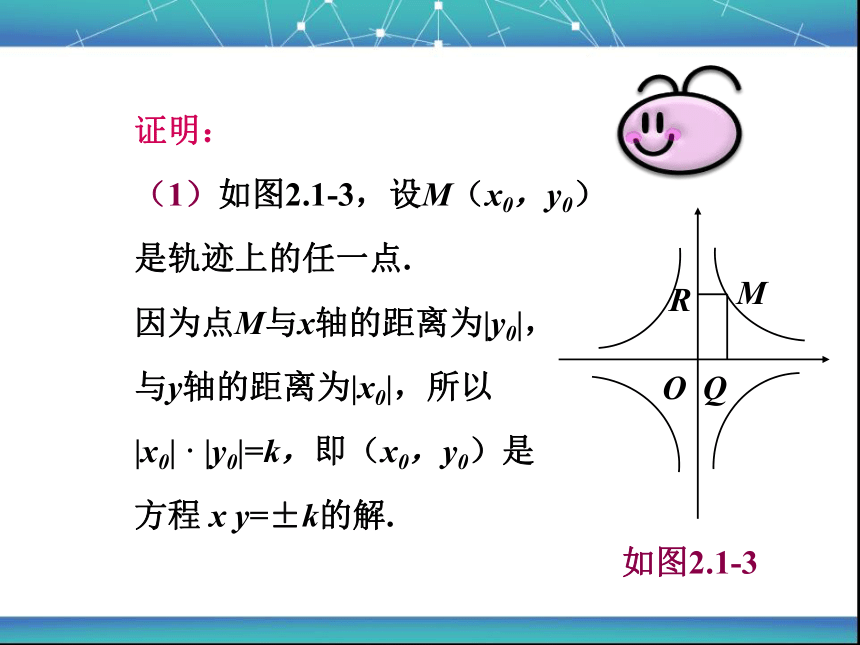
证明:
(1)如图2.1-3,设M(x0,y0)
是轨迹上的任一点.
因为点M与x轴的距离为|y0|,
与y轴的距离为|x0|,所以
|x0| · |y0|=k,即(x0,y0)是
方程 x y=±k的解.
M
R
O
Q
如图2.1-3
(2)设点M1的坐标(x1,y1)是方程xy=±k 的解则x1y1=±k 即|x1|·|y1|=k,|x1|,|y1|正是点M1到纵轴和横轴的距离,因此点M1到这两条直线的距离的积是常数k,点M1是曲线上的点.
由(1)(2)可知x y =±k是与两条坐标的距离的积为常数k(k>0)的点的轨迹方程.
已知等腰三角形三个顶点的坐标分别是A(0,3),B(-2,0),C(2,0).
问:中线AO(O为原点)所在直线的方程是 x = 0吗?为什么?
例2:
解:是,由图可知,等腰三角形ABC的边BC上的中线AO所在直线的方程是:x=0
A
B
C
O
x
y
这里的“曲线”指的是三角形ABC中BC的中线所在的直线x=0是这条曲线的方程.
在理解什么是“曲线”时,要注意曲线是满足条件的图形;在理解“方程”时,要注意方程包含对其中未知数的限制.
比如本例题中,三角形ABC中BC的中线的方程是x=0(0≥y≥3).
注意!
课堂小结
(1)曲线上的点的坐标都是这个方程的解
(2)以这个方程的解为坐标的点都是曲线
上的点
那么,这个方程叫做曲线方程;
“曲线方程”的概念 :
(1)曲线上的点的坐标都是这个方程的解
(2)以这个方程的解为坐标的点都是曲线
上的点
那么,这条曲线叫做方程的曲线.
“方程的曲线”的概念 :
课堂练习
1、已知:曲线C上的任意一点P到点F(0,1)的距离比它到直线m:y=4的距离小3.不经过坐标原点的直线与曲线l相交于两个不同点A,B,且以AB为直径的原经过坐标原点O
(1)求曲线方程C的方程;
(2)求证:直线l过顶点,并求出该顶点的坐标;
(3)三角形ABF的面积是否存在最小值?若不存在请说明理由;
(4)设曲线C在点A、B处发热切线分别为l1,l2,证明l1与l2的焦点必定在定直线m:y=-4上.
解: (1)解法1:依题意,可知,曲线C是“平面内到顶点F(0,1)的距离与到定直线y=-1的距离相等的点的轨迹”,所以它是以F(0,1)为焦点,以直线y=-1为准线的抛物线.
所以曲线C的方程式x2=4y.
(1)解法二:
设点P的坐标为(x,y),依题意指点P必定在直线m的上方,
即y >-4于是 |PF|= |y+4|- 3= y+1,所以 整理得x2=4y
所以曲线C的方程是x2=4y.
它是以F(0,1)为焦点,
以直线y=-1为准线的抛物线.
(2)直线l的斜率显然存在,又直线l不经过坐标原点,故可设直线l的方程为 y=kx+b(b≥0),并设A(x1,y1), B(x2,y2)
由 ,消去y,整理得
x2- 4kx - 4b=0①
∴ x1+x2=4k②
x1x2=-4b③
若以AB为直径的圆过坐标原点O则
∴x1x2+y1y2=0,
即 ④
将③带入④,
得
解的b=4或b=0(舍去)
所以x1x2=-16,⑤
∴直线l的方程为y=kx+4,
显然,直线l过定点M(0,4)
(3)由弦长公式得
把②⑤带入上式,得
设点F(0,1)到直线l:kx-y+4=0的距离为d,则
∴
∴当k=0时,S△AFB有最小值,是12
∴ △AFB的面积存在最小值,最小值是12.
(4)曲线C的方程可化为
则 ,
所以l1的方程为:
l2的方程为:
⑥
⑦
解⑥⑦联立方程组,得
所以l1与l2的焦点为
M(2k,-4)
它恒定在直线m:y=-4上.
2.下面各对方程中表示的曲线相同的一对是( ).
(A) y2=x与y=x
(B)y=x与 y / x=1
(C)|y|=|x|与y2=x2
(D)y=lgx2与y=2lgx
C
3. 如果命题“坐标满足方程f (x, y)=0的点都在曲线c上”是不正确的,那么下列命题正确的是( ).
A. 坐标满足方程f (x, y)=0的点都
不在曲线c上
B. 坐标满足方程f (x, y)=0的点有
些在曲线c上,有些不在曲线c上
C. 曲线c上的点不都满足方程f (x, y)=0
D. 一定有不在曲线c上的点,其坐标满足
方程f (x, y)=0
D
4、已知△ABC的面积为4,A、B两点的坐标分别是(-2,0)、(2,0),则顶点C的轨迹方程是
______________ .
y=2和 y =-2
5、 m=-2是直线
(2-m )x+my+3=0和
直线 x-my-3=0互相垂直的__________________ .
充分而不必要的条件
6、若直线 l1:x+y+a=0,l2:x+ay+1=0,
l3:ax+y+1=0能围成三角形,求a的取值范围.
解:由l1、l2相交,需要1·a-1·1≠0,得到
a ≠1,此时,解方程组
可解得 .即l1,l2的交点为(-1-a,1),由l1、l3相交,需1·1-a·a≠0,∴a≠±1,
又(-1-a,1) 不∈l3∴a·(-1-a)+1+1≠0,
得a≠1且a≠-2,
综上,a∈R且a≠±1且a≠-2,能保证三交点
(-1-a,1),(1,-1-a)、(-1-a,-1+a+a2)互不重合,所以所求a的范围为
a∈(-∞,-2)∪(-2,-1)∪(-1,1)∪(1,+∞).
解:如图,设围成四边形为OABC,因OABC有外接圆,且∠AOC=90°,故∠ABC=90°.
∴两条直线x+3y-7=0,kx – y – 2 = 0互相垂直,(- )·k=-1,即k=3.
7、已知直线x+3y-7=0,
kx-y-2=0和x轴、y轴围成
四边形有外接圆,求k.
2.1 曲线与方程
人教B版 选修2-1 2.1.1 曲线与方程的概念
使同学们对曲线与方程有更系统更完整的认识.
培养同学们分析曲线的能力.
教学目标
知识与能力
培养学生学会从“感性认识”到“理性认识”过程中获取新知.
通过对圆与方程的感性认识,坐标法研究曲线的方法,进一步学习曲线与方程.
过程与方法
情感态度与价值观
掌握曲线的方程,曲线的方程的概念.
使同学们理解曲线的方程的概念.
分析曲线的能力.
教学重难点
重点
难点
我们知道,在直角坐标系中,平分第一、三象限的直线的方程是x - y=0,这就是说,如果点 M(x0,y0)是这条直线上的任一点,它到坐标轴的距离相等,
即 x0 = y0,那么,
点 M( x0,y0 )
是方程 x - y=0的解.
M(x0,y0)
反过来,如果( x0,y0 )是方程x - y=0的解,即x0=y0, 那么以这个解为坐标的点到坐标轴的距离相等.
M(x0,y0)
一般的,在直角坐标系中,如果某曲线 C( 看作点的集合或适合某种条件的点的轨迹)上的点与一个一元二次方程 : f(x,y)=0的实数解建立如下的关系:
(1)曲线上的点的坐标都是这个方程的解;
(2)以这个方程的解为坐标的点都是曲线
上的点.
那么,这个方程叫做曲线方程;这条
曲线叫做方程的曲线.
证明:与两条坐标轴的距离的积是常数k(k>0)的点的轨迹方程是xy=±k的解.
M
R
O
Q
图2.1-3
例1:
证明:
(1)如图2.1-3,设M(x0,y0)
是轨迹上的任一点.
因为点M与x轴的距离为|y0|,
与y轴的距离为|x0|,所以
|x0| · |y0|=k,即(x0,y0)是
方程 x y=±k的解.
M
R
O
Q
如图2.1-3
(2)设点M1的坐标(x1,y1)是方程xy=±k 的解则x1y1=±k 即|x1|·|y1|=k,|x1|,|y1|正是点M1到纵轴和横轴的距离,因此点M1到这两条直线的距离的积是常数k,点M1是曲线上的点.
由(1)(2)可知x y =±k是与两条坐标的距离的积为常数k(k>0)的点的轨迹方程.
已知等腰三角形三个顶点的坐标分别是A(0,3),B(-2,0),C(2,0).
问:中线AO(O为原点)所在直线的方程是 x = 0吗?为什么?
例2:
解:是,由图可知,等腰三角形ABC的边BC上的中线AO所在直线的方程是:x=0
A
B
C
O
x
y
这里的“曲线”指的是三角形ABC中BC的中线所在的直线x=0是这条曲线的方程.
在理解什么是“曲线”时,要注意曲线是满足条件的图形;在理解“方程”时,要注意方程包含对其中未知数的限制.
比如本例题中,三角形ABC中BC的中线的方程是x=0(0≥y≥3).
注意!
课堂小结
(1)曲线上的点的坐标都是这个方程的解
(2)以这个方程的解为坐标的点都是曲线
上的点
那么,这个方程叫做曲线方程;
“曲线方程”的概念 :
(1)曲线上的点的坐标都是这个方程的解
(2)以这个方程的解为坐标的点都是曲线
上的点
那么,这条曲线叫做方程的曲线.
“方程的曲线”的概念 :
课堂练习
1、已知:曲线C上的任意一点P到点F(0,1)的距离比它到直线m:y=4的距离小3.不经过坐标原点的直线与曲线l相交于两个不同点A,B,且以AB为直径的原经过坐标原点O
(1)求曲线方程C的方程;
(2)求证:直线l过顶点,并求出该顶点的坐标;
(3)三角形ABF的面积是否存在最小值?若不存在请说明理由;
(4)设曲线C在点A、B处发热切线分别为l1,l2,证明l1与l2的焦点必定在定直线m:y=-4上.
解: (1)解法1:依题意,可知,曲线C是“平面内到顶点F(0,1)的距离与到定直线y=-1的距离相等的点的轨迹”,所以它是以F(0,1)为焦点,以直线y=-1为准线的抛物线.
所以曲线C的方程式x2=4y.
(1)解法二:
设点P的坐标为(x,y),依题意指点P必定在直线m的上方,
即y >-4于是 |PF|= |y+4|- 3= y+1,所以 整理得x2=4y
所以曲线C的方程是x2=4y.
它是以F(0,1)为焦点,
以直线y=-1为准线的抛物线.
(2)直线l的斜率显然存在,又直线l不经过坐标原点,故可设直线l的方程为 y=kx+b(b≥0),并设A(x1,y1), B(x2,y2)
由 ,消去y,整理得
x2- 4kx - 4b=0①
∴ x1+x2=4k②
x1x2=-4b③
若以AB为直径的圆过坐标原点O则
∴x1x2+y1y2=0,
即 ④
将③带入④,
得
解的b=4或b=0(舍去)
所以x1x2=-16,⑤
∴直线l的方程为y=kx+4,
显然,直线l过定点M(0,4)
(3)由弦长公式得
把②⑤带入上式,得
设点F(0,1)到直线l:kx-y+4=0的距离为d,则
∴
∴当k=0时,S△AFB有最小值,是12
∴ △AFB的面积存在最小值,最小值是12.
(4)曲线C的方程可化为
则 ,
所以l1的方程为:
l2的方程为:
⑥
⑦
解⑥⑦联立方程组,得
所以l1与l2的焦点为
M(2k,-4)
它恒定在直线m:y=-4上.
2.下面各对方程中表示的曲线相同的一对是( ).
(A) y2=x与y=x
(B)y=x与 y / x=1
(C)|y|=|x|与y2=x2
(D)y=lgx2与y=2lgx
C
3. 如果命题“坐标满足方程f (x, y)=0的点都在曲线c上”是不正确的,那么下列命题正确的是( ).
A. 坐标满足方程f (x, y)=0的点都
不在曲线c上
B. 坐标满足方程f (x, y)=0的点有
些在曲线c上,有些不在曲线c上
C. 曲线c上的点不都满足方程f (x, y)=0
D. 一定有不在曲线c上的点,其坐标满足
方程f (x, y)=0
D
4、已知△ABC的面积为4,A、B两点的坐标分别是(-2,0)、(2,0),则顶点C的轨迹方程是
______________ .
y=2和 y =-2
5、 m=-2是直线
(2-m )x+my+3=0和
直线 x-my-3=0互相垂直的__________________ .
充分而不必要的条件
6、若直线 l1:x+y+a=0,l2:x+ay+1=0,
l3:ax+y+1=0能围成三角形,求a的取值范围.
解:由l1、l2相交,需要1·a-1·1≠0,得到
a ≠1,此时,解方程组
可解得 .即l1,l2的交点为(-1-a,1),由l1、l3相交,需1·1-a·a≠0,∴a≠±1,
又(-1-a,1) 不∈l3∴a·(-1-a)+1+1≠0,
得a≠1且a≠-2,
综上,a∈R且a≠±1且a≠-2,能保证三交点
(-1-a,1),(1,-1-a)、(-1-a,-1+a+a2)互不重合,所以所求a的范围为
a∈(-∞,-2)∪(-2,-1)∪(-1,1)∪(1,+∞).
解:如图,设围成四边形为OABC,因OABC有外接圆,且∠AOC=90°,故∠ABC=90°.
∴两条直线x+3y-7=0,kx – y – 2 = 0互相垂直,(- )·k=-1,即k=3.
7、已知直线x+3y-7=0,
kx-y-2=0和x轴、y轴围成
四边形有外接圆,求k.
