人教B版 选修2-1 高中数学 2.2.1椭圆的标准方程(共44张PPT)
文档属性
| 名称 | 人教B版 选修2-1 高中数学 2.2.1椭圆的标准方程(共44张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-08 00:00:00 | ||
图片预览











文档简介
(共44张PPT)
人教B版 选修2-1 2.2.1 椭圆的标准方程
圆锥曲线与方程
教学目标
知识与能力:
理解椭圆的概念,掌握椭圆的定义、会用椭圆的定义解决实际问题;
理解椭圆标准方程的推导过程及化简无理方程的常用的方法;
了解求椭圆的动点的伴随点的轨迹方程的一般方法.
过程与方法:
注重数形结合,掌握解析法研究几何问题的一般方法;
注重探索能力的培养.
情感态度与价值观:
探究方法激发学生的求知欲,培养浓厚的学习兴趣;
进行数学美育的渗透,用哲学的观点指导学习.
教学重难点
椭圆定义的理解及标准方程的推导
重点:
难点:
标准方程的推导
从上述的探究中,我们可以知道:把细绳的两端拉开一段距离,移动笔尖的过程中,细绳的长度保持不变,即笔尖到两个定点的距离和等于常数.
椭圆:平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹.这两个定点叫做椭圆的焦点,两个焦点间的距离叫做椭圆的焦距.
y
x
M
F1
F2
O
c
c
图2.2-1
类比利用圆的对称性建立圆方程的过程,画出适当的坐标系,建立它的方程.
如图2.2-1,以经过两焦点F1,F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立直角坐标系xOy.
y
x
M
F1
F2
O
c
c
图2.2-1
设M(x,y)是椭圆上任意一点,椭圆的焦距为2c(c>0),那么焦点F1,F2的坐标分别为(-c,0)(c,0).又设M与F1,F2的距离等于2a.
由椭圆的定义,椭圆就是集合
P={M||MF1|+|MF2|=2a}.
因为|MF1|= ,|MF2|= ,
所以
化简此方程,将左边的一个根式移到右边,得:
将这个方程两边平方,得
整理得
上式两边再平方,得
a4-2a2cx+c2x2=a2x2-2a2cx+a2c2+a2y2,
整理得
(a2-c2)x2+a2y2=a2(a2-c2),
两边同除以a2(a2-c2),得
由椭圆的定义可知,2a>2c,即a>c,
所以,a2-c2>0.
①
y
x
P
F1
F2
O
图2.2-2
观察与分析
观察图2.2-2,你能从中找出表示a,c,
的线段吗?
由图可知,|PF1|=|PF2|=a,|OF1|=|OF2|=c,|PO|= , 令b=|PO|= ,那么①式就是
(a>b>0) ②
我们把方程②叫做椭圆的标准方程,椭圆上任意一点的坐标都满足此方程.它的焦点在x轴上,两个焦点分别是F1(-c,0),F2(c,0)这里的c2=a2-b2.
y
x
M
F1
F2
O
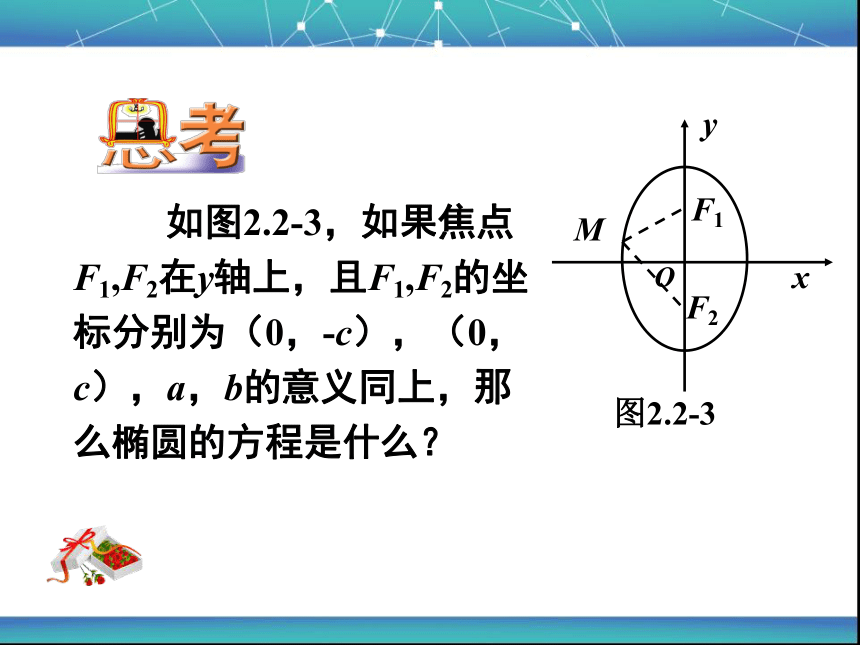
图2.2-3
如图2.2-3,如果焦点F1,F2在y轴上,且F1,F2的坐标分别为(0,-c),(0,c),a,b的意义同上,那么椭圆的方程是什么?
容易知道,此时椭圆的方程是
(a>b>0)
这个方程也是椭圆的标准方程.
例1:
已知椭圆的两个焦点坐标分别是(-2,0),(2,0),并且经过点 ,求它的标准方程.
解:因为椭圆的焦点在x轴上,所以设它的标准方程为
继续解答
(a>b>0).
由椭圆的定义知
所以
又因为c=2,所以b2=a2-c2=10-4=6.
因此,所求椭圆的标准方程为
例2:
中心在原点,一焦点为F1(0,5)的椭圆被直线y=3x-2截得的弦的中点横坐标是 ,求此椭圆的方程.
解:设椭圆的标准方程为:
(a>b>0),
则a2+b2=50…①
又设A(x1,y1),B(x2,y2),弦AB中点(x0,y0)
∵x0= ,∴y0= -2=-
继续解答
解①,②得:a2=75,b2=25,椭圆为:
×
由
…②
例3:
y
x
O
A
B
M
图 2.2-4
如图2.2-4,设点A,B的坐标分别为(-5,0),(5,0).直线AM,BM相交于点M,且它们的斜率之积是 ,求点M的轨迹方程.
分析
设点M的坐标为(x,y),那么直线AM,BM的斜率就可以用含有x,y的式子表示.由于直线AM,BM的斜率之积是 ,因此可以建立x,y之间的关系式,得出点M的轨迹方程.
解:设点M的坐标为(x,y),因为点A的坐标是(-5,0),所以,直线AM的斜率为
继续解答
(x ≠ -5);
同理,直线BM的斜率
(x ≠ 5).
由已知有
(x≠±5)
化简,得点M的轨迹方程为
( x≠±5 ).
课堂小结
1. 椭圆:
平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹.这两个定点叫做椭圆的焦点,两个焦点间的距离叫做椭圆的焦距.
2. 椭圆的标准方程:
(1)焦点在x轴上:
(a>b>0)
焦点坐标分别为(-c,0),(c,0).
(2)焦点在y轴上:
(a>b>0)
焦点坐标分别为(0,-c),(0,c).
课堂练习
1. 已知△ABC的顶点A,B在椭圆上,C在直线l:y=x+2上,且AB∥l.
(Ⅰ)当AB边通过坐标原点O时,求AB的长及△ABC的面积;
(Ⅱ)当∠ABC=90°,且斜边AC的长最大时,求AB所在直线的方程.
继续解答
解:(Ⅰ)因为AB∥l,且AB边通过点(0,0),所以AB所在直线的方程为y=x.
设A,B两点坐标分别为(x1,y1),(x2,y2).
由 得x=±1,
所以
又因为AB边上的高h等于原点到直线l的距离,所以
(Ⅱ)设AB所在直线的方程为y=x+m.
由 得 因为A,B在椭圆上,
所以
设A,B两点坐标分别为(x1,y1),(x2,y2).
则
所以 又因为BC的长等于点(0,m)到直线l的距离,即
所以 所以当m=-1时,AC边最长.
(这时△ =-12+64>0)
此时AB所在直线的方程为y=x-1.
(1)求椭圆C的方程; (2)若AB为垂直与x轴的动弦,直线l:x=4与x轴交于N,直线AF与BN交于点M.
①求证:点M恒在椭圆C上;
②求面积的最大值.
2. 如图,椭圆的一个焦点为F(1,0)且过点(2,0).
解:(1)由题设a=2,c=1,从而 所以方程为:
(2)①有F(1,0),N(4,0); 设A(m,n),则
B(m,-n),AF与BN得方程分别为:,
设交点M坐标为 ,则
;点M恒在椭圆C上
②设AM的方程为x=ty+1,带入 ,
得:
设 ,则有
则 ,
令 则
所以当 时, 有最大值3,此时AM过点F.
有最大值为 .
3. 如图、椭圆的一个焦点是F(1,0),O为坐标原点.
(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;
(Ⅱ)设过点F的直线l交椭圆于A、B两点.若直线l绕点F任意转动,值有,求a的取值范围.
解:(Ⅰ)设M,N为短轴的两个三等分点,因为△MNF为正三角形,所以, 即1= . 因此,椭圆方程为
(Ⅱ)设 (ⅰ)当直线 AB与x轴重合时,
(ⅱ)当直线AB不与x轴重合时,
设直线AB的方程为: 整理得 所以
因为有 ,所以∠AOB恒为钝角.
即 恒成立.
又a2+b2m2>0,所以-m2a2b2+b2-a2b2+a2<0对m ∈ R恒成立,
即a2b2m2> a2 -a2b2+b2对m ∈ R恒成立.
当m ∈ R时,a2b2m2最小值为0,所以 a2- a2b2+b2<0.
a2因为a>0,b>0,所以a0,
解得a> 或a< (舍去),a> ,
综合(i)(ii),a的取值范围为( ,+∞).
4. 填空题
(1)设是椭圆 上的一点,F1F2是椭圆的两个焦点,则 的最大值为 ;最小值为 .
4
1
(2)椭圆 的离心率为 ,则m= .
3或
5.选择题
(1)椭圆 的焦距是( )
A.2 B.
C. D.
(2)若椭圆的两焦点为(-2,0)和
(2,0),且椭圆过点 ,则椭圆
方程是( )
A. B.
C. D.
A
D
6.解答题
解: ∵e2=
∴椭圆方程可设为: 设A(x,y)是椭圆上任一点,则:│PA│2=x2+(y- )2=-3y2-3y+4b2+ f(y)(-b≤y≤b)
(1)设椭圆的中心是坐标原点,长轴在x轴上,离心率e= ,已知点P(0, )到椭圆上的点的最远距离是,求这个椭圆方程.
讨论:1°、-b>- 0<b< 时,│PA│ = f(-b)=(b+ )2
=
但b> ,矛盾.不合条件.
2°、-b≤- b≥ 时,│PA│ = f(- )=4b2+3=7 b2=1
∴所求椭圆为:
(2)椭圆的一个顶点为A(2,0),其长轴长是短轴长的2倍,求椭圆的标准方程.
解:(1)当 A(2,0)为 长轴端点时,
,
椭圆的标准方程为: ;
(2)当 A(2,0)为短轴端点时,
,
椭圆的标准方程为: ;
(3)求与椭圆 + =1有相等的焦距,且一条准线方程为12x-169=0的椭圆的标准方程.
解:c2=200-56=144,c=12,
又 = ,∴a=13,b=5.
故所求为 + =1.
人教B版 选修2-1 2.2.1 椭圆的标准方程
圆锥曲线与方程
教学目标
知识与能力:
理解椭圆的概念,掌握椭圆的定义、会用椭圆的定义解决实际问题;
理解椭圆标准方程的推导过程及化简无理方程的常用的方法;
了解求椭圆的动点的伴随点的轨迹方程的一般方法.
过程与方法:
注重数形结合,掌握解析法研究几何问题的一般方法;
注重探索能力的培养.
情感态度与价值观:
探究方法激发学生的求知欲,培养浓厚的学习兴趣;
进行数学美育的渗透,用哲学的观点指导学习.
教学重难点
椭圆定义的理解及标准方程的推导
重点:
难点:
标准方程的推导
从上述的探究中,我们可以知道:把细绳的两端拉开一段距离,移动笔尖的过程中,细绳的长度保持不变,即笔尖到两个定点的距离和等于常数.
椭圆:平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹.这两个定点叫做椭圆的焦点,两个焦点间的距离叫做椭圆的焦距.
y
x
M
F1
F2
O
c
c
图2.2-1
类比利用圆的对称性建立圆方程的过程,画出适当的坐标系,建立它的方程.
如图2.2-1,以经过两焦点F1,F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立直角坐标系xOy.
y
x
M
F1
F2
O
c
c
图2.2-1
设M(x,y)是椭圆上任意一点,椭圆的焦距为2c(c>0),那么焦点F1,F2的坐标分别为(-c,0)(c,0).又设M与F1,F2的距离等于2a.
由椭圆的定义,椭圆就是集合
P={M||MF1|+|MF2|=2a}.
因为|MF1|= ,|MF2|= ,
所以
化简此方程,将左边的一个根式移到右边,得:
将这个方程两边平方,得
整理得
上式两边再平方,得
a4-2a2cx+c2x2=a2x2-2a2cx+a2c2+a2y2,
整理得
(a2-c2)x2+a2y2=a2(a2-c2),
两边同除以a2(a2-c2),得
由椭圆的定义可知,2a>2c,即a>c,
所以,a2-c2>0.
①
y
x
P
F1
F2
O
图2.2-2
观察与分析
观察图2.2-2,你能从中找出表示a,c,
的线段吗?
由图可知,|PF1|=|PF2|=a,|OF1|=|OF2|=c,|PO|= , 令b=|PO|= ,那么①式就是
(a>b>0) ②
我们把方程②叫做椭圆的标准方程,椭圆上任意一点的坐标都满足此方程.它的焦点在x轴上,两个焦点分别是F1(-c,0),F2(c,0)这里的c2=a2-b2.
y
x
M
F1
F2
O
图2.2-3
如图2.2-3,如果焦点F1,F2在y轴上,且F1,F2的坐标分别为(0,-c),(0,c),a,b的意义同上,那么椭圆的方程是什么?
容易知道,此时椭圆的方程是
(a>b>0)
这个方程也是椭圆的标准方程.
例1:
已知椭圆的两个焦点坐标分别是(-2,0),(2,0),并且经过点 ,求它的标准方程.
解:因为椭圆的焦点在x轴上,所以设它的标准方程为
继续解答
(a>b>0).
由椭圆的定义知
所以
又因为c=2,所以b2=a2-c2=10-4=6.
因此,所求椭圆的标准方程为
例2:
中心在原点,一焦点为F1(0,5)的椭圆被直线y=3x-2截得的弦的中点横坐标是 ,求此椭圆的方程.
解:设椭圆的标准方程为:
(a>b>0),
则a2+b2=50…①
又设A(x1,y1),B(x2,y2),弦AB中点(x0,y0)
∵x0= ,∴y0= -2=-
继续解答
解①,②得:a2=75,b2=25,椭圆为:
×
由
…②
例3:
y
x
O
A
B
M
图 2.2-4
如图2.2-4,设点A,B的坐标分别为(-5,0),(5,0).直线AM,BM相交于点M,且它们的斜率之积是 ,求点M的轨迹方程.
分析
设点M的坐标为(x,y),那么直线AM,BM的斜率就可以用含有x,y的式子表示.由于直线AM,BM的斜率之积是 ,因此可以建立x,y之间的关系式,得出点M的轨迹方程.
解:设点M的坐标为(x,y),因为点A的坐标是(-5,0),所以,直线AM的斜率为
继续解答
(x ≠ -5);
同理,直线BM的斜率
(x ≠ 5).
由已知有
(x≠±5)
化简,得点M的轨迹方程为
( x≠±5 ).
课堂小结
1. 椭圆:
平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹.这两个定点叫做椭圆的焦点,两个焦点间的距离叫做椭圆的焦距.
2. 椭圆的标准方程:
(1)焦点在x轴上:
(a>b>0)
焦点坐标分别为(-c,0),(c,0).
(2)焦点在y轴上:
(a>b>0)
焦点坐标分别为(0,-c),(0,c).
课堂练习
1. 已知△ABC的顶点A,B在椭圆上,C在直线l:y=x+2上,且AB∥l.
(Ⅰ)当AB边通过坐标原点O时,求AB的长及△ABC的面积;
(Ⅱ)当∠ABC=90°,且斜边AC的长最大时,求AB所在直线的方程.
继续解答
解:(Ⅰ)因为AB∥l,且AB边通过点(0,0),所以AB所在直线的方程为y=x.
设A,B两点坐标分别为(x1,y1),(x2,y2).
由 得x=±1,
所以
又因为AB边上的高h等于原点到直线l的距离,所以
(Ⅱ)设AB所在直线的方程为y=x+m.
由 得 因为A,B在椭圆上,
所以
设A,B两点坐标分别为(x1,y1),(x2,y2).
则
所以 又因为BC的长等于点(0,m)到直线l的距离,即
所以 所以当m=-1时,AC边最长.
(这时△ =-12+64>0)
此时AB所在直线的方程为y=x-1.
(1)求椭圆C的方程; (2)若AB为垂直与x轴的动弦,直线l:x=4与x轴交于N,直线AF与BN交于点M.
①求证:点M恒在椭圆C上;
②求面积的最大值.
2. 如图,椭圆的一个焦点为F(1,0)且过点(2,0).
解:(1)由题设a=2,c=1,从而 所以方程为:
(2)①有F(1,0),N(4,0); 设A(m,n),则
B(m,-n),AF与BN得方程分别为:,
设交点M坐标为 ,则
;点M恒在椭圆C上
②设AM的方程为x=ty+1,带入 ,
得:
设 ,则有
则 ,
令 则
所以当 时, 有最大值3,此时AM过点F.
有最大值为 .
3. 如图、椭圆的一个焦点是F(1,0),O为坐标原点.
(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;
(Ⅱ)设过点F的直线l交椭圆于A、B两点.若直线l绕点F任意转动,值有,求a的取值范围.
解:(Ⅰ)设M,N为短轴的两个三等分点,因为△MNF为正三角形,所以, 即1= . 因此,椭圆方程为
(Ⅱ)设 (ⅰ)当直线 AB与x轴重合时,
(ⅱ)当直线AB不与x轴重合时,
设直线AB的方程为: 整理得 所以
因为有 ,所以∠AOB恒为钝角.
即 恒成立.
又a2+b2m2>0,所以-m2a2b2+b2-a2b2+a2<0对m ∈ R恒成立,
即a2b2m2> a2 -a2b2+b2对m ∈ R恒成立.
当m ∈ R时,a2b2m2最小值为0,所以 a2- a2b2+b2<0.
a2
解得a> 或a< (舍去),a> ,
综合(i)(ii),a的取值范围为( ,+∞).
4. 填空题
(1)设是椭圆 上的一点,F1F2是椭圆的两个焦点,则 的最大值为 ;最小值为 .
4
1
(2)椭圆 的离心率为 ,则m= .
3或
5.选择题
(1)椭圆 的焦距是( )
A.2 B.
C. D.
(2)若椭圆的两焦点为(-2,0)和
(2,0),且椭圆过点 ,则椭圆
方程是( )
A. B.
C. D.
A
D
6.解答题
解: ∵e2=
∴椭圆方程可设为: 设A(x,y)是椭圆上任一点,则:│PA│2=x2+(y- )2=-3y2-3y+4b2+ f(y)(-b≤y≤b)
(1)设椭圆的中心是坐标原点,长轴在x轴上,离心率e= ,已知点P(0, )到椭圆上的点的最远距离是,求这个椭圆方程.
讨论:1°、-b>- 0<b< 时,│PA│ = f(-b)=(b+ )2
=
但b> ,矛盾.不合条件.
2°、-b≤- b≥ 时,│PA│ = f(- )=4b2+3=7 b2=1
∴所求椭圆为:
(2)椭圆的一个顶点为A(2,0),其长轴长是短轴长的2倍,求椭圆的标准方程.
解:(1)当 A(2,0)为 长轴端点时,
,
椭圆的标准方程为: ;
(2)当 A(2,0)为短轴端点时,
,
椭圆的标准方程为: ;
(3)求与椭圆 + =1有相等的焦距,且一条准线方程为12x-169=0的椭圆的标准方程.
解:c2=200-56=144,c=12,
又 = ,∴a=13,b=5.
故所求为 + =1.
