人教B版 选修2-1 高中数学 2.2.2椭圆的几何性质(共39张PPT)
文档属性
| 名称 | 人教B版 选修2-1 高中数学 2.2.2椭圆的几何性质(共39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-08 20:38:39 | ||
图片预览









文档简介
(共39张PPT)
人教B版 选修2-1 2.2.2 椭圆的几何性质
圆锥曲线与方程
教学目标
知识与能力:
了解用方程的方法研究图形的对称性;
理解椭圆的范围、对称性及对称轴,对称中心、离心率、顶点的概念;
掌握椭圆的标准方程、会用椭圆的定义解决实际问题;
过程与方法:
注重数形结合,掌握解析法研究几何问题的一般方法,注重培养学生的能力;
注重探索能力的培养.
情感态度与价值观:
在合作、互动的教学氛围中,培养学生科学探索精神,激励学生创新.
让学生参与利用信息技术探究点的轨迹问题,培养学生学习数学的兴趣.
教学重难点
重点:
难点:
认识生活中的椭圆,及其特点.
掌握椭圆的简单几何性质.
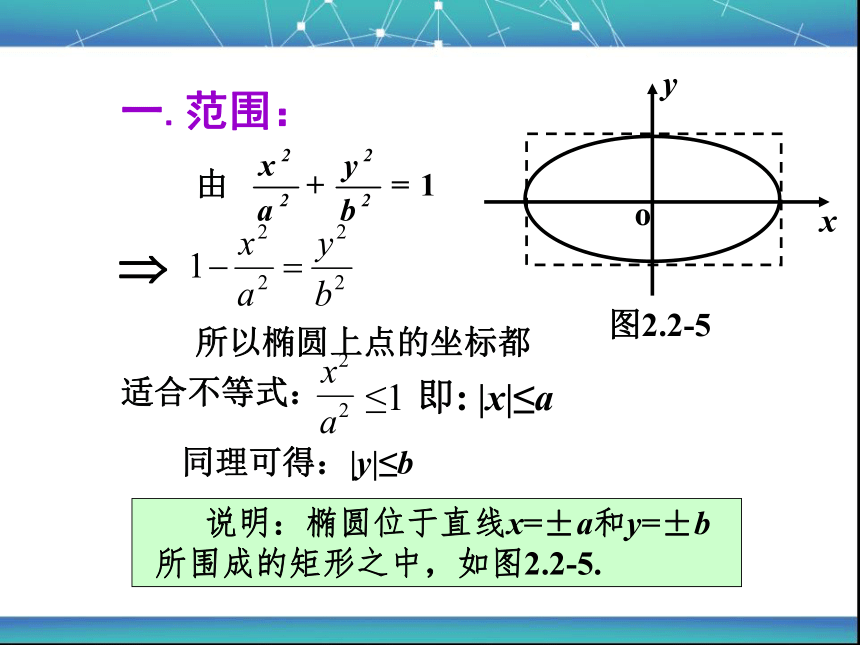
一.范围:
o
x
y
图2.2-5
由
同理可得:|y|≤b
说明:椭圆位于直线x=±a和y=±b所围成的矩形之中,如图2.2-5.
所以椭圆上点的坐标都适合不等式:
≤1
即: |x|≤a
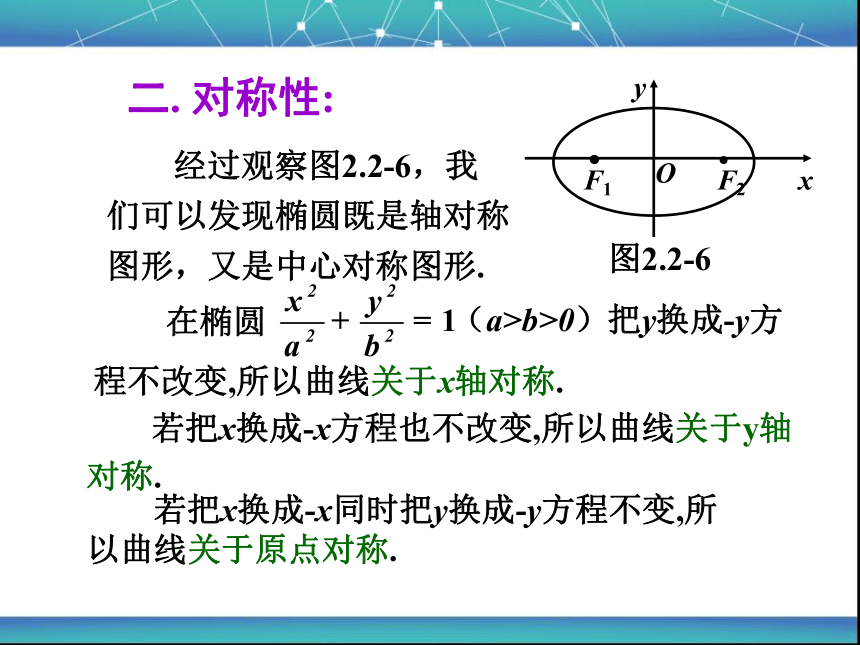
二. 对称性:
?
F1
?
F2
x
y
O
图2.2-6
经过观察图2.2-6,我们可以发现椭圆既是轴对称图形,又是中心对称图形.
在椭圆
(a>b>0)把y换成-y方
程不改变,所以曲线关于x轴对称.
若把x换成-x方程也不改变,所以曲线关于y轴对称.
若把x换成-x同时把y换成-y方程不变,所以曲线关于原点对称.
结论
由上述可知,椭圆关于x轴、y轴对称,坐标轴就是椭圆的对称轴,原点是椭圆的对称中心.对称中心叫做椭圆的中心.
三. 顶点:
在椭圆
(a>b>0)中,令x=0,
那么y= ,
说明椭圆与 y轴的交点是(0, ±b )
±b
令 y=0,得 x= ,
说明椭圆与 x轴的交点是
±a
椭圆和对称轴的交点叫做椭圆的顶点.
如右图,椭圆与对称轴有四个交点:A1、A2、B1、B2
o
x
y
B1(0,b)
B2(0,-b)
A1
A2
(±a ,0 ).
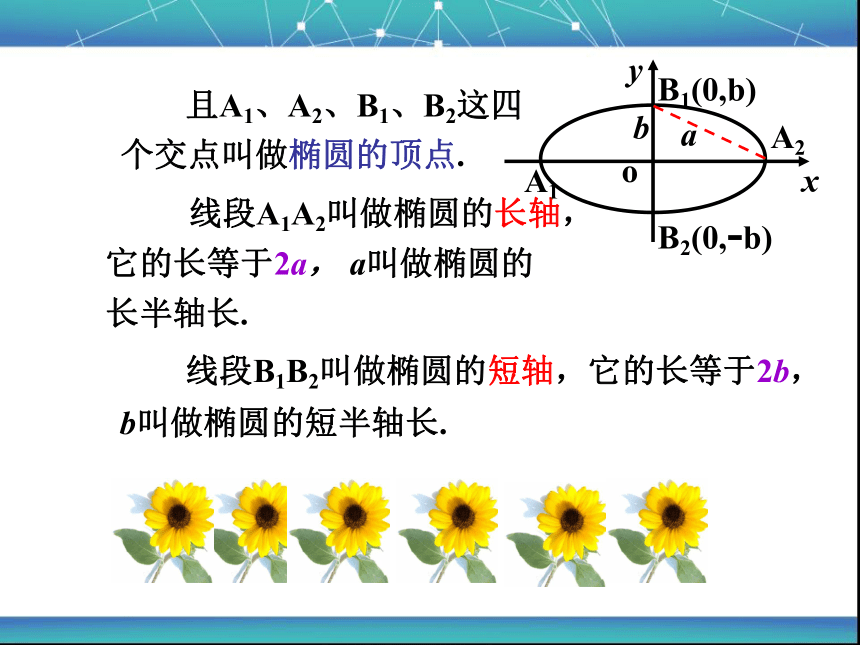
且A1、A2、B1、B2这四个交点叫做椭圆的顶点.
线段A1A2叫做椭圆的长轴,它的长等于2a, a叫做椭圆的长半轴长.
线段B1B2叫做椭圆的短轴,它的长等于2b, b叫做椭圆的短半轴长.
o
x
y
B1(0,b)
B2(0,-b)
A1
A2
a
b
四. 离心率:
图2.2-6
观察图2.2-6,我们发现椭圆的扁平程度不一,那么用什么量可以刻画椭圆的扁平程度呢?
我们接下来讲的离心率就可以刻画.
离心率:椭圆的焦距与长轴长的比 叫做离心率. 用e表示,记做e= .
y
x
O
图2.2-7
如图2.2-7,椭圆
(a>b>0)
的长半轴为a,半焦距为c.保持长半轴a不变,改变椭圆的半焦距c,可以发现,c越接近a,椭圆越扁平.所以用a、c这两个量可以刻画椭圆的扁平程度.
1. 离心率的取值范围:
因为a>c> 0,所以1>e>0.
2. 离心率对椭圆形状的影响:
1)e 越接近 1, c 就越接近 a, 从而 b就越小, 椭 圆就越扁.
2)e 越接近 0, c 就越接近 0, 从而 b就越大, 椭 圆就越圆.
3)当且仅当a=b时,c=0,这时这两个焦点重合,图形变成圆,它的方程为x2+y2=a2.
例1:
解:由方程可知,a=4,b=3,则c=
求椭圆 的离心率、顶点坐标.
所以这个椭圆的离心率e=
顶点坐标为A1(4,0),A2(-4,0),B1(0,3),B2(0,-3)
例2:
求满足长轴与短轴之和为20,焦距为
的椭圆方程.
解:当焦点在x轴上时,
设所求椭圆的方程为
由题意,得
即
解得a=6,b=4
继续解答
所以焦点在x轴上的椭圆的方程为
同理可求当焦点在y轴上椭圆的方程为
因此,所求的椭圆的方程为
和
例3:
l
y
x
O
F
.
M
d
H
∟
图2.2-8
点M(x,y)与定点F(4,0)的距离和它到直线l: 的距离的比是常数 ,求点M的轨迹.
解:设d是点M到直线l: 的距离,根据题意,点M的轨迹就是集合
继续解答
由此得
将上式两边平方,并化简,得9x2+25y2=225,
即
所以,点M的轨迹是长轴、短轴分别为10、6的椭圆.(图2.2-8)
l
y
x
O
F
.
M
d
H
∟
图2.2-8
课堂小结
1. 范围:
椭圆 (a>b>0)位于直线x=±a和y=±b所围成的矩形框内.
2. 对称性:
椭圆关于x轴、y轴都是对称的,坐标轴是椭圆的对称轴,原点是椭圆的对称中心,椭圆的对称中心是椭圆的中心.
3. 顶点:
椭圆与它的对称轴x轴,y轴的四个交点叫做椭圆的顶点.
o
x
y
B1(0,b)
B2(0,-b)
A1
A2
椭圆 顶点坐标分别为A1(-a,0),A2(a,0),B1(0,-b),B2(0,b)如图所示.
4. 离心率
把椭圆的焦距与长轴长的比 称为椭圆的离心率,用e表示,即e= ,取值范围为0离心率对椭圆形状的影响:
1)e 越接近 1, c 就越接近 a, 从而 b就越小, 椭 圆就越扁.
2)e 越接近 0, c 就越接近 0, 从而 b就越大, 椭 圆就越圆.
3)当且仅当a=b时,c=0,这时这两个焦点重合,图形变成圆,它的方程为x2+y2=a2.
课堂练习
1. 设椭圆 (a>b>0)的左右焦点分别为F1,F2,离心率 ,右准线为l,M,N是l上的两个动点,
(Ⅰ)若 ,求a,b的值;
(Ⅱ)证明:当|MN|取最小值时, 与
共线.
解:由a2-b2=c2与 ,得 a2=2b2 ,
,l的方程为
设
则
由
得
①
(Ⅰ)由
,得
②
③
由①、②、③三式,消去y1,y2,并求得a2=4 故
(Ⅱ)
当且仅当
或
时,
|MN|取最小值
此时,
故
与
共线.
2 . 已知△ABC的顶点A,B在椭圆 上,C在直线l:y=x+2上,且AB∥l.
(Ⅰ)当AB边通过坐标原点O时,求AB的长及△ABC的面积;
(Ⅱ)当∠ABC=90°,且斜边AC的长最大时,求AB所在直线的方程.
解:(Ⅰ)因为AB∥l,且AB边通过点(0,0),所以AB所在直线的方程为y=x.
设A,B两点坐标分别为(x1,y1),(x2,y2).
由
得
所以
又因为AB边上的高h等于原点到直线l的距离,
所以 h= ,S△ABC= |AB|·h=2
(Ⅱ)设AB所在直线的方程为y=x+m.
由
得
因为A,B在椭圆上,所以
设A,B两点坐标分别为(x1,y1),(x2,y2).
则
所以
又因为BC的长等于点(0,m)到直线l的距离,即
所以
所以当m=-1时,AC边最长.(这时△=-12+64>0)
此时AB所在直线的方程为y=x-1.
3. 设椭圆 (a>b>0)过点 ,且着焦点为
(Ⅰ)求椭圆C的方程;
(Ⅱ)当过点 的动直线l与椭圆C相交与两不同点A,B时,在线段A,B上取点Q,满足|AP|·|QB|=|AQ|·|PB|,证明:点Q总在某定直线上.
解:(1)由题意: ,解得 ,
所求椭圆方程为
(2)设点Q、A、B的坐标分别为
由题设知
均不为零,记
则
且
又A,P,B,Q四点共线,从而
于是
从而
……(1)
……(2)
又点A、B在椭圆C上,即
(1)+(2)×2并结合(3),(4)得
即 点总在定直线 上.
4.填空题
(1)已知椭圆中心在原点,一个焦点是F (-2 ,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是_____________.
(2)分别是椭圆的左右焦点,AB为其过点且斜率为1的弦,则的值为 _________.
5.选择题
(1)方程表示焦点在y轴上的椭圆,则k的取值范围是( )
A.(0,+∞) B.(0,2) C.(1,+∞) D.(0,1)
D
(2)若椭圆两准线间的距离等于焦距的4倍,则这个椭圆的离心率为 ( )
A. B. C. D.
D
6.解答题
(1)椭圆 (a >b>0)与直线x+y=1交于P、Q两点,且 ,其中O为坐标原点.
Ⅰ.求 的值;
Ⅱ.若椭圆的离心率e满足 ≤e≤ ,求椭圆长轴的取值范围.
解:设P(x1,y1),由OP ⊥ OQ
x 1 x 2 + y 1 y 2 = 0
又将y=1-x代入,
①
代入①化简得
Ⅱ. 又由Ⅰ.知 ,
∴长轴 2a ∈ [ ].
(2)中心在原点,一焦点为F1(0,5 )的椭圆被直线y=3x-2截得的弦的中点横坐标是 ,求此椭圆的方程.
解:设椭圆: (a>b>0),
则a2+b2=50…①
又设A(x1,y1),B(x2,y2),弦AB中点(x0,y0)
∵x0= ,∴y0= -2=-
由
②
解①,②得:a2=75,b2=25,椭圆为:
(3)椭圆C: (a>b>0)的两个焦点为F1,F2,点P在椭圆C上,且PF1⊥F1F2,|PF1|= ,|PF2|= .
Ⅰ. 求椭圆C的方程;
Ⅱ. 若直线l过圆x2+y2+4x-2y=0的圆心M,交椭圆C于A,B两点,且A,B关于点M对称,求直线l的方程.
解: Ⅰ.用椭圆定义及基本量法可以求得椭圆方程为 ;
Ⅱ.设A(x1,y1)、B(x2,y2),直线l过点M(-2,1),设直线方程为y=k(x+2)+1,代入椭圆方程得(4+9k2)x2+(36k2+18k)x+36k2+36k-27=0,由已知得A,B关于M(-2,1)对称,故
,解得k= ,所求直线方程为8x-9y+25=0,经检验所求直线方程符合题意.
人教B版 选修2-1 2.2.2 椭圆的几何性质
圆锥曲线与方程
教学目标
知识与能力:
了解用方程的方法研究图形的对称性;
理解椭圆的范围、对称性及对称轴,对称中心、离心率、顶点的概念;
掌握椭圆的标准方程、会用椭圆的定义解决实际问题;
过程与方法:
注重数形结合,掌握解析法研究几何问题的一般方法,注重培养学生的能力;
注重探索能力的培养.
情感态度与价值观:
在合作、互动的教学氛围中,培养学生科学探索精神,激励学生创新.
让学生参与利用信息技术探究点的轨迹问题,培养学生学习数学的兴趣.
教学重难点
重点:
难点:
认识生活中的椭圆,及其特点.
掌握椭圆的简单几何性质.
一.范围:
o
x
y
图2.2-5
由
同理可得:|y|≤b
说明:椭圆位于直线x=±a和y=±b所围成的矩形之中,如图2.2-5.
所以椭圆上点的坐标都适合不等式:
≤1
即: |x|≤a
二. 对称性:
?
F1
?
F2
x
y
O
图2.2-6
经过观察图2.2-6,我们可以发现椭圆既是轴对称图形,又是中心对称图形.
在椭圆
(a>b>0)把y换成-y方
程不改变,所以曲线关于x轴对称.
若把x换成-x方程也不改变,所以曲线关于y轴对称.
若把x换成-x同时把y换成-y方程不变,所以曲线关于原点对称.
结论
由上述可知,椭圆关于x轴、y轴对称,坐标轴就是椭圆的对称轴,原点是椭圆的对称中心.对称中心叫做椭圆的中心.
三. 顶点:
在椭圆
(a>b>0)中,令x=0,
那么y= ,
说明椭圆与 y轴的交点是(0, ±b )
±b
令 y=0,得 x= ,
说明椭圆与 x轴的交点是
±a
椭圆和对称轴的交点叫做椭圆的顶点.
如右图,椭圆与对称轴有四个交点:A1、A2、B1、B2
o
x
y
B1(0,b)
B2(0,-b)
A1
A2
(±a ,0 ).
且A1、A2、B1、B2这四个交点叫做椭圆的顶点.
线段A1A2叫做椭圆的长轴,它的长等于2a, a叫做椭圆的长半轴长.
线段B1B2叫做椭圆的短轴,它的长等于2b, b叫做椭圆的短半轴长.
o
x
y
B1(0,b)
B2(0,-b)
A1
A2
a
b
四. 离心率:
图2.2-6
观察图2.2-6,我们发现椭圆的扁平程度不一,那么用什么量可以刻画椭圆的扁平程度呢?
我们接下来讲的离心率就可以刻画.
离心率:椭圆的焦距与长轴长的比 叫做离心率. 用e表示,记做e= .
y
x
O
图2.2-7
如图2.2-7,椭圆
(a>b>0)
的长半轴为a,半焦距为c.保持长半轴a不变,改变椭圆的半焦距c,可以发现,c越接近a,椭圆越扁平.所以用a、c这两个量可以刻画椭圆的扁平程度.
1. 离心率的取值范围:
因为a>c> 0,所以1>e>0.
2. 离心率对椭圆形状的影响:
1)e 越接近 1, c 就越接近 a, 从而 b就越小, 椭 圆就越扁.
2)e 越接近 0, c 就越接近 0, 从而 b就越大, 椭 圆就越圆.
3)当且仅当a=b时,c=0,这时这两个焦点重合,图形变成圆,它的方程为x2+y2=a2.
例1:
解:由方程可知,a=4,b=3,则c=
求椭圆 的离心率、顶点坐标.
所以这个椭圆的离心率e=
顶点坐标为A1(4,0),A2(-4,0),B1(0,3),B2(0,-3)
例2:
求满足长轴与短轴之和为20,焦距为
的椭圆方程.
解:当焦点在x轴上时,
设所求椭圆的方程为
由题意,得
即
解得a=6,b=4
继续解答
所以焦点在x轴上的椭圆的方程为
同理可求当焦点在y轴上椭圆的方程为
因此,所求的椭圆的方程为
和
例3:
l
y
x
O
F
.
M
d
H
∟
图2.2-8
点M(x,y)与定点F(4,0)的距离和它到直线l: 的距离的比是常数 ,求点M的轨迹.
解:设d是点M到直线l: 的距离,根据题意,点M的轨迹就是集合
继续解答
由此得
将上式两边平方,并化简,得9x2+25y2=225,
即
所以,点M的轨迹是长轴、短轴分别为10、6的椭圆.(图2.2-8)
l
y
x
O
F
.
M
d
H
∟
图2.2-8
课堂小结
1. 范围:
椭圆 (a>b>0)位于直线x=±a和y=±b所围成的矩形框内.
2. 对称性:
椭圆关于x轴、y轴都是对称的,坐标轴是椭圆的对称轴,原点是椭圆的对称中心,椭圆的对称中心是椭圆的中心.
3. 顶点:
椭圆与它的对称轴x轴,y轴的四个交点叫做椭圆的顶点.
o
x
y
B1(0,b)
B2(0,-b)
A1
A2
椭圆 顶点坐标分别为A1(-a,0),A2(a,0),B1(0,-b),B2(0,b)如图所示.
4. 离心率
把椭圆的焦距与长轴长的比 称为椭圆的离心率,用e表示,即e= ,取值范围为0
1)e 越接近 1, c 就越接近 a, 从而 b就越小, 椭 圆就越扁.
2)e 越接近 0, c 就越接近 0, 从而 b就越大, 椭 圆就越圆.
3)当且仅当a=b时,c=0,这时这两个焦点重合,图形变成圆,它的方程为x2+y2=a2.
课堂练习
1. 设椭圆 (a>b>0)的左右焦点分别为F1,F2,离心率 ,右准线为l,M,N是l上的两个动点,
(Ⅰ)若 ,求a,b的值;
(Ⅱ)证明:当|MN|取最小值时, 与
共线.
解:由a2-b2=c2与 ,得 a2=2b2 ,
,l的方程为
设
则
由
得
①
(Ⅰ)由
,得
②
③
由①、②、③三式,消去y1,y2,并求得a2=4 故
(Ⅱ)
当且仅当
或
时,
|MN|取最小值
此时,
故
与
共线.
2 . 已知△ABC的顶点A,B在椭圆 上,C在直线l:y=x+2上,且AB∥l.
(Ⅰ)当AB边通过坐标原点O时,求AB的长及△ABC的面积;
(Ⅱ)当∠ABC=90°,且斜边AC的长最大时,求AB所在直线的方程.
解:(Ⅰ)因为AB∥l,且AB边通过点(0,0),所以AB所在直线的方程为y=x.
设A,B两点坐标分别为(x1,y1),(x2,y2).
由
得
所以
又因为AB边上的高h等于原点到直线l的距离,
所以 h= ,S△ABC= |AB|·h=2
(Ⅱ)设AB所在直线的方程为y=x+m.
由
得
因为A,B在椭圆上,所以
设A,B两点坐标分别为(x1,y1),(x2,y2).
则
所以
又因为BC的长等于点(0,m)到直线l的距离,即
所以
所以当m=-1时,AC边最长.(这时△=-12+64>0)
此时AB所在直线的方程为y=x-1.
3. 设椭圆 (a>b>0)过点 ,且着焦点为
(Ⅰ)求椭圆C的方程;
(Ⅱ)当过点 的动直线l与椭圆C相交与两不同点A,B时,在线段A,B上取点Q,满足|AP|·|QB|=|AQ|·|PB|,证明:点Q总在某定直线上.
解:(1)由题意: ,解得 ,
所求椭圆方程为
(2)设点Q、A、B的坐标分别为
由题设知
均不为零,记
则
且
又A,P,B,Q四点共线,从而
于是
从而
……(1)
……(2)
又点A、B在椭圆C上,即
(1)+(2)×2并结合(3),(4)得
即 点总在定直线 上.
4.填空题
(1)已知椭圆中心在原点,一个焦点是F (-2 ,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是_____________.
(2)分别是椭圆的左右焦点,AB为其过点且斜率为1的弦,则的值为 _________.
5.选择题
(1)方程表示焦点在y轴上的椭圆,则k的取值范围是( )
A.(0,+∞) B.(0,2) C.(1,+∞) D.(0,1)
D
(2)若椭圆两准线间的距离等于焦距的4倍,则这个椭圆的离心率为 ( )
A. B. C. D.
D
6.解答题
(1)椭圆 (a >b>0)与直线x+y=1交于P、Q两点,且 ,其中O为坐标原点.
Ⅰ.求 的值;
Ⅱ.若椭圆的离心率e满足 ≤e≤ ,求椭圆长轴的取值范围.
解:设P(x1,y1),由OP ⊥ OQ
x 1 x 2 + y 1 y 2 = 0
又将y=1-x代入,
①
代入①化简得
Ⅱ. 又由Ⅰ.知 ,
∴长轴 2a ∈ [ ].
(2)中心在原点,一焦点为F1(0,5 )的椭圆被直线y=3x-2截得的弦的中点横坐标是 ,求此椭圆的方程.
解:设椭圆: (a>b>0),
则a2+b2=50…①
又设A(x1,y1),B(x2,y2),弦AB中点(x0,y0)
∵x0= ,∴y0= -2=-
由
②
解①,②得:a2=75,b2=25,椭圆为:
(3)椭圆C: (a>b>0)的两个焦点为F1,F2,点P在椭圆C上,且PF1⊥F1F2,|PF1|= ,|PF2|= .
Ⅰ. 求椭圆C的方程;
Ⅱ. 若直线l过圆x2+y2+4x-2y=0的圆心M,交椭圆C于A,B两点,且A,B关于点M对称,求直线l的方程.
解: Ⅰ.用椭圆定义及基本量法可以求得椭圆方程为 ;
Ⅱ.设A(x1,y1)、B(x2,y2),直线l过点M(-2,1),设直线方程为y=k(x+2)+1,代入椭圆方程得(4+9k2)x2+(36k2+18k)x+36k2+36k-27=0,由已知得A,B关于M(-2,1)对称,故
,解得k= ,所求直线方程为8x-9y+25=0,经检验所求直线方程符合题意.
