人教B版 选修2-1 高中数学 第三章 3.1.3两个向量的数量积 教学课件(共34张PPT)
文档属性
| 名称 | 人教B版 选修2-1 高中数学 第三章 3.1.3两个向量的数量积 教学课件(共34张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-08 20:39:25 | ||
图片预览









文档简介
(共34张PPT)
导入新课
复习
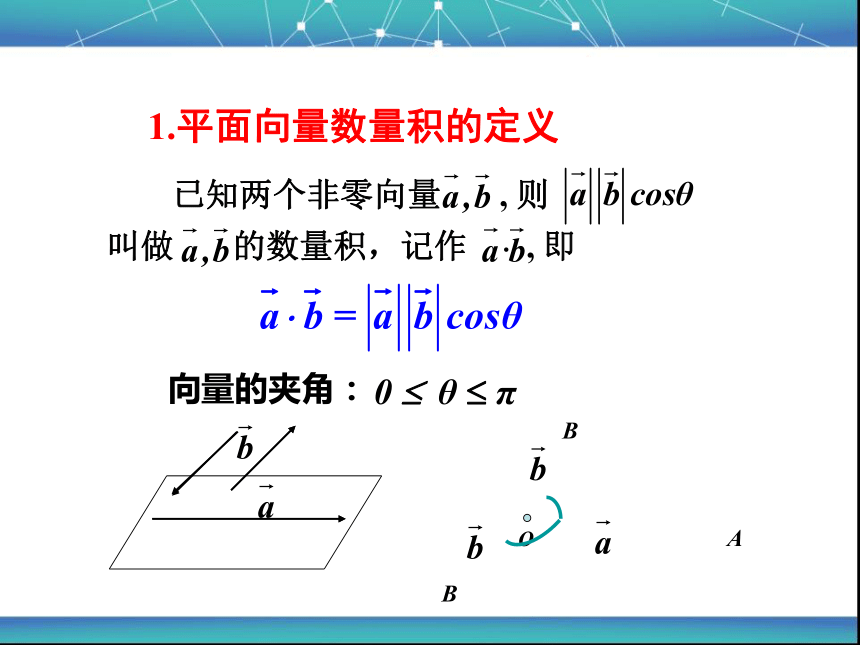
如果一个物体在力F的作用下产生位移s,那么力F所作的功 ,为了在数学中体现“功”的这样一个标量,我们引入了“数量积”的概念.
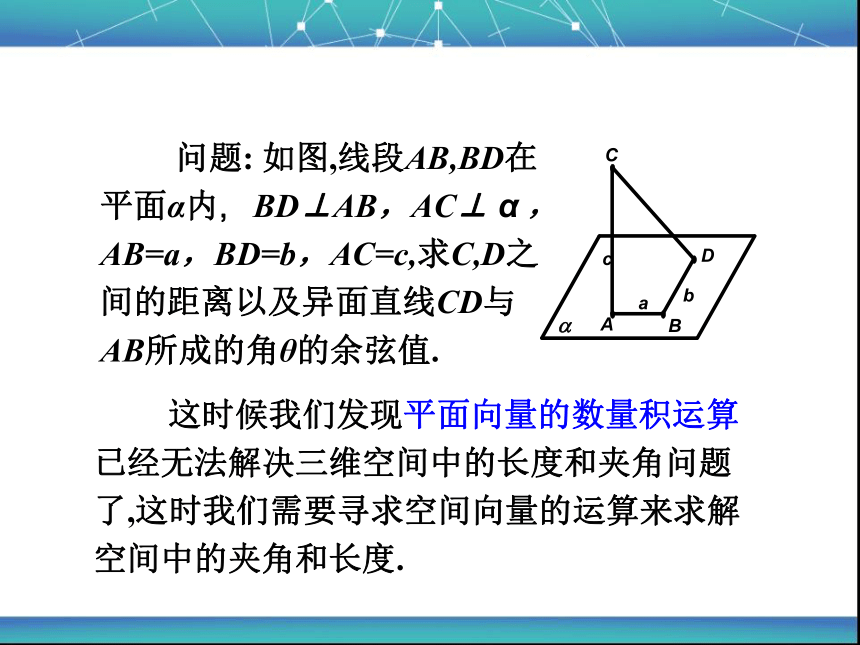
1.平面向量数量积的定义
已知两个非零向量 , 则
叫做 的数量积,记作 , 即
O
A
B
向量的夹角:
B
2.平面向量的数量积的主要性质
设a,b是两个非零向量
(1)a⊥b a×b=0数量积为零是判定两非零向量垂直的充要条件;
(2)当a与b同向时, a·b=|a|·|b|;当a与b反向时, a·b=-|a|·|b|;特别地, 用于计算向量的模;
(3) 用于计算向量的夹角.
3.平面向量数量积满足的运算律
(1)交换律:
(2)对数乘的结合律:
(3)分配律:
数量积不满足结合律,即:
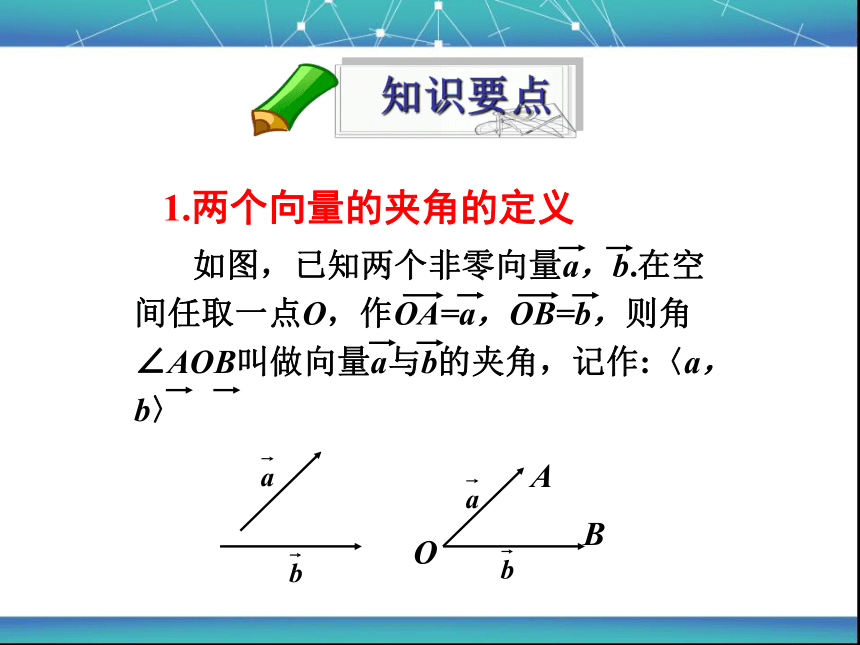
问题: 如图,线段AB,BD在平面α内,BD⊥AB,AC⊥ α ,AB=a,BD=b,AC=c,求C,D之间的距离以及异面直线CD与AB所成的角θ的余弦值.
这时候我们发现平面向量的数量积运算已经无法解决三维空间中的长度和夹角问题了,这时我们需要寻求空间向量的运算来求解空间中的夹角和长度.
3.1.3两个向量的数量积
教学目标
知识目标
(1)掌握空间向量的数量积公式及向量的夹角公式;
(2)运用公式解决立体几何中的有关问题.
能力目标
(1) 比较平面、空间向量,培养学生观察、分析、类比转化的能力;
(2)探究空间几何图形,将几何问题代数化,提高分析问题、解决问题的能力.
情感目标
(1)通过师生的合作与交流,体现教师为主导、学生为主体的教学模式;
(2)通过空间向量在立体几何中的应用,提高学生的空间想象力,培养学生探索精神和创新意识,让学生感受数学,体会数学美的魅力,激发学生学数学、用数学的热情.
教学重难点
重点
难点
空间向量数量积公式及其应用.
(1)如何将立体几何问题等价转化为向量问题;
(2)在此基础上,通过向量运算解决立体几何问题.
知识要点
1.两个向量的夹角的定义
如图,已知两个非零向量a,b.在空间任取一点O,作OA=a,OB=b,则角∠AOB叫做向量a与b的夹角,记作:〈a,b〉
O
A
B
范围:0≤〈a,b〉≤π在这个规定下,两个向量的夹角就被唯一确定了,并且〈a,b〉= 〈b,a〉.
如果〈a,b〉= π/2,则称a与b互相垂直,并记作a⊥b .
2. 空间向量数量积的定义
设OA=a,则有向线段OA的长度叫做向量a的长度或模,记作: | a |
已知空间两个非零向量 , 则
叫做 的数量积,记作 , 即
(1)两个向量的数量积是数量,而不是向量.
(2)规定:零向量与任意向量的数量积等于零.
(3)
3.空间向量数量积的运算律
(交换律)
(分配律)
思考!
吗?
(2)对于向量 , 成立吗?
若m、n是平面α内的两条相交直线,且l⊥m, l⊥n. 则l ⊥α.
g
l
m
n
4.线面垂直的判定定理:
已知m,n是平面?内的两条相交直线,直线l与?的交点为B,且l⊥m,l⊥n,
求证:l⊥? .
例题1
n
m
g
g
m
n
?
l
l
分析:由定义可知,只需证l与平面内任意直线g垂直.
要证l与g垂直,只需证l·g=0
而m,n不平行,由共面向量定理知,存在唯一的有序实数对(x,y)使得 g=xm+yn
要证l·g=0,只需l· g= xl·m+yl·n=0
而l·m=0 ,l·n=0
故 l·g=0
在?内作不与m、n重合的任一条直线g,在l、m、n、g上取非零向量l、m、n、g,因m与n相交,得向量m、n不平行.
由共面向量定理可知,存在唯一的有序实数对(x,y),使
g=xm+yn, l·g=xl·m+yl·n
证明
∵ l·m=0, l·n=0
∴ l·g=0
∴ l⊥g
∴ l⊥g
这就证明了直线l垂直于平面?内的任一条直线,所以l⊥? .
继续
例题2
已知空间四边形ABCD的每条边和对角线的长都等于a,点M、N分别是边AB、CD的中点.
求证:MN⊥AB,MN⊥CD .
证明
因为
所以
同理,
已知:在空间四边形OABC中,OA⊥BC,OB⊥AC,求证:OC⊥AB.
例题3
A
B
C
O
继续
课堂小结
1.空间向量数量积的概念.
2.探究空间向量数量积运算的性质.
3.空间向量的运算律.
4.空间向量数量积的应用.
5. 通过学习,体会到我们可以利用向量数量积解决立体几何中的以下问题
(1)证明两直线垂直;
(2)求两点之间的距离或线段长度;
(3)证明线面垂直;
(4)求两直线所成角的余弦值等等.
(1)已知向量a,b满足| a |=1,| b |=2,|a - b|=3,则|a + b|=_________.
课堂练习
1.填空
1
方法一:发现|a + b|2+|a –b |2=2(| a |2+| b |2)带入求得.
有其他方法吗?
方法二:由|a –b|2=| a |2 - 2a·b + | b |2
带入求得a·b=-2.
∴|a + b|2=| a |2+2a·b+| b |2
得 |a+b|=1
方法三:数形结合法,发现形的特殊性.
继续
(2)已知 则a,b所成的夹角为_______.
分析:根据两向量夹角公式
可得到所求结果.
2.选择
设a,b,c是任意的非零空间向量,且相互不共线,则:
①(a·b)c-(c·a)b=0 ②|a|-|b|<|a-b|
③(b·c)a-(c·a)b不与c垂直
④(3a+2b)·(3a-2b)=9|a|2-4|b|2
中,真命题是( )
A. ①② B. ②③ C. ③④ D. ②④
D
3.解答题
如图,在平行六面体ABCD-A’B’C’D’ 中,E,F,G分别是A’D’,D’D,D’C’的中点,请选择恰当的基底向量证明:
①EG//AC
②平面EFG//平面AB’C
证明
取基底:
①
②
由①知
∴平面EFG//平面AB’C.
继续
导入新课
复习
如果一个物体在力F的作用下产生位移s,那么力F所作的功 ,为了在数学中体现“功”的这样一个标量,我们引入了“数量积”的概念.
1.平面向量数量积的定义
已知两个非零向量 , 则
叫做 的数量积,记作 , 即
O
A
B
向量的夹角:
B
2.平面向量的数量积的主要性质
设a,b是两个非零向量
(1)a⊥b a×b=0数量积为零是判定两非零向量垂直的充要条件;
(2)当a与b同向时, a·b=|a|·|b|;当a与b反向时, a·b=-|a|·|b|;特别地, 用于计算向量的模;
(3) 用于计算向量的夹角.
3.平面向量数量积满足的运算律
(1)交换律:
(2)对数乘的结合律:
(3)分配律:
数量积不满足结合律,即:
问题: 如图,线段AB,BD在平面α内,BD⊥AB,AC⊥ α ,AB=a,BD=b,AC=c,求C,D之间的距离以及异面直线CD与AB所成的角θ的余弦值.
这时候我们发现平面向量的数量积运算已经无法解决三维空间中的长度和夹角问题了,这时我们需要寻求空间向量的运算来求解空间中的夹角和长度.
3.1.3两个向量的数量积
教学目标
知识目标
(1)掌握空间向量的数量积公式及向量的夹角公式;
(2)运用公式解决立体几何中的有关问题.
能力目标
(1) 比较平面、空间向量,培养学生观察、分析、类比转化的能力;
(2)探究空间几何图形,将几何问题代数化,提高分析问题、解决问题的能力.
情感目标
(1)通过师生的合作与交流,体现教师为主导、学生为主体的教学模式;
(2)通过空间向量在立体几何中的应用,提高学生的空间想象力,培养学生探索精神和创新意识,让学生感受数学,体会数学美的魅力,激发学生学数学、用数学的热情.
教学重难点
重点
难点
空间向量数量积公式及其应用.
(1)如何将立体几何问题等价转化为向量问题;
(2)在此基础上,通过向量运算解决立体几何问题.
知识要点
1.两个向量的夹角的定义
如图,已知两个非零向量a,b.在空间任取一点O,作OA=a,OB=b,则角∠AOB叫做向量a与b的夹角,记作:〈a,b〉
O
A
B
范围:0≤〈a,b〉≤π在这个规定下,两个向量的夹角就被唯一确定了,并且〈a,b〉= 〈b,a〉.
如果〈a,b〉= π/2,则称a与b互相垂直,并记作a⊥b .
2. 空间向量数量积的定义
设OA=a,则有向线段OA的长度叫做向量a的长度或模,记作: | a |
已知空间两个非零向量 , 则
叫做 的数量积,记作 , 即
(1)两个向量的数量积是数量,而不是向量.
(2)规定:零向量与任意向量的数量积等于零.
(3)
3.空间向量数量积的运算律
(交换律)
(分配律)
思考!
吗?
(2)对于向量 , 成立吗?
若m、n是平面α内的两条相交直线,且l⊥m, l⊥n. 则l ⊥α.
g
l
m
n
4.线面垂直的判定定理:
已知m,n是平面?内的两条相交直线,直线l与?的交点为B,且l⊥m,l⊥n,
求证:l⊥? .
例题1
n
m
g
g
m
n
?
l
l
分析:由定义可知,只需证l与平面内任意直线g垂直.
要证l与g垂直,只需证l·g=0
而m,n不平行,由共面向量定理知,存在唯一的有序实数对(x,y)使得 g=xm+yn
要证l·g=0,只需l· g= xl·m+yl·n=0
而l·m=0 ,l·n=0
故 l·g=0
在?内作不与m、n重合的任一条直线g,在l、m、n、g上取非零向量l、m、n、g,因m与n相交,得向量m、n不平行.
由共面向量定理可知,存在唯一的有序实数对(x,y),使
g=xm+yn, l·g=xl·m+yl·n
证明
∵ l·m=0, l·n=0
∴ l·g=0
∴ l⊥g
∴ l⊥g
这就证明了直线l垂直于平面?内的任一条直线,所以l⊥? .
继续
例题2
已知空间四边形ABCD的每条边和对角线的长都等于a,点M、N分别是边AB、CD的中点.
求证:MN⊥AB,MN⊥CD .
证明
因为
所以
同理,
已知:在空间四边形OABC中,OA⊥BC,OB⊥AC,求证:OC⊥AB.
例题3
A
B
C
O
继续
课堂小结
1.空间向量数量积的概念.
2.探究空间向量数量积运算的性质.
3.空间向量的运算律.
4.空间向量数量积的应用.
5. 通过学习,体会到我们可以利用向量数量积解决立体几何中的以下问题
(1)证明两直线垂直;
(2)求两点之间的距离或线段长度;
(3)证明线面垂直;
(4)求两直线所成角的余弦值等等.
(1)已知向量a,b满足| a |=1,| b |=2,|a - b|=3,则|a + b|=_________.
课堂练习
1.填空
1
方法一:发现|a + b|2+|a –b |2=2(| a |2+| b |2)带入求得.
有其他方法吗?
方法二:由|a –b|2=| a |2 - 2a·b + | b |2
带入求得a·b=-2.
∴|a + b|2=| a |2+2a·b+| b |2
得 |a+b|=1
方法三:数形结合法,发现形的特殊性.
继续
(2)已知 则a,b所成的夹角为_______.
分析:根据两向量夹角公式
可得到所求结果.
2.选择
设a,b,c是任意的非零空间向量,且相互不共线,则:
①(a·b)c-(c·a)b=0 ②|a|-|b|<|a-b|
③(b·c)a-(c·a)b不与c垂直
④(3a+2b)·(3a-2b)=9|a|2-4|b|2
中,真命题是( )
A. ①② B. ②③ C. ③④ D. ②④
D
3.解答题
如图,在平行六面体ABCD-A’B’C’D’ 中,E,F,G分别是A’D’,D’D,D’C’的中点,请选择恰当的基底向量证明:
①EG//AC
②平面EFG//平面AB’C
证明
取基底:
①
②
由①知
∴平面EFG//平面AB’C.
继续
