人教B版 选修2-1 高中数学 第三章 3.1.4空间向量的直角坐标运算 教学课件(共33张PPT)
文档属性
| 名称 | 人教B版 选修2-1 高中数学 第三章 3.1.4空间向量的直角坐标运算 教学课件(共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 782.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-08 20:43:26 | ||
图片预览








文档简介
(共33张PPT)
导入新课
复习平面向量基本定理
如果两向量a,b不共面,那么对平面任一向量p,均存在有序实数组{x,y},使得p=xa+yb.
当向量a垂直于向量b时,这种分解叫做平面向量的正交分解.
平面上向量的这些性质能推广到空间吗?
3.1.4空间向量的直角坐标运算
教学目标
知识目标
1. 了解空间向量基本定理及其意义;
2. 掌握空间向量的正交分解及其坐标表示;
3. 能够在简单问题中选用空间三个不共线向量作为基底表示其他向量.
能力目标
感受从特殊到一般的推导方式.
情感目标
承前启后,感悟数学与生活的和谐之美 ,体现数学的文化功能与人文价值.
教学重难点
重点
难点
空间向量的基本定理.
(1)空间向量的正交分解;
(2)空间向量的基本定理及其应用.
类比平面向量的正交分解,你能得出空间向量的正交分解吗?
探究
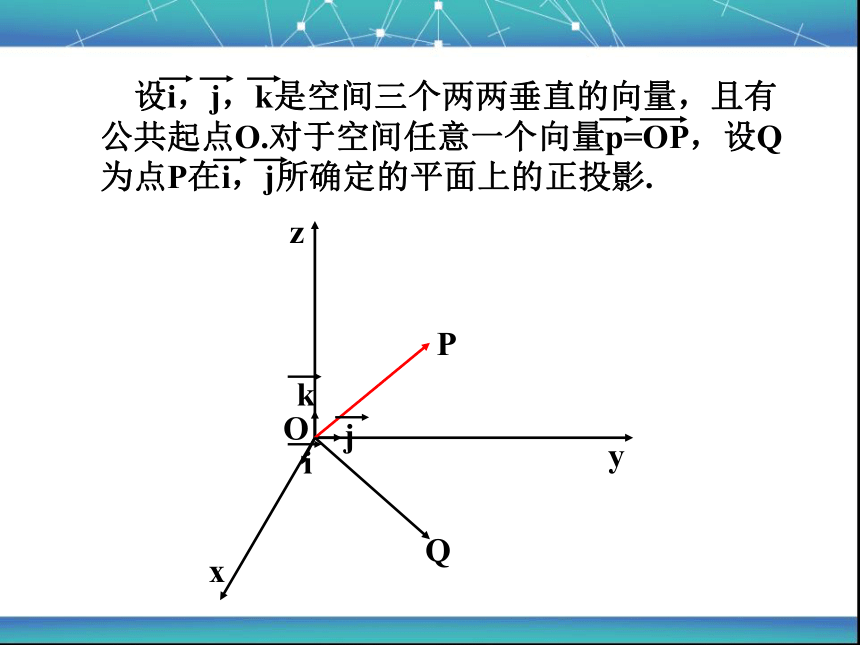
设i,j,k是空间三个两两垂直的向量,且有公共起点O.对于空间任意一个向量p=OP,设Q为点P在i,j所确定的平面上的正投影.
x
z
Q
P
i
j
k
O
y
x
z
Q
P
y
i
j
k
O
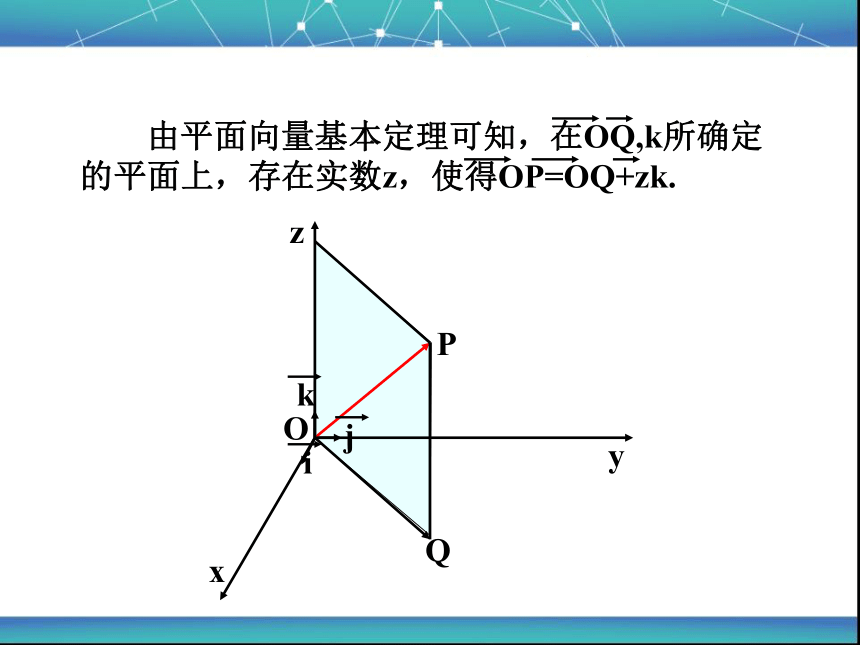
由平面向量基本定理可知,在OQ,k所确定的平面上,存在实数z,使得OP=OQ+zk.
x
z
Q
y
i
j
k
O
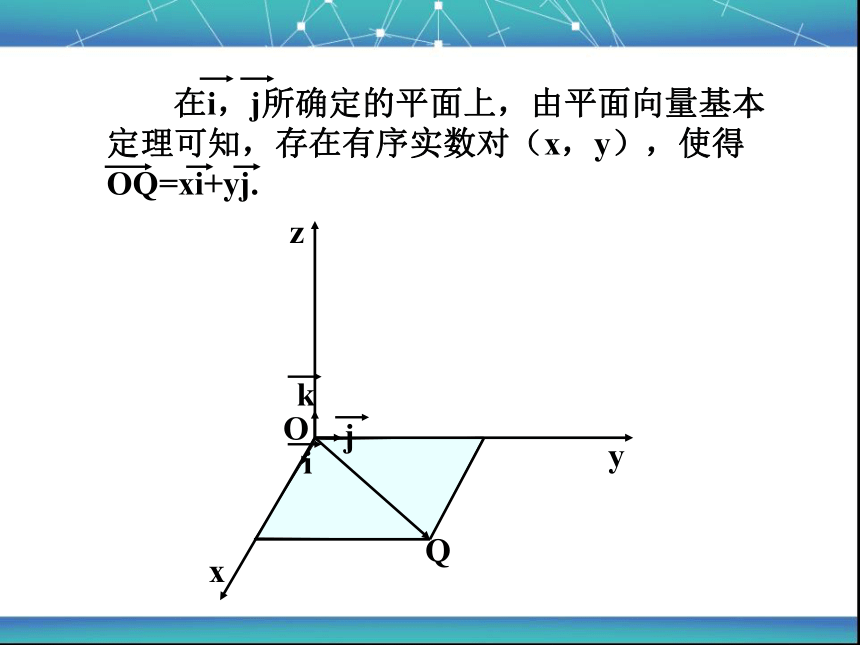
在i,j所确定的平面上,由平面向量基本定理可知,存在有序实数对(x,y),使得OQ=xi+yj.
x
z
Q
P
y
i
j
k
O
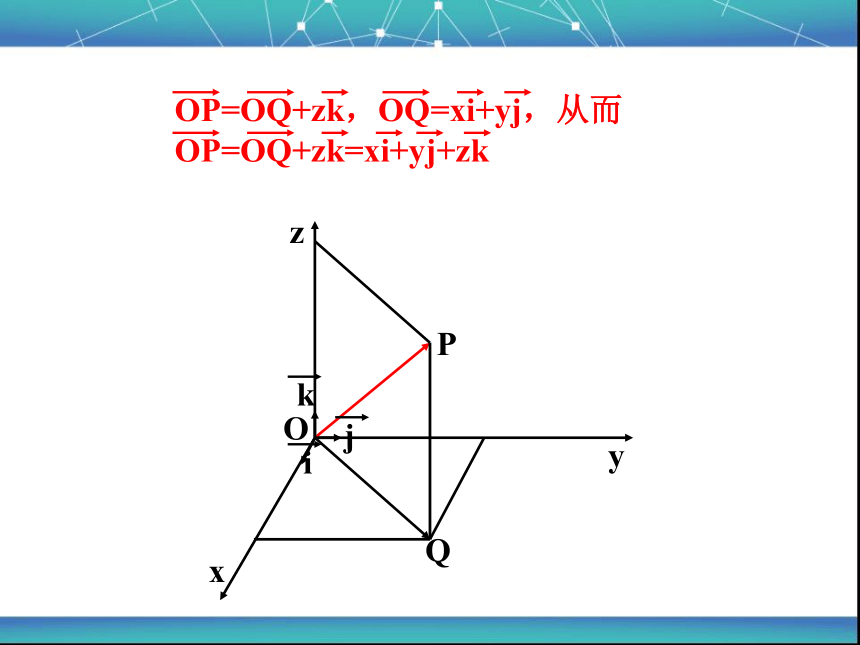
OP=OQ+zk,OQ=xi+yj,从而OP=OQ+zk=xi+yj+zk
空间向量的正交分解
空间向量的正交分解与平面向量的正交分解相似,区别在于分解的结果中多了“一项”.
注意
由上述证明可知,如果i,j,k是空间三个两两垂直的向量,那么,对空间任一向量p,存在一个有序实数组{x,y,z},使得p=xi+yj+zk.称xi,yj,zk为向量p在i,j,k上的分向量.
类比平面向量基本定理,你能得出空间向量基本定理吗?
探究
O
A
B
C
A'
B'
P'
P
设a,b,c不共面,过点O作OA=a,OB=b,OC=c,OP=p;过P作直线PP'平行于OC,交平面OAB与点P';在平面OAB中,过点P’作直线P'A'//OB,P'B'//OA.
O
A
B
C
A'
B'
P'
P
于是存在三个实数x,y,z,使
OA'=xOA=ya,OB'=yOB=yb,P'P=zOC=zc,
OP=OA'+OB'+P'P=xOA+yOB+zOC.
所以,p=xa+yb+zc.
空间向量基本定理
定理
如果三个向量a,b,c不共面,那么对空间任一向量p,存在有序实数组{x,y,z},使得
p=xa+yb+zc.
注意
空间向量基本定理说明,用空间三个不共面已知向量组{a,b,c}可以线性表示出空间任意一个向量,并且表达的结果是唯一的.
基底和基向量
由空间向量基本定理,如果三个向量a,b,c不共面,那么所有空间向量组成的集合就是{p|p=xa+yb+zc,x,y,z∈R}.
c
b
a
基向量
c
b
a
集合{p|p=xa+yb+zc,x,y,z∈R}可以看做是由向量a,b,c生成的.
{a,b,c}叫做空间的一个基底(base),a,b,c都叫做基向量(base vector).
注意
对于基底{a,b,c}需要明确以下几点:
1.向量a,b,c不共面;
2.空间任意三个不共面向量都可以做空间向量的一个基底;
3.由于0可视为与任意一个非零向量共线,与任意两个非零向量共面,所以三个向量不共面,就隐含着它们都不是0.
4.一个基底指一个向量组,一个基向量是指基底中的某一个向量.
设e1,e2,e3为有公共点O的三个两两垂直的单位向量(称它们为单位正交基底),以O为原点,分别以e1,e2,e3的方向为x轴,y轴,z轴的正方向建立空间直角坐标系Oxyz.
e1
e2
e3
x
y
z
O
e1
e2
e3
x
y
z
O
p
对于空间任意一个向量p,一定可以把它平移,使它的起点与原点O重合,得到向量OP=p.
P
这样,我们就有了从正交基底到空间直角坐标系的转换.
由空间向量基本定理可知,存在有序实数组{x,y,z},使得p=xe1+ye2+ze3.
把x,y,z称作向量p在单位正交基底e1,e2,e3下的坐标,记做p=(x,y,z).此时,向量p的坐标恰是点P在空间直角坐标系Oxyz中的坐标(x,y,z).
计算一下
计算单位正交基之间的数量积:e1?e2,e1?e3,e2?e3,e1?e1,e2?e2,e3?e3.
e1?e2=e1?e3=e2?e3=0.
e1?e1=e2?e2=e3?e3=1.
A
D
B
C
A1
B1
D1
E
F
C1
如图正方体ABCD-A'B'C'D',点E,F分别是上底面A'C'和侧面CD'的中心,若满足AF-AD=xAB+yAA',求x,y的值.?
例题
所以,
课堂小结
1.空间向量基本定理.
在空间,具有大小和方向的量如果三个向量a,b,c不共面,那么对空间任一向量p,存在有序实数组{x,y,z},使得p=xa+yb+zc.
2.基底与基向量.
空间任意三个不共面向量都可以做空间向量的一个基底.一个基底指一个向量组,一个基向量是指基底中的某一个向量.
3.空间向量的正交分解.
能从正交基底到空间直角坐标系转换.
课堂练习
1.已知空间四边形ABCD,连结AC,BD,设M,G分别是BC,CD的中点,则MG-AB+AD等于(???)
2.设e1,e2是平面上两个不共线向量,已知AB=2e1+ke2,CB=e1+3e2,CD=2e1-e2,若A,B,D三点共线,则k=_______________.
B
-8
A
B
C
O
M
N
Q
P
3.如下图,M,N分别为四面体OABC的边OA,BC的中点,P,Q是MN的三等分点.用向量OA,OB,OC表示OP和OQ.
A
B
C
O
M
N
Q
P
解答
A
B
C
O
M
N
Q
P
继续
导入新课
复习平面向量基本定理
如果两向量a,b不共面,那么对平面任一向量p,均存在有序实数组{x,y},使得p=xa+yb.
当向量a垂直于向量b时,这种分解叫做平面向量的正交分解.
平面上向量的这些性质能推广到空间吗?
3.1.4空间向量的直角坐标运算
教学目标
知识目标
1. 了解空间向量基本定理及其意义;
2. 掌握空间向量的正交分解及其坐标表示;
3. 能够在简单问题中选用空间三个不共线向量作为基底表示其他向量.
能力目标
感受从特殊到一般的推导方式.
情感目标
承前启后,感悟数学与生活的和谐之美 ,体现数学的文化功能与人文价值.
教学重难点
重点
难点
空间向量的基本定理.
(1)空间向量的正交分解;
(2)空间向量的基本定理及其应用.
类比平面向量的正交分解,你能得出空间向量的正交分解吗?
探究
设i,j,k是空间三个两两垂直的向量,且有公共起点O.对于空间任意一个向量p=OP,设Q为点P在i,j所确定的平面上的正投影.
x
z
Q
P
i
j
k
O
y
x
z
Q
P
y
i
j
k
O
由平面向量基本定理可知,在OQ,k所确定的平面上,存在实数z,使得OP=OQ+zk.
x
z
Q
y
i
j
k
O
在i,j所确定的平面上,由平面向量基本定理可知,存在有序实数对(x,y),使得OQ=xi+yj.
x
z
Q
P
y
i
j
k
O
OP=OQ+zk,OQ=xi+yj,从而OP=OQ+zk=xi+yj+zk
空间向量的正交分解
空间向量的正交分解与平面向量的正交分解相似,区别在于分解的结果中多了“一项”.
注意
由上述证明可知,如果i,j,k是空间三个两两垂直的向量,那么,对空间任一向量p,存在一个有序实数组{x,y,z},使得p=xi+yj+zk.称xi,yj,zk为向量p在i,j,k上的分向量.
类比平面向量基本定理,你能得出空间向量基本定理吗?
探究
O
A
B
C
A'
B'
P'
P
设a,b,c不共面,过点O作OA=a,OB=b,OC=c,OP=p;过P作直线PP'平行于OC,交平面OAB与点P';在平面OAB中,过点P’作直线P'A'//OB,P'B'//OA.
O
A
B
C
A'
B'
P'
P
于是存在三个实数x,y,z,使
OA'=xOA=ya,OB'=yOB=yb,P'P=zOC=zc,
OP=OA'+OB'+P'P=xOA+yOB+zOC.
所以,p=xa+yb+zc.
空间向量基本定理
定理
如果三个向量a,b,c不共面,那么对空间任一向量p,存在有序实数组{x,y,z},使得
p=xa+yb+zc.
注意
空间向量基本定理说明,用空间三个不共面已知向量组{a,b,c}可以线性表示出空间任意一个向量,并且表达的结果是唯一的.
基底和基向量
由空间向量基本定理,如果三个向量a,b,c不共面,那么所有空间向量组成的集合就是{p|p=xa+yb+zc,x,y,z∈R}.
c
b
a
基向量
c
b
a
集合{p|p=xa+yb+zc,x,y,z∈R}可以看做是由向量a,b,c生成的.
{a,b,c}叫做空间的一个基底(base),a,b,c都叫做基向量(base vector).
注意
对于基底{a,b,c}需要明确以下几点:
1.向量a,b,c不共面;
2.空间任意三个不共面向量都可以做空间向量的一个基底;
3.由于0可视为与任意一个非零向量共线,与任意两个非零向量共面,所以三个向量不共面,就隐含着它们都不是0.
4.一个基底指一个向量组,一个基向量是指基底中的某一个向量.
设e1,e2,e3为有公共点O的三个两两垂直的单位向量(称它们为单位正交基底),以O为原点,分别以e1,e2,e3的方向为x轴,y轴,z轴的正方向建立空间直角坐标系Oxyz.
e1
e2
e3
x
y
z
O
e1
e2
e3
x
y
z
O
p
对于空间任意一个向量p,一定可以把它平移,使它的起点与原点O重合,得到向量OP=p.
P
这样,我们就有了从正交基底到空间直角坐标系的转换.
由空间向量基本定理可知,存在有序实数组{x,y,z},使得p=xe1+ye2+ze3.
把x,y,z称作向量p在单位正交基底e1,e2,e3下的坐标,记做p=(x,y,z).此时,向量p的坐标恰是点P在空间直角坐标系Oxyz中的坐标(x,y,z).
计算一下
计算单位正交基之间的数量积:e1?e2,e1?e3,e2?e3,e1?e1,e2?e2,e3?e3.
e1?e2=e1?e3=e2?e3=0.
e1?e1=e2?e2=e3?e3=1.
A
D
B
C
A1
B1
D1
E
F
C1
如图正方体ABCD-A'B'C'D',点E,F分别是上底面A'C'和侧面CD'的中心,若满足AF-AD=xAB+yAA',求x,y的值.?
例题
所以,
课堂小结
1.空间向量基本定理.
在空间,具有大小和方向的量如果三个向量a,b,c不共面,那么对空间任一向量p,存在有序实数组{x,y,z},使得p=xa+yb+zc.
2.基底与基向量.
空间任意三个不共面向量都可以做空间向量的一个基底.一个基底指一个向量组,一个基向量是指基底中的某一个向量.
3.空间向量的正交分解.
能从正交基底到空间直角坐标系转换.
课堂练习
1.已知空间四边形ABCD,连结AC,BD,设M,G分别是BC,CD的中点,则MG-AB+AD等于(???)
2.设e1,e2是平面上两个不共线向量,已知AB=2e1+ke2,CB=e1+3e2,CD=2e1-e2,若A,B,D三点共线,则k=_______________.
B
-8
A
B
C
O
M
N
Q
P
3.如下图,M,N分别为四面体OABC的边OA,BC的中点,P,Q是MN的三等分点.用向量OA,OB,OC表示OP和OQ.
A
B
C
O
M
N
Q
P
解答
A
B
C
O
M
N
Q
P
继续
