人教B版 选修2-1 高中数学 第三章 3.2.3直线与平面的夹角 教学课件(共27张PPT)
文档属性
| 名称 | 人教B版 选修2-1 高中数学 第三章 3.2.3直线与平面的夹角 教学课件(共27张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 890.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-08 00:00:00 | ||
图片预览






文档简介
(共27张PPT)
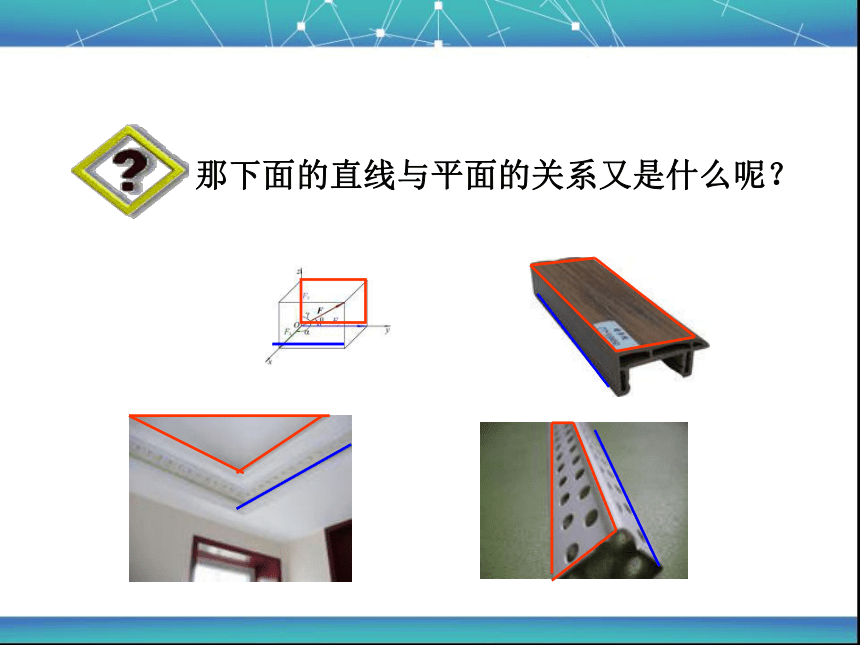
下面的直线与平面有什么关系?
新课导入
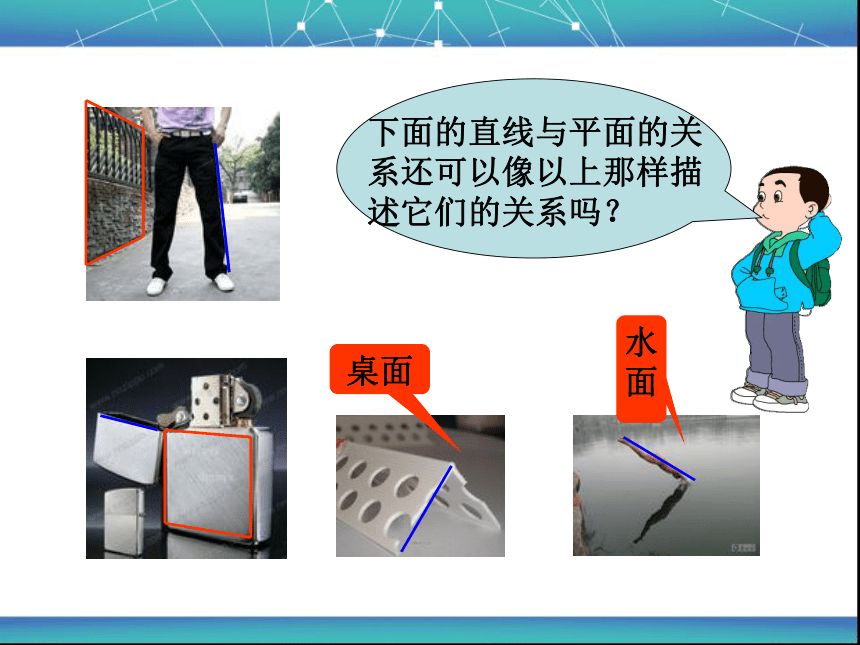
那下面的直线与平面的关系又是什么呢?
下面的直线与平面的关系还可以像以上那样描述它们的关系吗?
桌面
水面
3.2.3 直线与平面的夹角
教学目标
知识与能力
知道斜线与平面的夹角含义,体会夹角定义的唯一性与合理性。
过程与方法
理解并会推导cosθ= cosθ1 cosθ2的证明过程。
情感态度与价值观
培养同学们观察生活并从中提出问题的能力以及利用数学解决实际问题的能力。
教学重难点
重点
难点
直线与平面的夹角的定义理解
公式推导过程的应用
研讨
α
θ
θ2
θ1
A
B
O
m
M
看下图:
α
θ
θ2
θ1
A
B
O
m
M
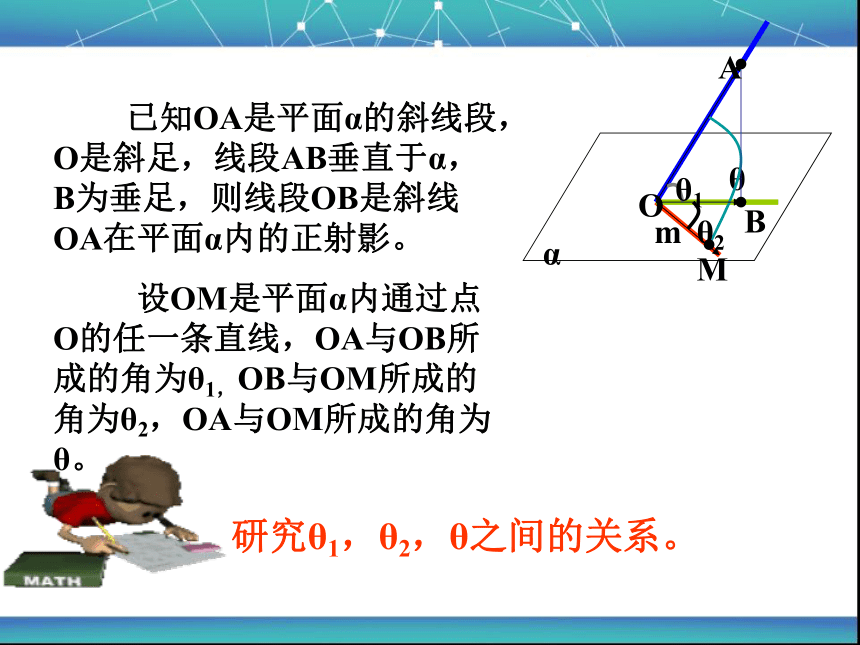
已知OA是平面α的斜线段,O是斜足,线段AB垂直于α,B为垂足,则线段OB是斜线OA在平面α内的正射影。
设OM是平面α内通过点O的任一条直线,OA与OB所成的角为θ1,OB与OM所成的角为θ2,OA与OM所成的角为θ。
研究θ1,θ2,θ之间的关系。
很重要!
α
θ
θ2
θ1
A
B
O
m
M
过程
在直线OM上取单位向量 ,
则 ,即
。
因为
所以
α
θ
θ2
θ1
A
B
O
m
M
因此
即
又
α
θ
θ2
θ1
A
B
O
m
M
所以
知识要点
推导过程很重要喔!
小总结
此公式在以后的学习过程中非常的重要,
记住此公式可以省去很多的思考过程,节省
做题时间,加快做题的速度,其推导的过程
也是不可以忽视的,在很多大的证明题和解
答题中需要用到喔!
探后余思
此公式的推导过程运用了什么方法?_________
三垂线法
此公式还可以用其他方法证明吗?_________
向量法
(请自己完成证明过程)
1
2
θ与θ1的大小如何呢?
因为0≤ cos θ2≤1,所以cos θ≤ cos θ1
因为角都为锐角或者直角,所以 θ1<θ
由此得到
斜线和它在平面内的射影所成的角,是斜线和
这个平面内所有直线所成角中最小的角。
斜线和它在平面内的射影所成的角叫做斜线
和平面所成的角。
规定
斜线和平面所成的角
α
θ
A
B
重点掌握喔
思考…
斜线和平面的夹角的范围???
斜线与平面所成的夹角为锐角(不包括法线与平行线)。
结论
夹角是唯一的,指的是与该平面内所有直线所成角的最小角。
体会
试证明
A1
B1
A
B
α
A1为A在平面内的射影
B1为B在平面内的射影
斜线AB与平面的夹角为θ
证明:
(自己完成)
小练习
例1 设直线L:(x-1)/2=y/(-1)=(z+1)/2,平面x-y+2z+3,求直线与平面的夹角.
解
为所求夹角.
又与直线
相交的直线方程.
例2 求过点 M (-1,2,-3), 且平行于平面
P
M
L
P1
M1
分析: 关键是求得直线上另外一个点 M1. M1在过M且平行于 平面 P 的一个平面P1上,待求直线又与已知直线相交,交点既在P1上,又在 L上,因此是L与P1的交点.
P
M
L
P1
M1
解 过M作平行于 平面 P 的一个点P1
求平面 P1与已知直线 L的交点
P1:
即P1:
解得,
课堂小结
1.角之间的关系
α
θ
θ2
θ1
A
B
O
m
M
2.直线与平面的夹角的定义
斜线和它在平面内的射影所成的角叫做斜线和平面所成的角。
α
θ
A
B
3.直线与平面的夹角的求法
A1
B1
A
B
α
下面的直线与平面有什么关系?
新课导入
那下面的直线与平面的关系又是什么呢?
下面的直线与平面的关系还可以像以上那样描述它们的关系吗?
桌面
水面
3.2.3 直线与平面的夹角
教学目标
知识与能力
知道斜线与平面的夹角含义,体会夹角定义的唯一性与合理性。
过程与方法
理解并会推导cosθ= cosθ1 cosθ2的证明过程。
情感态度与价值观
培养同学们观察生活并从中提出问题的能力以及利用数学解决实际问题的能力。
教学重难点
重点
难点
直线与平面的夹角的定义理解
公式推导过程的应用
研讨
α
θ
θ2
θ1
A
B
O
m
M
看下图:
α
θ
θ2
θ1
A
B
O
m
M
已知OA是平面α的斜线段,O是斜足,线段AB垂直于α,B为垂足,则线段OB是斜线OA在平面α内的正射影。
设OM是平面α内通过点O的任一条直线,OA与OB所成的角为θ1,OB与OM所成的角为θ2,OA与OM所成的角为θ。
研究θ1,θ2,θ之间的关系。
很重要!
α
θ
θ2
θ1
A
B
O
m
M
过程
在直线OM上取单位向量 ,
则 ,即
。
因为
所以
α
θ
θ2
θ1
A
B
O
m
M
因此
即
又
α
θ
θ2
θ1
A
B
O
m
M
所以
知识要点
推导过程很重要喔!
小总结
此公式在以后的学习过程中非常的重要,
记住此公式可以省去很多的思考过程,节省
做题时间,加快做题的速度,其推导的过程
也是不可以忽视的,在很多大的证明题和解
答题中需要用到喔!
探后余思
此公式的推导过程运用了什么方法?_________
三垂线法
此公式还可以用其他方法证明吗?_________
向量法
(请自己完成证明过程)
1
2
θ与θ1的大小如何呢?
因为0≤ cos θ2≤1,所以cos θ≤ cos θ1
因为角都为锐角或者直角,所以 θ1<θ
由此得到
斜线和它在平面内的射影所成的角,是斜线和
这个平面内所有直线所成角中最小的角。
斜线和它在平面内的射影所成的角叫做斜线
和平面所成的角。
规定
斜线和平面所成的角
α
θ
A
B
重点掌握喔
思考…
斜线和平面的夹角的范围???
斜线与平面所成的夹角为锐角(不包括法线与平行线)。
结论
夹角是唯一的,指的是与该平面内所有直线所成角的最小角。
体会
试证明
A1
B1
A
B
α
A1为A在平面内的射影
B1为B在平面内的射影
斜线AB与平面的夹角为θ
证明:
(自己完成)
小练习
例1 设直线L:(x-1)/2=y/(-1)=(z+1)/2,平面x-y+2z+3,求直线与平面的夹角.
解
为所求夹角.
又与直线
相交的直线方程.
例2 求过点 M (-1,2,-3), 且平行于平面
P
M
L
P1
M1
分析: 关键是求得直线上另外一个点 M1. M1在过M且平行于 平面 P 的一个平面P1上,待求直线又与已知直线相交,交点既在P1上,又在 L上,因此是L与P1的交点.
P
M
L
P1
M1
解 过M作平行于 平面 P 的一个点P1
求平面 P1与已知直线 L的交点
P1:
即P1:
解得,
课堂小结
1.角之间的关系
α
θ
θ2
θ1
A
B
O
m
M
2.直线与平面的夹角的定义
斜线和它在平面内的射影所成的角叫做斜线和平面所成的角。
α
θ
A
B
3.直线与平面的夹角的求法
A1
B1
A
B
α
