人教B版 选修2-1 高中数学 第三章 3.2.5距离(选学)教学课件(共32张PPT)
文档属性
| 名称 | 人教B版 选修2-1 高中数学 第三章 3.2.5距离(选学)教学课件(共32张PPT) | 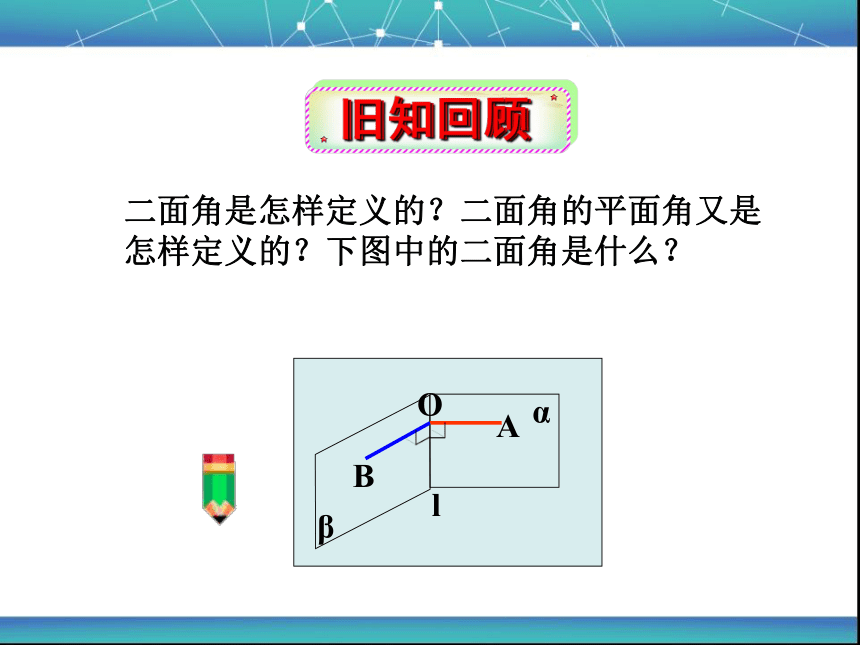 | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-08 20:42:51 | ||
图片预览







文档简介
(共32张PPT)
α
β
l
二面角是怎样定义的?二面角的平面角又是怎样定义的?下图中的二面角是什么?
O
A
B
旧知回顾
旧知回顾
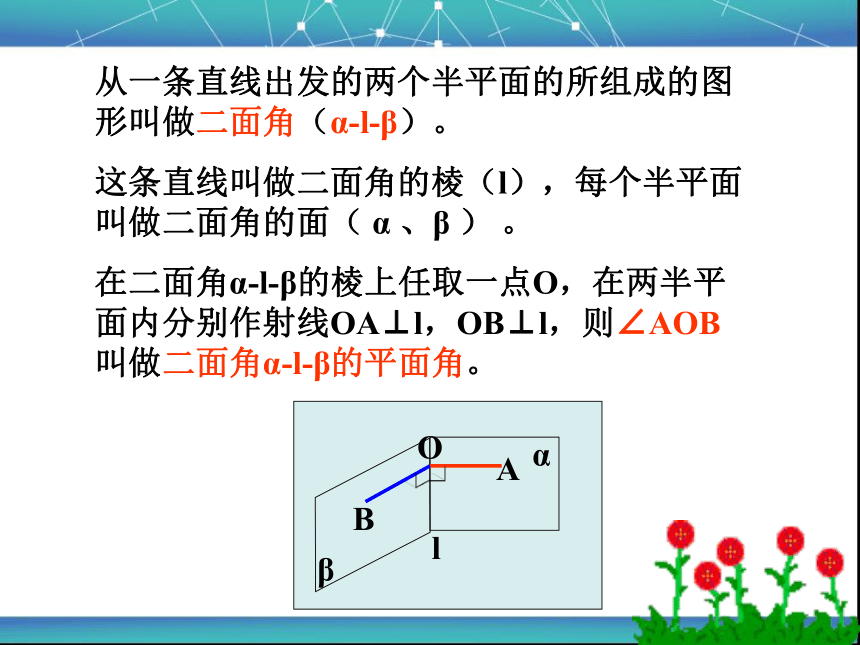
从一条直线出发的两个半平面的所组成的图形叫做二面角(α-l-β)。
这条直线叫做二面角的棱(l),每个半平面叫做二面角的面( α 、β ) 。
在二面角α-l-β的棱上任取一点O,在两半平面内分别作射线OA⊥l,OB⊥l,则∠AOB叫做二面角α-l-β的平面角。
α
β
l
O
A
B
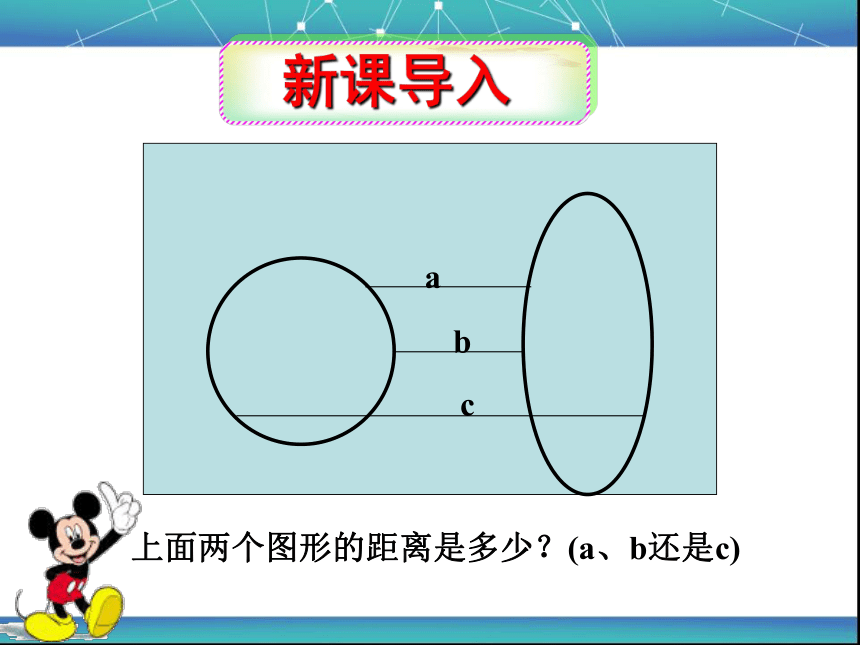
新课导入
上面两个图形的距离是多少?(a、b还是c)
a
b
c
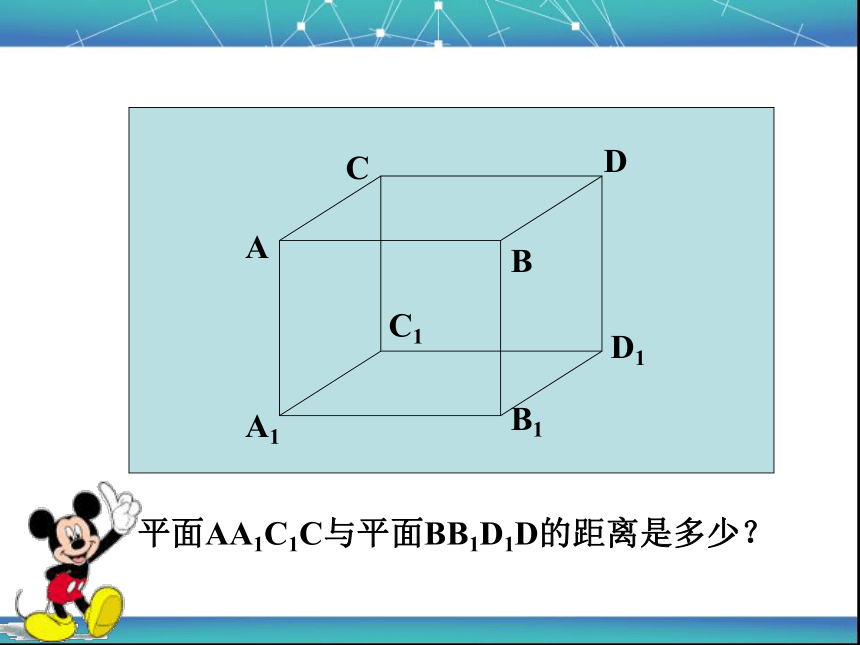
A
A1
B
C
D
C1
D1
B1
平面AA1C1C与平面BB1D1D的距离是多少?
α
P
点P与平面α的距离是多少?
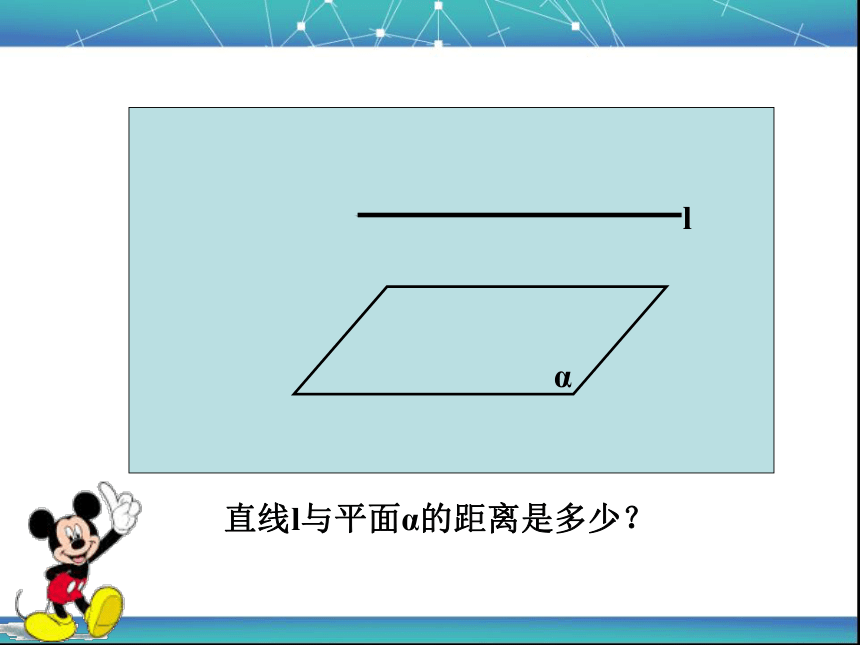
α
l
直线l与平面α的距离是多少?
3.2.5 距离(选学)
教学目标
能理解图形与图形距离的概念
知道点到平面的距离、直线与它的平行平面的距离、两个平行平面的距离的概念并会求它的距离。
知识与能力
会用向量勾股定理、三角函数等方法求距离。
培养学生知识迁移、知识整合的能力。
过程与方法
情感态度与价值观
教学重难点
重点
难点
理解距离的概念
距离的求法
知识要点
一个图形内的任一点与另一个图形内的
任一点的距离中的最小值,叫做图形与
图形的距离。
距离的概念
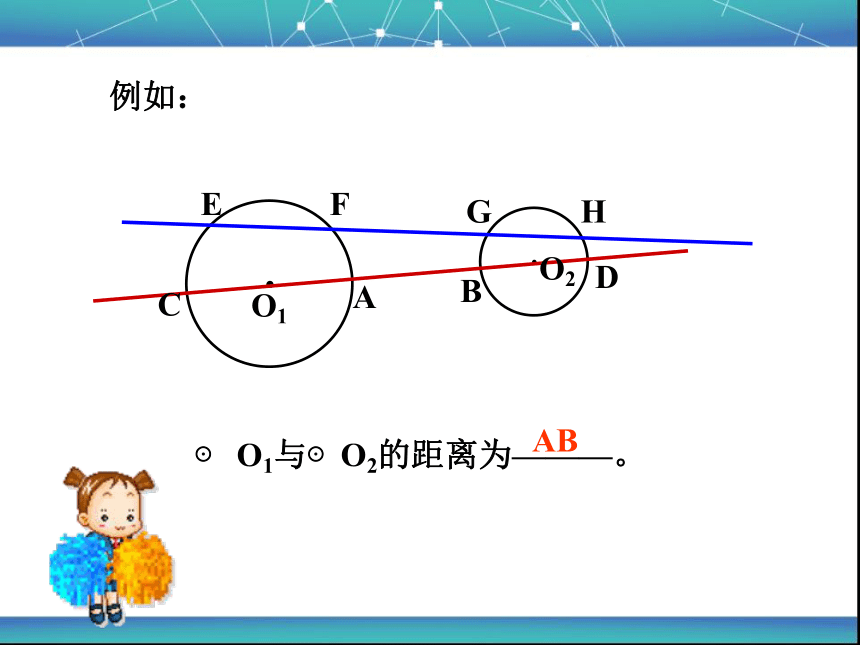
例如:
A
B
O1
O2
C
D
E
F
G
H
⊙ O1与⊙O2的距离为———。
AB
点到平面的距离
连接平面α外一点P与α内任意一点的所有
线段中,垂线段最短。
一点到它在一个平面内正射影的距离,叫
做点到这个平面的距离。
例如:
α
P
O
A
B
点P与平面α的距离为————
PO
直线与它的平行平面的距离
如果一条直线平行于平面α,则直线上的各点到平面所作的垂线段相等,即各点到α的距离相等。
一条直线上的任一点,与它平行的平面的距离,叫做直线与这个平面的距离。
例如:
α
平行于平面α的直线l与α的距离为————
l
O1
M
O2
N
MO1、NO2
P
O3
两个平行平面的距离
和两个平行平面同时垂直的直线,叫做两个平面的公垂线。
公垂线加在平行平面间的部分,叫做两个平行平面的公垂线段。
两平行平面的共垂线段的长度,叫做两平行平面的距离。
例如:
α
β
A
B
A1
B2
AA1、BB2叫做两个平面的————,
即两平行平面的————。
公垂线段
距离
距离的度量
计算图形之间的距离,一般我们可以
采用勾股定理、三角函数和向量的内
积运算。
计算任何图形之间的距离都可以转化为求两点之间的距离。
注意
两点之间的距离的求法可以采用向量法。
例如:
已知正方体ABCD-A1B1C1D1的棱长为1,点P为AD1的中点,Q是BD上一点,DQ=1/4BD,求P、Q之间的距离。
解:以向量 所在的
直线为x轴、y轴和z轴建立空
间直角坐标系D-xyz,则
P(1/2,0,1/2)、Q(1/4,1/4,0),
所以 =(-1/4,1/4,-1/2)
故 = ,即P、Q两点的距离是 。
例题
在长方体OABC-O1A1B1C1中,OA=2,
AB=3,AA1=2,求点O1到直线AC的距
离。
解:建立如图所示空间直角
坐标系,连结AO1,AC,则
A(2,0,0),B(0,3,0),O1(0,0,2)。
所以
故
课堂小结
一个图形内的任一点与另一个图形
内的任一点的距离中的最小值,叫
做图形与图形的距离。
2. 一点到它在一个平面内正射影的距离,叫
做点到这个平面的距离。
3.一条直线上的任一点,与它平行的平
面的距离,叫做直线与这个平面的距
离。
4.两平行平面的共垂线段的长度,叫做
两平行平面的距离。
5.计算图形之间的距离,一般我们可以
采用勾股定理、三角函数和向量的内
积运算。
课堂练习
在三棱锥P-ABC中,三角形ABC是边长为
6的等边三角形,PA=PB=PC= ,则点
P到平面ABC的距离是——;
若P、A、B、C四
点在某个球面上,
则球的半径为——。
6
4
在120度的二面角α-l-β内有一点P,P
在平面α、β内的射影A、B分别落在
平面α、β内,且PA=3,PB=4,则P
到l的距离为————。
答案:
已知ABCD是边长为4的正方形,E、
F分别是AB、CD的中点,GC垂直于
ABCD所在的平面,且GC=2,求点
B到平面EFG的距离。
答案:
已知E、F、G、H分别是空间四边形
ABCD四条边AB、BC、CD、DA的
中点,且AC=2,BD=4,则EG2+FH2
=————。
答案:10
设P、Q是单位正方体AC1的面AA1DD1
、面A1B1C1D1的中心。如图,
(1)证明:PQ∥平面AA1BB1;
(2)求线段PQ的长。
A
B
C
D
D1
C1
A1
B1
P
Q
答案:
(1)证明:连结AD1,AB1,
在三角形AB1D1中,显然P、
Q分别是AD1、D1B的中点,
所以PQ ∥AB,且PQ=1/2AB1
因为PQ不包含于面AA1B1B,AB1包含于面AA1B1B
所以PQ ∥面AA1B1B
(2)PQ=1/2AB1=
A
B
C
D
D1
C1
A1
B1
P
Q
α
β
l
二面角是怎样定义的?二面角的平面角又是怎样定义的?下图中的二面角是什么?
O
A
B
旧知回顾
旧知回顾
从一条直线出发的两个半平面的所组成的图形叫做二面角(α-l-β)。
这条直线叫做二面角的棱(l),每个半平面叫做二面角的面( α 、β ) 。
在二面角α-l-β的棱上任取一点O,在两半平面内分别作射线OA⊥l,OB⊥l,则∠AOB叫做二面角α-l-β的平面角。
α
β
l
O
A
B
新课导入
上面两个图形的距离是多少?(a、b还是c)
a
b
c
A
A1
B
C
D
C1
D1
B1
平面AA1C1C与平面BB1D1D的距离是多少?
α
P
点P与平面α的距离是多少?
α
l
直线l与平面α的距离是多少?
3.2.5 距离(选学)
教学目标
能理解图形与图形距离的概念
知道点到平面的距离、直线与它的平行平面的距离、两个平行平面的距离的概念并会求它的距离。
知识与能力
会用向量勾股定理、三角函数等方法求距离。
培养学生知识迁移、知识整合的能力。
过程与方法
情感态度与价值观
教学重难点
重点
难点
理解距离的概念
距离的求法
知识要点
一个图形内的任一点与另一个图形内的
任一点的距离中的最小值,叫做图形与
图形的距离。
距离的概念
例如:
A
B
O1
O2
C
D
E
F
G
H
⊙ O1与⊙O2的距离为———。
AB
点到平面的距离
连接平面α外一点P与α内任意一点的所有
线段中,垂线段最短。
一点到它在一个平面内正射影的距离,叫
做点到这个平面的距离。
例如:
α
P
O
A
B
点P与平面α的距离为————
PO
直线与它的平行平面的距离
如果一条直线平行于平面α,则直线上的各点到平面所作的垂线段相等,即各点到α的距离相等。
一条直线上的任一点,与它平行的平面的距离,叫做直线与这个平面的距离。
例如:
α
平行于平面α的直线l与α的距离为————
l
O1
M
O2
N
MO1、NO2
P
O3
两个平行平面的距离
和两个平行平面同时垂直的直线,叫做两个平面的公垂线。
公垂线加在平行平面间的部分,叫做两个平行平面的公垂线段。
两平行平面的共垂线段的长度,叫做两平行平面的距离。
例如:
α
β
A
B
A1
B2
AA1、BB2叫做两个平面的————,
即两平行平面的————。
公垂线段
距离
距离的度量
计算图形之间的距离,一般我们可以
采用勾股定理、三角函数和向量的内
积运算。
计算任何图形之间的距离都可以转化为求两点之间的距离。
注意
两点之间的距离的求法可以采用向量法。
例如:
已知正方体ABCD-A1B1C1D1的棱长为1,点P为AD1的中点,Q是BD上一点,DQ=1/4BD,求P、Q之间的距离。
解:以向量 所在的
直线为x轴、y轴和z轴建立空
间直角坐标系D-xyz,则
P(1/2,0,1/2)、Q(1/4,1/4,0),
所以 =(-1/4,1/4,-1/2)
故 = ,即P、Q两点的距离是 。
例题
在长方体OABC-O1A1B1C1中,OA=2,
AB=3,AA1=2,求点O1到直线AC的距
离。
解:建立如图所示空间直角
坐标系,连结AO1,AC,则
A(2,0,0),B(0,3,0),O1(0,0,2)。
所以
故
课堂小结
一个图形内的任一点与另一个图形
内的任一点的距离中的最小值,叫
做图形与图形的距离。
2. 一点到它在一个平面内正射影的距离,叫
做点到这个平面的距离。
3.一条直线上的任一点,与它平行的平
面的距离,叫做直线与这个平面的距
离。
4.两平行平面的共垂线段的长度,叫做
两平行平面的距离。
5.计算图形之间的距离,一般我们可以
采用勾股定理、三角函数和向量的内
积运算。
课堂练习
在三棱锥P-ABC中,三角形ABC是边长为
6的等边三角形,PA=PB=PC= ,则点
P到平面ABC的距离是——;
若P、A、B、C四
点在某个球面上,
则球的半径为——。
6
4
在120度的二面角α-l-β内有一点P,P
在平面α、β内的射影A、B分别落在
平面α、β内,且PA=3,PB=4,则P
到l的距离为————。
答案:
已知ABCD是边长为4的正方形,E、
F分别是AB、CD的中点,GC垂直于
ABCD所在的平面,且GC=2,求点
B到平面EFG的距离。
答案:
已知E、F、G、H分别是空间四边形
ABCD四条边AB、BC、CD、DA的
中点,且AC=2,BD=4,则EG2+FH2
=————。
答案:10
设P、Q是单位正方体AC1的面AA1DD1
、面A1B1C1D1的中心。如图,
(1)证明:PQ∥平面AA1BB1;
(2)求线段PQ的长。
A
B
C
D
D1
C1
A1
B1
P
Q
答案:
(1)证明:连结AD1,AB1,
在三角形AB1D1中,显然P、
Q分别是AD1、D1B的中点,
所以PQ ∥AB,且PQ=1/2AB1
因为PQ不包含于面AA1B1B,AB1包含于面AA1B1B
所以PQ ∥面AA1B1B
(2)PQ=1/2AB1=
A
B
C
D
D1
C1
A1
B1
P
Q
