人教版高中数学必修二第二章2.2.1 直线和平面平行的判定课件(共15张PPT)
文档属性
| 名称 | 人教版高中数学必修二第二章2.2.1 直线和平面平行的判定课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 793.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-08 20:49:13 | ||
图片预览




文档简介
(共15张PPT)
2.2.1 直线和平面平行的判定
1.空间直线与平面的位置关系有哪几种?
直线 与平面?平行
直线 与平面?相交
?
?
?
?
∩?=A
// ?
直线 在平面?内
?
A
一、复习引入:直线与平面的位置关系
无数个公共点
0个公共点
一个公共点
球场地面
感受校园生活中线面平行的例子
二、实例探究
电棒所在的直线与天花板所在的平面
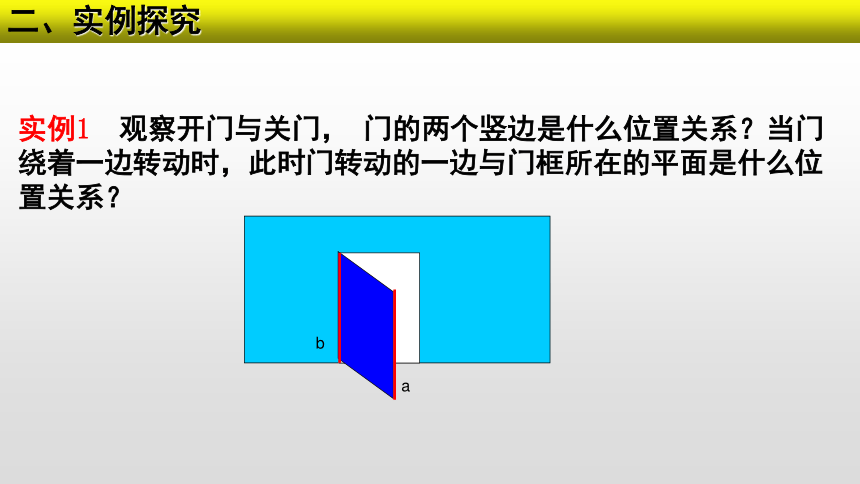
实例1 观察开门与关门, 门的两个竖边是什么位置关系?当门绕着一边转动时,此时门转动的一边与门框所在的平面是什么位置关系?
二、实例探究
a
b
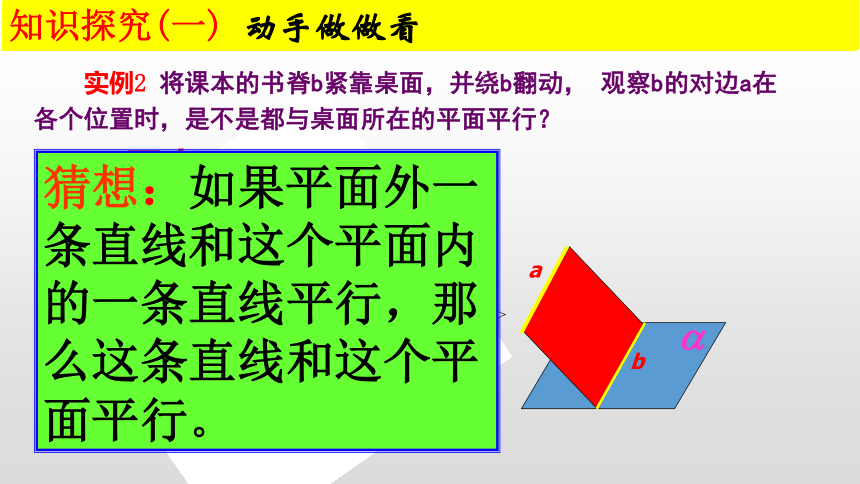
实例2 将课本的书脊b紧靠桌面,并绕b翻动, 观察b的对边a在各个位置时,是不是都与桌面所在的平面平行?
转化平面
知识探究(二) 直线与平面平行的判定
a
a
b
1 直线a和b共面吗?
2 a与平面?相交吗?
3 由上你能猜想出判定线面平行的关键所在吗?
思考:
猜想:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
?
知识探究(一) 动手做做看
a
b
α
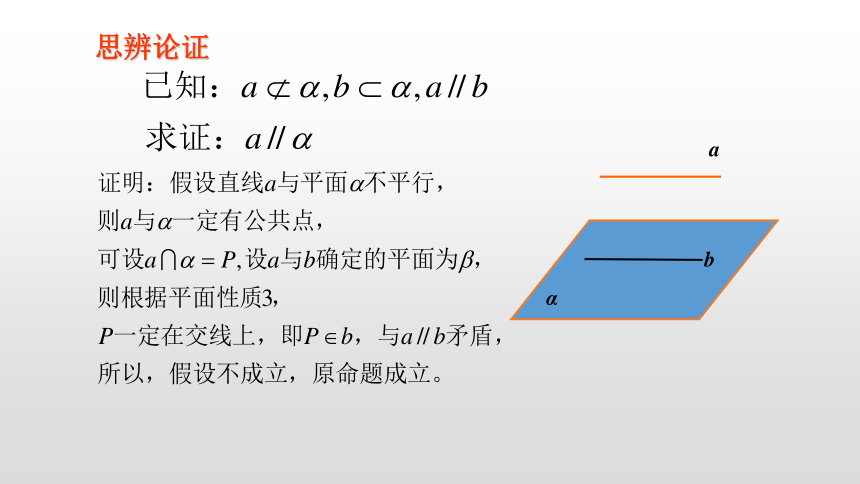
思辨论证
平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行 。
b??
a∥ b
a ??
a ∥ ?
注明:
1、定理三个条件缺一不可。
2、简记:线线平行,则线面平行。
3、定理告诉我们:
要证线面平行,得在面内找一条线,使线线平行。
b
符号语言
三、抽象概括
直线与平面平行的判定定理:
已知:空间四边形ABCD中,E,F分别是AB,DA的中点。
求证:EF//平面BCD
例1 求证:空间四边形相邻两边中点的连线平行于经过另外两边所在的平面
符号语言:
C
D
B
E
F
A
四、定理应用
A
B
C
D
E
F
例1 求证:空间四边形相邻两边中点的连线平行于经过另外两边所在的平面.
已知:空间四边形ABCD中,E,F分别AB,AD的中点.
求证:EF//平面BCD.
证明:连接BD.
因为 AE=EB , AF=FD,
所以 EF//BD(三角形中位线的性质)
因为
由直线与平面平行的判断定理得
EF//平面BCD.
规范答题参考
1.如图,在空间四边形ABCD中,E、F分
别为AB、AD上的点,若 , 则EF
与平面BCD的位置关系是 ____________.
EF//平面BCD
变式训练:
A
B
C
D
E
F
练习1:如图,长方体 中,
①与 平行的平面是 ____________________________
②与 平行的平面是____________________________
③与 平行的平面是________________________
五、学以致用
分析:要证BD1//平面AEC,
即要在平面AEC内找一条直线与BD1平行.
练习2. 如图,正方体ABCD-A1B1C1D1中,E为DD1的中点.
求证: BD1∥平面AEC
F
E
D1
B1
A1
D
B
A
C1
C
证明:
∴EF∥BD1.
∴ BD1 ∥平面AEC.
是DD1 、BD的中点.
∵ 在△ BDD1中,E、F分别
连接BD,交AC于F点,再连接EF.
EF 平面AEC,
∩
∵ BD1 平面AEC,
五、学以致用
1、直线与平面平行判定定理:
线(面外)线(面内)平行?线面平行
2、运用定理的关键找平行线。找平行线又经常会用到三角形中位线、梯形的中位线、平行四边形、平行公理。(一般题中有中点再找中点,有分点再找分点得平行关系.)
“一线面内、一线面外、两线平行”
3、数学思想方法:
转化与化归的思想
将线面平行转化为线线平行
将空间问题转化为平面问题
课时小结:
六、课时小结
作业:
1、导学案:能力提升
2、课本P62 3
谢谢
再见
2.2.1 直线和平面平行的判定
1.空间直线与平面的位置关系有哪几种?
直线 与平面?平行
直线 与平面?相交
?
?
?
?
∩?=A
// ?
直线 在平面?内
?
A
一、复习引入:直线与平面的位置关系
无数个公共点
0个公共点
一个公共点
球场地面
感受校园生活中线面平行的例子
二、实例探究
电棒所在的直线与天花板所在的平面
实例1 观察开门与关门, 门的两个竖边是什么位置关系?当门绕着一边转动时,此时门转动的一边与门框所在的平面是什么位置关系?
二、实例探究
a
b
实例2 将课本的书脊b紧靠桌面,并绕b翻动, 观察b的对边a在各个位置时,是不是都与桌面所在的平面平行?
转化平面
知识探究(二) 直线与平面平行的判定
a
a
b
1 直线a和b共面吗?
2 a与平面?相交吗?
3 由上你能猜想出判定线面平行的关键所在吗?
思考:
猜想:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
?
知识探究(一) 动手做做看
a
b
α
思辨论证
平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行 。
b??
a∥ b
a ??
a ∥ ?
注明:
1、定理三个条件缺一不可。
2、简记:线线平行,则线面平行。
3、定理告诉我们:
要证线面平行,得在面内找一条线,使线线平行。
b
符号语言
三、抽象概括
直线与平面平行的判定定理:
已知:空间四边形ABCD中,E,F分别是AB,DA的中点。
求证:EF//平面BCD
例1 求证:空间四边形相邻两边中点的连线平行于经过另外两边所在的平面
符号语言:
C
D
B
E
F
A
四、定理应用
A
B
C
D
E
F
例1 求证:空间四边形相邻两边中点的连线平行于经过另外两边所在的平面.
已知:空间四边形ABCD中,E,F分别AB,AD的中点.
求证:EF//平面BCD.
证明:连接BD.
因为 AE=EB , AF=FD,
所以 EF//BD(三角形中位线的性质)
因为
由直线与平面平行的判断定理得
EF//平面BCD.
规范答题参考
1.如图,在空间四边形ABCD中,E、F分
别为AB、AD上的点,若 , 则EF
与平面BCD的位置关系是 ____________.
EF//平面BCD
变式训练:
A
B
C
D
E
F
练习1:如图,长方体 中,
①与 平行的平面是 ____________________________
②与 平行的平面是____________________________
③与 平行的平面是________________________
五、学以致用
分析:要证BD1//平面AEC,
即要在平面AEC内找一条直线与BD1平行.
练习2. 如图,正方体ABCD-A1B1C1D1中,E为DD1的中点.
求证: BD1∥平面AEC
F
E
D1
B1
A1
D
B
A
C1
C
证明:
∴EF∥BD1.
∴ BD1 ∥平面AEC.
是DD1 、BD的中点.
∵ 在△ BDD1中,E、F分别
连接BD,交AC于F点,再连接EF.
EF 平面AEC,
∩
∵ BD1 平面AEC,
五、学以致用
1、直线与平面平行判定定理:
线(面外)线(面内)平行?线面平行
2、运用定理的关键找平行线。找平行线又经常会用到三角形中位线、梯形的中位线、平行四边形、平行公理。(一般题中有中点再找中点,有分点再找分点得平行关系.)
“一线面内、一线面外、两线平行”
3、数学思想方法:
转化与化归的思想
将线面平行转化为线线平行
将空间问题转化为平面问题
课时小结:
六、课时小结
作业:
1、导学案:能力提升
2、课本P62 3
谢谢
再见
