人教版高中数学必修二点到直线的距离课件(共17张PPT)
文档属性
| 名称 | 人教版高中数学必修二点到直线的距离课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 14.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-08 20:54:28 | ||
图片预览





文档简介
(共16张PPT)
点到直线的距离
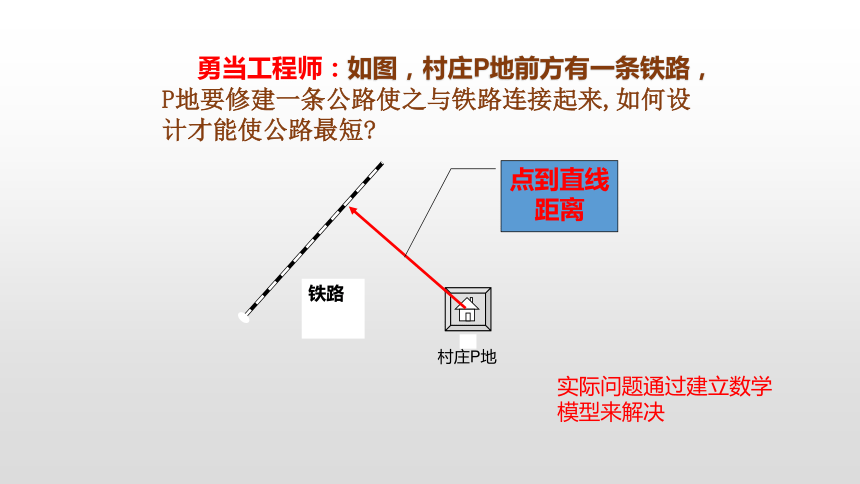
铁路
勇当工程师:如图,村庄P地前方有一条铁路,P地要修建一条公路使之与铁路连接起来,如何设计才能使公路最短?
点到直线距离
村庄P地
实际问题通过建立数学模型来解决
学习目标:
1.理解点到直线的距离公式的推导方法
2.领悟公式推导及优化过程所用的数学思想
3.掌握点到直线的距离公式的应用
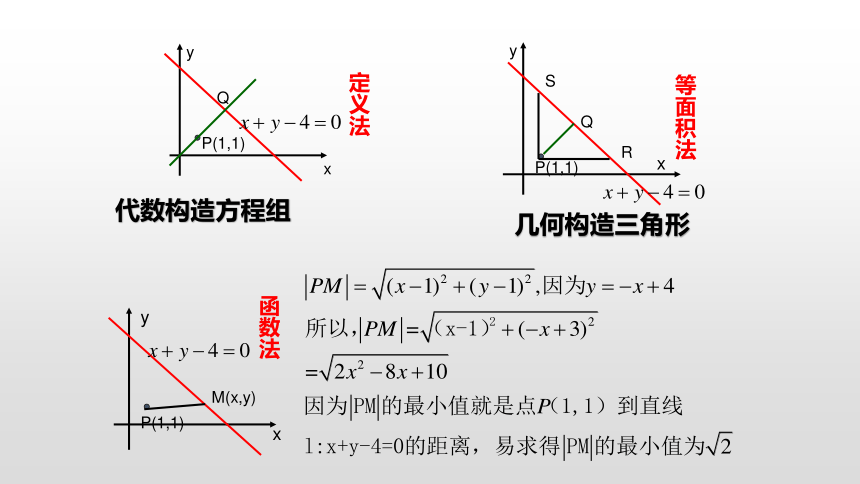
学案点评:求点P(1,1)到直线 的距离
x
y
P(1,1)
0
P(1,1)
Q
x
y
P(1,1)
S
R
Q
x
y
P(1,1)
M(x,y)
x
y
定义法
等面积法
函数法
代数构造方程组
几何构造三角形
l:Ax+By+C=0,
Ax+By+C=0,
Bx-Ay-Bx0+Ay0=0
探究一:点到直线的距离公式的推导方法(定义法)
问题:求点P(x0 ,y 0)到直线l:Ax+By+C=0(A≠0,B≠0)的距离
Q
x
y
o
解法1:
联立方程
A(x1 -x0)+B( y1 -y0)= -Ax0-By0-C ------- ②
B(x1 -x0)–A( y1 -y0)=0 -------------①
①2+②2:(A2+B2)[(x1 -x0)2+( y1 -y0)2]=(Ax0+By0+C)2
交点Q(x1,y1 )满足
B(x1 -x0)–A( y1 -y0)=0
Q
x
y
o
探究:一:点到直线的距离公式的推导方法(定义法)
提问:观察两点之间的距离公式
则
的特征,能否不求Q点坐标而得出结果呢?
,l:Ax+By+C=0
解法2:
O
x
y
点到直线的距离
三角形边上的高
三角形的面积
构造什么样的三角形?
问题:求点P(x0 ,y 0)到直线l:Ax+By+C=0(A≠0,B≠0)的距离
提问:如何想到构造三角形呢?
探究二:点到直线的距离公式的推导方法(等面积法)
P(x0,y0)
S
R
Q
x
y
问题:求点P(x0 ,y 0)到直线l:Ax+By+C=0的距离。
探究二:点到直线的距离公式的推导方法(等面积法)
当直线l 的方程Ax+By+C=0中A=0时:
x
y
o
P0(x0,y0)
Q
.
l :By+C=0,
y=-
C
B
|y0-yQ|=
|By0+C|
|B|
x
y
o
P0(x0,y0)
Q
.
当直线l 的方程Ax+By+C=0中B=0时:
l :Ax+C=0,
x=-
C
A
|PQ|=
C
B
=
y0+
|x0-xQ|=
|Ay0+C|
|A|
|PQ|=
C
A
=
x0+
问题:求点P(x0 ,y 0)到直线l:Ax+By+C=0(A=0或B=0)的距离。
数形结合
解:(1)根据点到直线的距离公式,得
(2)根据点到直线的距离公式,得
探究三:点到直线的距离公式的应用
例1.求点 P ( -1, 2 ) 到下列直线的距离:
⑴ y = -2 x + 10 ⑵ 3 x =2
例2、 已知点A(3,4),B(6,0),C(-5,-2),
求三角形ABC的面积。
B(6,0)
A(3,4)
C(-5,-2)
x
y
o
h
探究三:点到直线的距离公式的应用
变式练习:
( )
( )
D
B
小结:
1.公式的推导选择了哪些方法?
2.本节课学习了哪些数学思想方法?
课后作业:
必做题:习题3.3 A组第9题; B组第2,4题
选做题:课下搜集点到直线距离公式的
推导方法,并整理成文稿。
谢谢大家!
点到直线的距离
铁路
勇当工程师:如图,村庄P地前方有一条铁路,P地要修建一条公路使之与铁路连接起来,如何设计才能使公路最短?
点到直线距离
村庄P地
实际问题通过建立数学模型来解决
学习目标:
1.理解点到直线的距离公式的推导方法
2.领悟公式推导及优化过程所用的数学思想
3.掌握点到直线的距离公式的应用
学案点评:求点P(1,1)到直线 的距离
x
y
P(1,1)
0
P(1,1)
Q
x
y
P(1,1)
S
R
Q
x
y
P(1,1)
M(x,y)
x
y
定义法
等面积法
函数法
代数构造方程组
几何构造三角形
l:Ax+By+C=0,
Ax+By+C=0,
Bx-Ay-Bx0+Ay0=0
探究一:点到直线的距离公式的推导方法(定义法)
问题:求点P(x0 ,y 0)到直线l:Ax+By+C=0(A≠0,B≠0)的距离
Q
x
y
o
解法1:
联立方程
A(x1 -x0)+B( y1 -y0)= -Ax0-By0-C ------- ②
B(x1 -x0)–A( y1 -y0)=0 -------------①
①2+②2:(A2+B2)[(x1 -x0)2+( y1 -y0)2]=(Ax0+By0+C)2
交点Q(x1,y1 )满足
B(x1 -x0)–A( y1 -y0)=0
Q
x
y
o
探究:一:点到直线的距离公式的推导方法(定义法)
提问:观察两点之间的距离公式
则
的特征,能否不求Q点坐标而得出结果呢?
,l:Ax+By+C=0
解法2:
O
x
y
点到直线的距离
三角形边上的高
三角形的面积
构造什么样的三角形?
问题:求点P(x0 ,y 0)到直线l:Ax+By+C=0(A≠0,B≠0)的距离
提问:如何想到构造三角形呢?
探究二:点到直线的距离公式的推导方法(等面积法)
P(x0,y0)
S
R
Q
x
y
问题:求点P(x0 ,y 0)到直线l:Ax+By+C=0的距离。
探究二:点到直线的距离公式的推导方法(等面积法)
当直线l 的方程Ax+By+C=0中A=0时:
x
y
o
P0(x0,y0)
Q
.
l :By+C=0,
y=-
C
B
|y0-yQ|=
|By0+C|
|B|
x
y
o
P0(x0,y0)
Q
.
当直线l 的方程Ax+By+C=0中B=0时:
l :Ax+C=0,
x=-
C
A
|PQ|=
C
B
=
y0+
|x0-xQ|=
|Ay0+C|
|A|
|PQ|=
C
A
=
x0+
问题:求点P(x0 ,y 0)到直线l:Ax+By+C=0(A=0或B=0)的距离。
数形结合
解:(1)根据点到直线的距离公式,得
(2)根据点到直线的距离公式,得
探究三:点到直线的距离公式的应用
例1.求点 P ( -1, 2 ) 到下列直线的距离:
⑴ y = -2 x + 10 ⑵ 3 x =2
例2、 已知点A(3,4),B(6,0),C(-5,-2),
求三角形ABC的面积。
B(6,0)
A(3,4)
C(-5,-2)
x
y
o
h
探究三:点到直线的距离公式的应用
变式练习:
( )
( )
D
B
小结:
1.公式的推导选择了哪些方法?
2.本节课学习了哪些数学思想方法?
课后作业:
必做题:习题3.3 A组第9题; B组第2,4题
选做题:课下搜集点到直线距离公式的
推导方法,并整理成文稿。
谢谢大家!
