人教版数学八年级下册 第十八章18.2.1矩形讲义学案(习题含答案)
文档属性
| 名称 | 人教版数学八年级下册 第十八章18.2.1矩形讲义学案(习题含答案) | 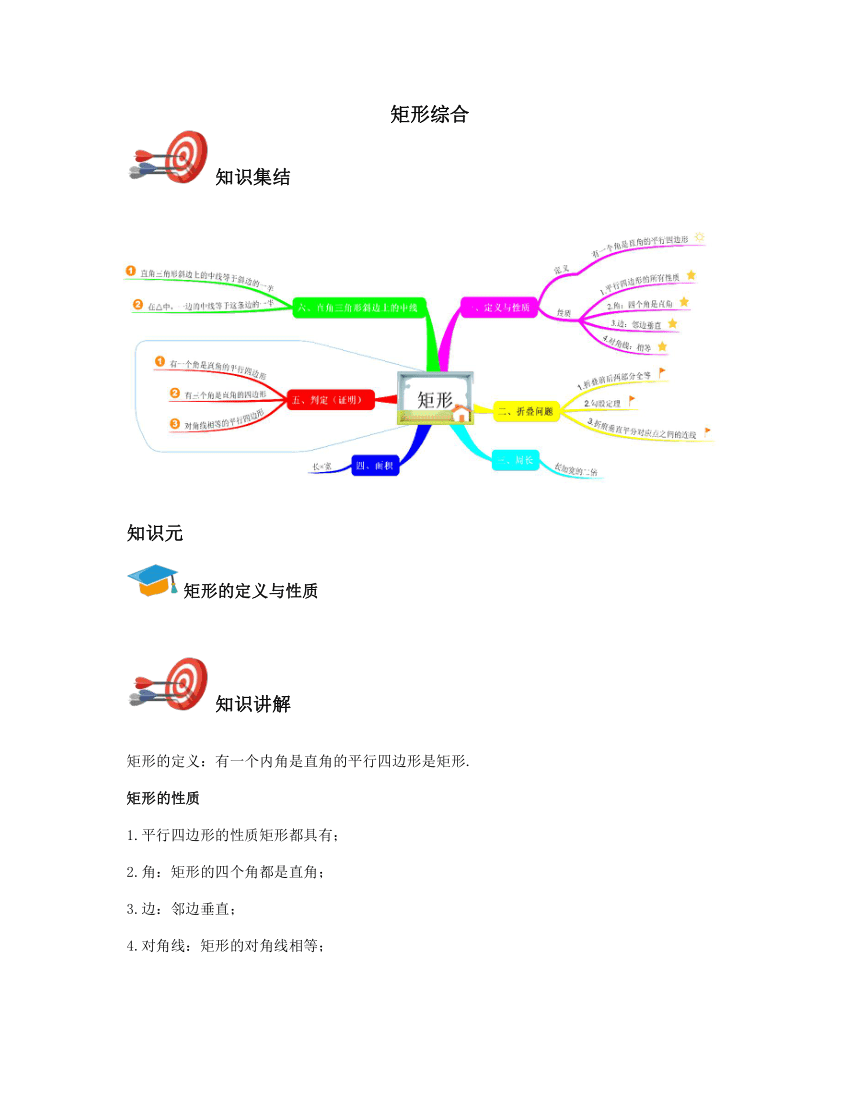 | |
| 格式 | zip | ||
| 文件大小 | 702.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-07 01:20:01 | ||
图片预览




文档简介
矩形综合
知识集结
知识元
矩形的定义与性质
知识讲解
矩形的定义:有一个内角是直角的平行四边形是矩形.
矩形的性质
1.平行四边形的性质矩形都具有;
2.角:矩形的四个角都是直角;
3.边:邻边垂直;
4.对角线:矩形的对角线相等;
5.矩形是轴对称图形,又是中心对称图形.它有2条对称轴,分别是每组对边中点连线所在的直线;对称中心是两条对角线的交点.
例题精讲
矩形的定义与性质
例1.
有一个四边形ABCD是矩形,则下列不一定正确的是( )
A.AD∥BC B.AB=CD
C.对角线AC与BD互相平分 D.对角线AC与BD互相垂直
【答案】D
【解析】
题干解析:
矩形的概念与性质可得,矩形的对角线不一定垂直。
例2.
如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的对角线AC的长是( )
A.2 B.4 C. D.
【答案】B
【解析】
题干解析:
由矩形ABCD的性质得OA=OB,又∠AOB=60°,AB=2,
∴△OAB是等边三角形,
∴OA=AB=2,
∴AC=4.
例3.
如图,矩形ABCD中,AB=3,BC=5过对角线交点O作OEAC 交AD于E则AE的长是( )
A.1.6 B.2.5 C.3 D.3.4
【答案】D
【解析】
题干解析:
连接EC,∵四边形是ABCD矩形,∴OA=OC, ∵OEAC,设AE=x,在Rt△ECD中,由勾股定理得解得x=3.4.
矩形性质的应用
知识讲解
通过画图,识记矩形的定义及相关性质,根据题意解决问题.
例题精讲
矩形性质的应用
例1.
如图,矩形ABCD中,对角线AC,BD相交于点O,,AB=5,则AD的长是( )
A. B. C.5 D.10
【答案】A
【解析】
题干解析:
四边形ABCD是矩形,
又,
是等边三角形,
,
.故选A.
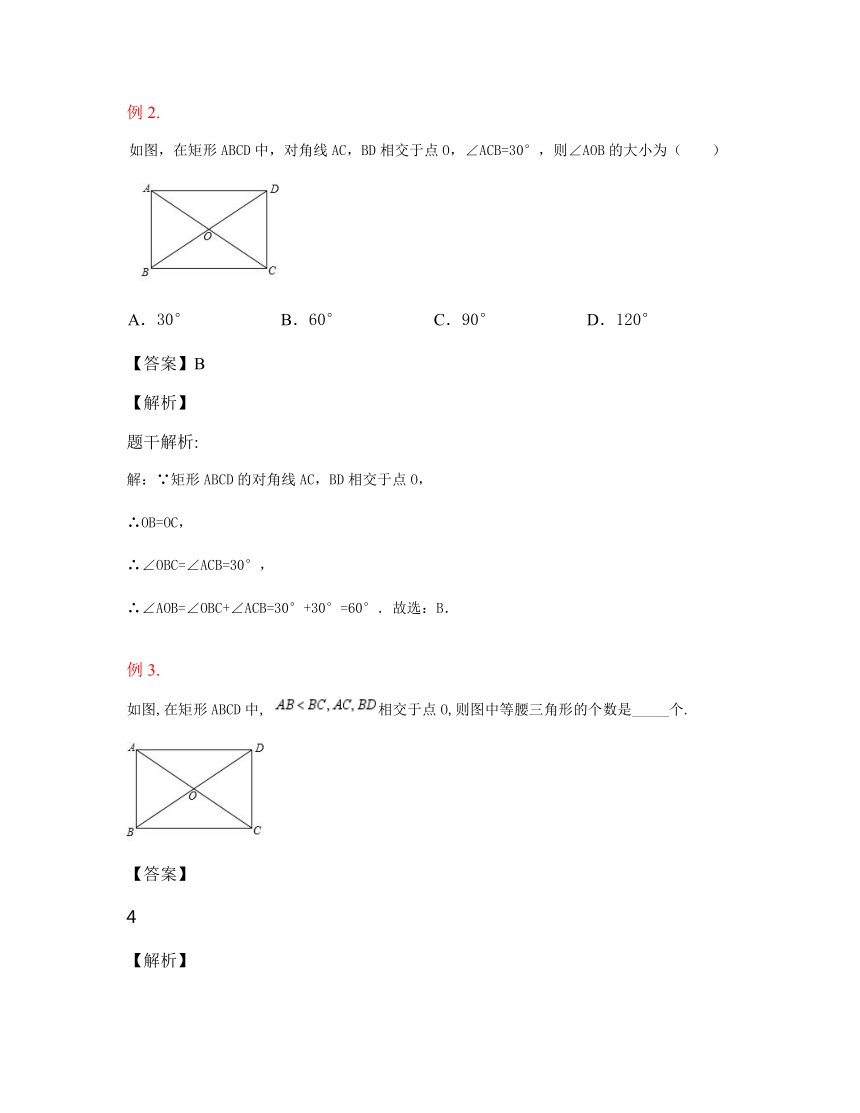
例2.
如图,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,则∠AOB的大小为( )
A.30° B.60° C.90° D.120°
【答案】B
【解析】
题干解析:
解:∵矩形ABCD的对角线AC,BD相交于点O,
∴OB=OC,
∴∠OBC=∠ACB=30°,
∴∠AOB=∠OBC+∠ACB=30°+30°=60°.故选:B.
例3.
如图,在矩形ABCD中, 相交于点O,则图中等腰三角形的个数是_____个.
【答案】
4
【解析】
题干解析:四边形ABCD是矩形,,都是等腰三角形
例4.
矩形ABCD 的对角线AC,BD 相交于点 ,则 的周长为______.
【答案】
12
【解析】
题干解析:∵四边形ABCD是矩形,AC=8,,是等边三角形的周长是4+4+4=12
折叠问题
知识讲解
对于折叠问题,首先应该明白折叠前后的两部分全等,通过全等得到对应角和对应边相等,遇到求边的问题,通常我们会设X,根据勾股定理来列方程求得。
?
例题精讲
折叠问题
例1.
如图,将矩形ABCD沿对角线BD折叠,使点C和点C′重合,若AB=2,则C′D的长为( )
A.1 B.2 C.3 D.4
【答案】B
【解析】
题干解析:
解:在矩形ABCD中,CD=AB,
∵矩形ABCD沿对角线BD折叠后点C和点C′重合,
∴C′D=CD,
∴C′D=AB,
∵AB=2,
∴C′D=2.故选B.
例2.
一张矩形纸片ABCD,长边AD=10cm,若将纸片沿DE折叠,使DC落在DA上,点C的对应点为点F,若BE=6cm,则CD的长为( )
A.4cm B.6cm C.8cm D.10cm
【答案】A
【解析】
题干解析:
由折叠知DC=DF,四边形CDFE为正方形,∴CD=CE=BC-BE=10-6=4(cm)
例3.
如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=20°,那么∠EFC′的度数为 度.
【答案】
125
【解析】
题干解析:有折叠可得四边形FCDE≌四边形FC′BF∴∠BEF=∠DEF,∠EFC=∠EFC′∵∠ABE=20°∴∠EBC=70°∵矩形ABCD中AD∥BC∴∠EBC=∠AEB=70°∴∠BEF=∠FED= (180°-70°)=55°∴∠EFC′=∠EFC=180°-55°=125°
矩形的周长
知识讲解
矩形的周长等于长加宽的二倍.
例题精讲
矩形的周长
例1.
在矩形ABCD中,对角线AC,BD相交于点O,若对角线AC=10cm,边BC=8cm,则△ABO的周长为( )
A.18 B.16 C.20 D.22
【答案】B
【解析】
题干解析:
根据矩形的性质得AC=2OA,BD=2OB,AC=BD,∠ABC=90°,在Rt△ABC中,由勾股定理得出AC=6,求出OA=OB=5,代入OA+OB+AB求出即可。
例2.
矩形的对角线长为两条邻边之比是2∶3,则矩形的周长是___________.
【答案】
20
【解析】
题干解析:根据矩形的性质得到△ABC是直角三角形,对角线长AC=,设AB=2x,BC=3x由勾股定理得:,解得x=2
例3.
如图,矩形ABCD中,AB=3,BC=4,则图中五个小矩形的周长之和为 .
【答案】
14
【解析】
题干解析:解:将五个小矩形的所有上边平移至AD,所有下边平移至BC,所有左边平移至AB,所有右边平移至CD,则五个小矩形的周长之和=2(AB+BC)=2×(3+4)=14.故答案为:14.
矩形的面积
知识讲解
矩形的面积等于长×宽,求阴影部分的面积时需要我们进行转化,或者分割。
例题精讲
矩形的面积
例1.
如图,周长为68的矩形ABCD被分成7个全等的矩形,则矩形ABCD的面积为( ).
A.98 B.196 C.280 D.284
【答案】C
【解析】
题干解析:
设小矩形的宽为x,长为y,由题意
解得:
∴矩形ABCD的面积=20×14=280
例2.
如图,在矩形ABCD中,点E、F分别在边AB、CD上,BF∥DE,若AD=12cm,AB=7cm,且,则阴影部分面积为______.
【答案】
24
【解析】
题干解析:因为,且,则,则阴影部分的面积.
例3.
如图,在矩形ABCD中E、F分别是AB、CD的中点,P为EF上任意一点(不与E、F重合),已知矩形ABCD的长为4cm,宽为3cm,则图中阴影部分的面积是______.
【答案】
6
【解析】
题干解析:根据题意观察图形可知,关于对称,∴ ,∴图中阴影部分的面积即是长方形面积的一半,∴图中阴影部分的面积=.
例4.
如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中矩形AMKP的面积S1与矩形的面QCNK积S2的大小关系是:______.(用“大于”,“小于”,“等于”填写)
【答案】
等于
【解析】
题干解析:∵四边形是矩形,四边形是矩形,四边形是矩形,∴的面积=的面积,的面积=的面积,的面积的面积,的面积的面积的面积的面积的面积的面积,∴
矩形的判定
知识讲解
1.矩形的定义:有一个角是直角的平行四边形是矩形;
2.有三个角是直角的四边形是矩形;
3.对角线相等的平行四边形是矩形(或“对角线互相平分且相等的四边形是矩形”).
例题精讲
矩形的判定
例1.
平行四边形ABCD 中,AC 交BD 于点O ,再添加一个条件,仍不能判定四边形ABCD 是矩形的是( )
A.AB=CD B.OA=OB C.AC=BD D.
【答案】A
【解析】
题干解析:
矩形的判定定理有:
(1)有一个角是直角的平行四边形是矩形.
(2)有三个角是直角的四边形是矩形.
(3)对角线互相平分且相等的四边形是矩形.据此判断.
根据矩形的判定定理(有一个角是直角的平行四边形是矩形)可得
可证四边形ABCD 是矩形.故D不正确.
矩形的对角线相等且相互平分,OA=OB,AC=BD可证四边形ABCD为矩形,故B不正确,C不正确.
例2.
如图,在△ABC中,AB=AC ,将△ABC绕点C 旋转180°得到△EFC,连接AE,BF .当∠ACB为______度时,四边形ABFE 为矩形.
【答案】
60
【解析】
题干解析:如果四边形ABFE为矩形,根据矩形的性质,那么AF=BE,AC=BC,又因为AC=AB,那么三角形ABC是等边三角形,所以.故答案为60.
例3.
如图,将?ABCD的边AB延长到点E,使BE=AB,连接DE,交边BC于点F.
(1)求证:△BEF≌△CDF;
(2)连接BD、CE,若∠BFD=2∠A,求证:四边形BECD是矩形.
【答案】
(1)证明:∵四边形ABCD是平行四边形,∵AB=CD,AB∥CD.∵BE=AB,∴BE=CD.∵AB∥CD,∴∠BEF=∠CDF,∠EBF=∠DCF,在△BEF与△CDF中,∵ ,∴△BEF≌△CDF(ASA);(2)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∠A=∠DCB,∵AB=BE,∴CD=EB,∴四边形BECD是平行四边形,∴BF=CF,EF=DF,∵∠BFD=2∠A,∴∠BFD=2∠DCF,∴∠DCF=∠FDC,∴DF=CF,∴DE=BC,∴四边形BECD是矩形.
【解析】
题干解析:(1)利用平行四边形对边平行且相等得到对应的边和角相等,用角边角即可证得△BEF≌△CDF全等(2)本题用一组对边平行且相等的四边形是平行四边形;对角线相等的平行四边形是矩形,即可证得四边形BECD是矩形。
矩形的判定(证明题)
知识讲解
①证明一个四边形是矩形,若题设条件与这个四边形的对角线有关,通常证这个四边形的对角线相等;
②题设中出现多个直角或垂直时,常采用“三个角是直角的四边形是矩形”来判定矩形.
例题精讲
矩形的判定(证明题)
例1.
如图,在矩形ABCD中,E、F分别是边AB、CD的中点,连接AF,CE.
(1)求证:△BEC≌△DFA;
(2)求证:四边形AECF是平行四边形.
【答案】
证明:(1)∵四边形ABCD是矩形,∴AB=CD,AD=BC,又∵E、F分别是边AB、CD的中点,∴BE=DF,∵在△BEC和△DFA中,,∴△BEC≌△DFA(SAS).(2)由(1)得,CE=AF,AD=BC,故可得四边形AECF是平行四边形.
【解析】
题干解析:(1)根据E、F分别是边AB、CD的中点,可得出BE=DF,继而利用SAS可判断△BEC≌△DFA;(2)由(1)的结论,可得CE=AF,继而可判断四边形AECF是平行四边形.
例2.
如图,AB=CD=ED,AD=EB,BE⊥DE,垂足为E.
(1)求证:△ABD≌△EDB;
(2)只需添加一个条件,即 等,可使四边形ABCD为矩形.请加以证明.
【答案】
证明:(1)∵AB=CD=ED,AD=EB,BD=BD,∴△ABD≌△EDB;(2)根据矩形的判定得,可添加AB∥CD;∵AB=CD=ED,AB∥CD,∴四边形ABCD是平行四边形.∵BE⊥DE,∴∠E=90°.∵△ABD≌△EDB,∴∠A=∠E=90°.∴平行四边形ABCD是矩形.
【解析】
题干解析:(1)题中条件给的很充分,可根据SSS直接判定三角形全等.(2)本题应先证明四边形ABCD为平行四边形,再通过△ABD≌△EDB得到∠A=∠E=90°,从而说明平行四边形ABCD是矩形.
例3.
如图,在□ABCD中,E、F为BC上的两点,且BE=CF,AF=DE.
求证:(1)△ABF≌△DCE;
(2)四边形ABCD是矩形.
【答案】
解:(1)∵BE=CF,BF=BE+EF,CE=CF+EF,∴BF=CE.∵四边形ABCD是平行四边形,∴AB=DC.在△ABF和△DCE中,∵AB=DC,BF=CE,AF=DE,∴△ABF≌△DCE.(2)解法一:∵△ABF≌△DCE,∴∠B=∠C,∵四边形ABCD是平行四边形,∴AB∥CD.∴∠B+∠C=180°∴∠B=∠C=90°所以四边形ABCD是矩形.解法二:连接AC,DB.∵△ABF≌△DCE,∴∠AFB=∠DEC,∴∠AFC=∠DEB.在△AFC和△DEB中,∵AF=DE, ∠AFC=∠DEB,CF=BE.∴△AFC≌△DEB,∴AC=DB.∵四边形ABCD是平行四边形,∴四边形ABCD是矩形.
【解析】
题干解析:运用平行四边形的性质得全等,还要求准确记忆矩形的判定。
直角三角形斜边上的中线
知识讲解
直角三角形斜边上的中线等于斜边的一半;三角形中,一边的中线等于这条边的一半时,这个三角形是直角三角形。(在小题中可以直接使用,证明题中使用时要先证明)
30°的直角三角形中,30°所对的直角边等于斜边的一半;结合以上直角三角形的性质可以得到等边三角形。
例题精讲
直角三角形斜边上的中线
例1.
如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( ).
A. B. C. D.
【答案】A
【解析】
题干解析:
由于为的中位线,,从而根据三角形中位线平行于第三边并且等于第三边一半的性质,得;又由于,点为的中点,,从而根据直角三角形斜边上中线等于斜边一半的性质,得.因此.
例2.
如图,∠ACB=90°,D为AB的中点,连接CD并延长到E,使CE=,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为( )
A.6 B.7 C.8 D.10
【答案】C
【解析】
题干解析:
解:∵,为的中点,,
∴.又,
∴,
∴.
又∵,点D是AB的中点,
∴ED是的中位线,
∴BF=2ED=8.故选:C.
例3.
在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=5,则线段DE的长为________.
【答案】
2.5
【解析】
题干解析:解:平分,,,,
当堂练习
单选题
练习1.
有一个四边形ABCD是矩形,下列说法一定正确的是( )
A.AD⊥BC B.AB=BC
C.对角线AC与BD互相平分 D.对角线AC与BD互相垂直
练习2.
如图矩形中,,,点为上一个动点,把沿折叠,当点的对应点落在的角平分线上时,的长为( )
A.或 B.或 C.或 D.或
练习3.
如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
A. B. C. D.
练习4.
如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( ).
A. B. C. D.
练习5.
如图,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别是S1、S2的大小关系是( )
A.S1>S2 B.S1=S2
C.S1<S2 D.3S1=2S2
练习6.
如图,,D为AB的中点,连接CD并延长到E,使,过点B作,与AE的延长线交于点F.若AB=6,则BF的长为( )
A.6 B.7 C.8 D.10
练习7.
如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为( )
A.2 B.2.2 C.2.4 D.2.5
填空题
练习1.
如图,在矩形ABCD中,对角线AC,BD交于点O.已知,,则图中长度为8的线段有______条.
练习2.
如图,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,则∠AOB的大小为______.
练习3.
矩形的对角线长为两条邻边之比是2∶3,则矩形的周长是___________.
练习4.
如图,在矩形中,点分别在边上,,若,且,则阴影部分面积为______.
练习5.
如图,矩形ABCD中,AB=3,BC=4,则图中五个小矩形的周长之和为 .
练习6.
著名画家达芬奇不仅画艺超群,同时还是一个数学家、发明家.他曾经设计过一种圆规如图所示,有两个互相垂直的滑槽(滑槽宽度忽略不计),一根没有弹性的木棒的两端A、B能在滑槽内自由滑动,将笔插入位于木棒中点P处的小孔中,随着木棒的滑动就可以画出一个圆来.若AB=20cm,则画出的圆的半径为_______cm.
练习7.
如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=20°,那么∠EFC′的度数为 度.
解答题
练习1.
已知:如图,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE,CF.
(1)求证:AF=CE;
(2)若AC=EF,试判断四边形AFCE是什么样的四边形,并证明你的结论.
练习2.
如图,将?ABCD的边AB延长到点E,使BE=AB,连接DE,交边BC于点F.
(1)求证:△BEF≌△CDF;
(2)连接BD、CE,若∠BFD=2∠A,求证:四边形BECD是矩形.
单选题:CACAB CC
填空题:6,60°,20,24,14,10,125
解答题
练习1:【答案】
(1)证明:在△ADF和△CDE中,∵AF∥BE,∴∠FAD=∠ECD.又∵D是AC的中点,∴AD=CD.∵∠ADF=∠CDE,∴△ADF≌△CDE.∴AF=CE.(2)解:若AC=EF,则四边形AFCE是矩形.证明:由(1)知:AF=CE,AF∥CE,∴四边形AFCE是平行四边形.又∵AC=EF,∴平行四边形AFCE是矩形.
【解析】
题干解析:(1)可通过全等三角形来证明简单的线段相等.△ADF和△CDE中,已知了AD=CD,∠ADF=∠CDE,AF∥BE,因此不难得出两三角形全等,进而可得出AF=CE.(2)需先证明四边形AFCE是平行四边形,那么对角线相等的平行四边形是矩形.
练习2:【答案】
(1)证明:∵四边形ABCD是平行四边形,∵AB=CD,AB∥CD.∵BE=AB,∴BE=CD.∵AB∥CD,∴∠BEF=∠CDF,∠EBF=∠DCF,在△BEF与△CDF中,∵,∴△BEF≌△CDF(ASA);(2)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∠A=∠DCB,∵AB=BE,∴CD=EB,∴四边形BECD是平行四边形,∴BF=CF,EF=DF,∵∠BFD=2∠A,∴∠BFD=2∠DCF,∴∠DCF=∠FDC,∴DF=CF,∴DE=BC,∴四边形BECD是矩形.
【解析】
题干解析:(1)利用平行四边形对边平行且相等得到对应的边和角相等,用角边角即可证得△BEF≌△CDF全等(2)本题用一组对边平行且相等的四边形是平行四边形;对角线相等的平行四边形是矩形,即可证得四边形BECD是矩形。
