北师大版八年级数学下册6.1平行四边形的性质课件(共22张)
文档属性
| 名称 | 北师大版八年级数学下册6.1平行四边形的性质课件(共22张) |  | |
| 格式 | zip | ||
| 文件大小 | 447.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-07 09:29:03 | ||
图片预览






文档简介
(共22张PPT)
《数学》( 北师大.七年级 下册 )
八年级下册第六章《平行四边形》
1.平行四边形的性质
2、掌握平行四边形的性质,并能够利用性质进行简单的推理计算。
1、掌握平行四边形有关概念.
学习目标
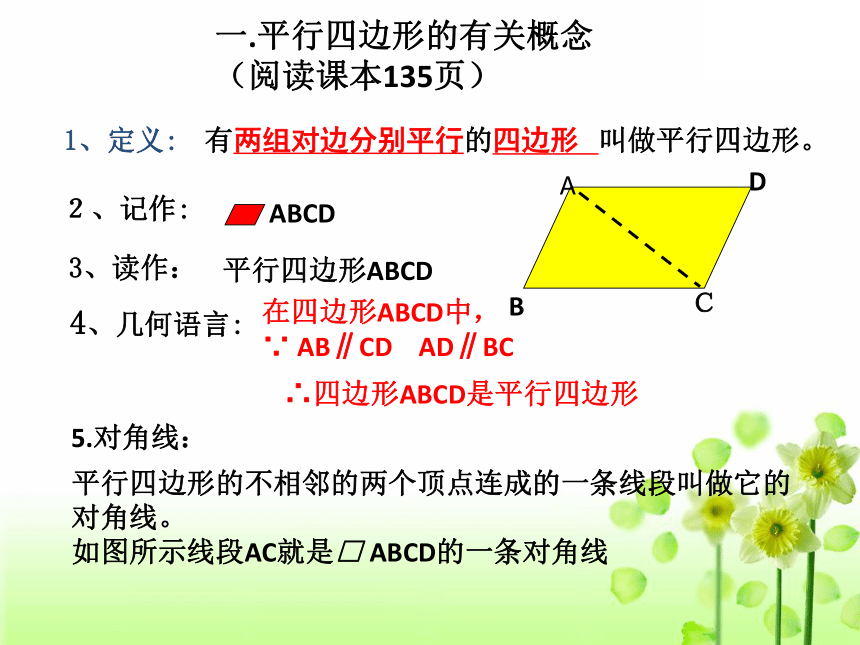
1、定义:
2、记作:
4、几何语言:
∴四边形ABCD是平行四边形
ABCD
在四边形ABCD中,
∵ AB∥CD AD∥BC
3、读作:
有两组对边分别平行的四边形 叫做平行四边形。
平行四边形ABCD
A
B
D
C
一.平行四边形的有关概念 (阅读课本135页)
平行四边形的不相邻的两个顶点连成的一条线段叫做它的对角线。
如图所示线段AC就是□ ABCD的一条对角线
5.对角线:
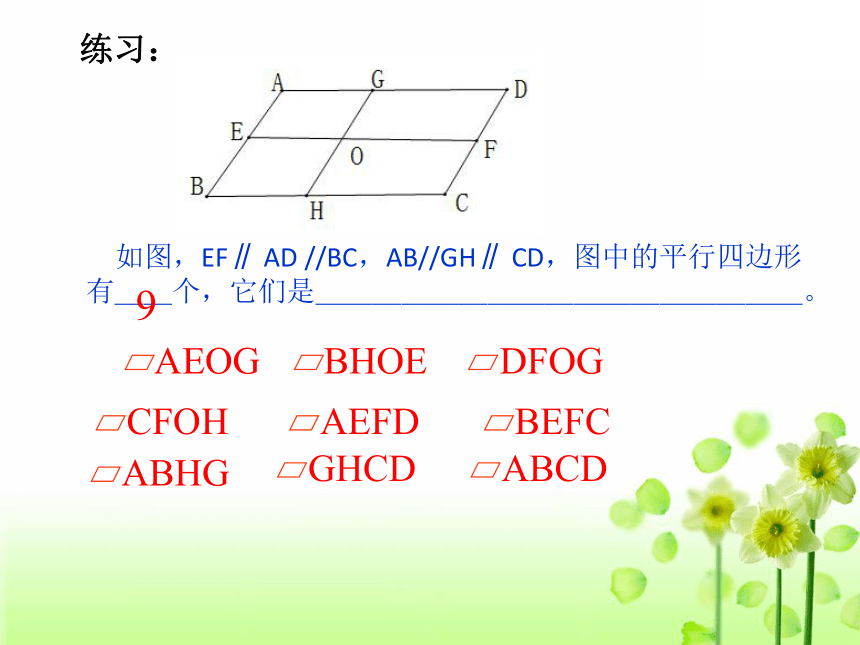
如图,EF∥ AD //BC,AB//GH∥ CD,图中的平行四边形
有__个,它们是_________________。
9
AEOG
DFOG
BHOE
AEFD
CFOH
BEFC
ABCD
GHCD
ABHG
练习:
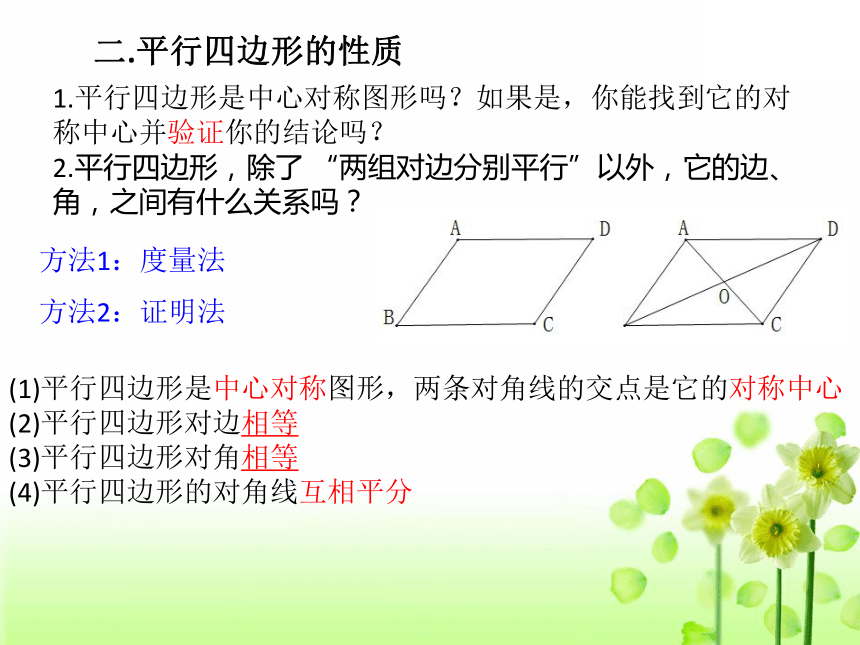
(1)平行四边形是中心对称图形,两条对角线的交点是它的对称中心
(2)平行四边形对边相等
(3)平行四边形对角相等
(4)平行四边形的对角线互相平分
二.平行四边形的性质
1.平行四边形是中心对称图形吗?如果是,你能找到它的对称中心并验证你的结论吗?
2.平行四边形,除了 “两组对边分别平行”以外,它的边、角,之间有什么关系吗?
方法1:度量法
方法2:证明法
即∠ADC=∠ABC
证明:连结BD
在平行四边形ABCD中,
AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2,BD=DB,∠3=∠4
∴ ABC ≌ CDA(ASA)
∴AB=CD,BC=DA,∠A=∠C
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在 ABD 和 CDB中
推理证明
已知:如图, □ ABCD
求证:AB=CD,BC=AD, ∠B= ∠D, ∠A= ∠C
推理证明
已知:如图, □ ABCD,AC,BD相交于点O
求证:OA=0C,OB=OD
证明:
在平行四边形ABCD中,AB//CD,AB=CD
∴∠1=∠2, ∠3=∠4,
∴ △AOB≌ △COD
∴OA=OC,OB=OD
平行四边形的性质
平行四边形
的
平行四边形
的
平行四边形
的
∵四边形ABCD是平行四边形
∴ ∥ , ∥
A
B
C
D
∵四边形ABCD是平行四边形
∴ = , =
∵四边形ABCD是平行四边形
∴ = =
对边平行
AB
CD
AD
BC
AB
CD
AD
BC
∠A
∠B
∠D
∠C ,
对边相等
对角相等
元素 性质 几何语言 图形
边 ? ? ?
?
?
? ?
角 ? ?
对角线 ?对角线互相平分 ∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD ?
1、如图, ABCD中,∠B=50°
则∠A= ;∠C= ;
∠D= .
B
C
D
A
2、□ ABCD中, AB=3cm, BC=5cm, 则AD= ,CD= .
B
C
A
D
3、在□ABCD中,∠A+∠C=120°,
∠B= ;∠D= ;
A
B
C
D
50°
130°
130°
3cm
5cm
120°
120°
练习一:
4.小明用一根36m长的绳子围成了一个平行四边形场地,其中一条边AB长为8m,其他三条边各长多少?
A
B
D
C
解:∵四边形ABCD是平行四边形
∴AB = CD,AD=BC
∵AB=8,
∴CD=8(m)
又AB+BC+CD+AD=36.
∴AD=BC=10(m)
练习二
(1)平行四边形ABCD中,∠A比∠B大20°,则∠C的度数为( )
A.60° B.80° C.100° D.120°
(2)平行四边形ABCD的周长为40cm,△ABC的周长为25cm,
则对角线AC长为( )
A.5cm B.15cm C.6cm D.16cm
(3)平行四边形ABCD中,对角线AC、BD交于O,
则全等三角形的对数有 。
(4)若平行四边形的一边长为5,则它的两条对角线长可以是( )
A.12和2 B.3和4 C.4和6 D.4和8
C
A
(5)若平行四边形的一边长为5,则它的两条对角线长可以是( )
A.12和2 B.3和4 C.4和6 D.4和8
4
D
D
(6)如图:已知平行四边形ABCD的周长为60 cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长短8cm,
求这个四边形各边长.
19cm, 11cm, 19cm, 11cm
(7)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,OE ⊥BD交AD于点E,连接BE,若平行四边形ABCD的周长为28,则△ABE的周长为( )
A.28 B.24 C.21 D.14
D
例1.如图在□ABCD中对角线AC、BD相交于点O。点E,F分
别在AO,CO上,且AE=CF。
求证:∠EBO=∠FDO。
你有几种证明方法?
例2.在平行四边形ABCD中,∠A=150°,AB=8cm,
BC=10cm,求平行四边形ABCD的面积。
解:过A作AE⊥BC交BC于E,
∵四边形ABCD是平行四边形
∴AD//BC
∴∠BAD+∠B =180°
∵∠BAD =150°
∴∠B =30°
在Rt△ABE中,∠B =30°
∴AE =1/2AB=4
∴平行四边形ABCD的面积=4×10=40cm2
例3.已知:如图,在平行四边形ABCD中,平行于对
角线AC的直线MN分别交DA,DC的延长线于M,N,
交BA,BC于点P,点B,你能说明MQ=NP吗?
解:∵四边形ABCD是平行四边形
∴AD//BC,AB//CD 即AM//CQ
又∵AC//MN 即AC//MQ
∴四边形MQCA是平行四边形
∴MQ=AC
同理 NP=AC
∴MQ=NP
例4.已知,如图,平行四边形ABCD的对角线AC与BD相交于点O,过点O的直线与AD,BC分别相交于点E,F.
求证:OE=OF
练习:名校课堂99页15题
(2)过平行四边形的中心O,作一条直线与平行四边形对边(或对边的延长线)相交于点E,F,则OE=OF
练习:课本139页第4题
这些直线都过平行四边形的中心
过平行四边形的中心的任意一条直线都可以把平行四边形分成相等的两部分
名校课堂97页11
在平行四边形ABCD中,AE平分∠BAD交BC于点E,DF平分∠ADC交边BC于点F,若AD=11,EF=5,则AB= .
3或8
如图,平行四边形ABCD的对角线AC,BD相交于点O,AC⊥AB,
AB=2,且AO:BO=2:3,
(1)求AC的长度;
(2)求平行四边形的面积。
如图,已知在平行四边形ABCD中,对角线BD⊥AB,∠A=30°,DE平分∠ADC交AB的延长线于点E,连接CE.
(1)求证:AD=AE;
(2)已知AD=12,连接AC交BD于点O,画出图形,并求AC的长度。
14.如图,已知在平行四边形ABCD中,对角线BD⊥AB,∠A=30°,DE平分∠ADC交AB的延长线于点E,连接CE.
(1)求证:AD=AE;
(2)已知AD=12,连接AC交BD于点O,画出图形,并求AC的长度。
《数学》( 北师大.七年级 下册 )
八年级下册第六章《平行四边形》
1.平行四边形的性质
2、掌握平行四边形的性质,并能够利用性质进行简单的推理计算。
1、掌握平行四边形有关概念.
学习目标
1、定义:
2、记作:
4、几何语言:
∴四边形ABCD是平行四边形
ABCD
在四边形ABCD中,
∵ AB∥CD AD∥BC
3、读作:
有两组对边分别平行的四边形 叫做平行四边形。
平行四边形ABCD
A
B
D
C
一.平行四边形的有关概念 (阅读课本135页)
平行四边形的不相邻的两个顶点连成的一条线段叫做它的对角线。
如图所示线段AC就是□ ABCD的一条对角线
5.对角线:
如图,EF∥ AD //BC,AB//GH∥ CD,图中的平行四边形
有__个,它们是_________________。
9
AEOG
DFOG
BHOE
AEFD
CFOH
BEFC
ABCD
GHCD
ABHG
练习:
(1)平行四边形是中心对称图形,两条对角线的交点是它的对称中心
(2)平行四边形对边相等
(3)平行四边形对角相等
(4)平行四边形的对角线互相平分
二.平行四边形的性质
1.平行四边形是中心对称图形吗?如果是,你能找到它的对称中心并验证你的结论吗?
2.平行四边形,除了 “两组对边分别平行”以外,它的边、角,之间有什么关系吗?
方法1:度量法
方法2:证明法
即∠ADC=∠ABC
证明:连结BD
在平行四边形ABCD中,
AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2,BD=DB,∠3=∠4
∴ ABC ≌ CDA(ASA)
∴AB=CD,BC=DA,∠A=∠C
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在 ABD 和 CDB中
推理证明
已知:如图, □ ABCD
求证:AB=CD,BC=AD, ∠B= ∠D, ∠A= ∠C
推理证明
已知:如图, □ ABCD,AC,BD相交于点O
求证:OA=0C,OB=OD
证明:
在平行四边形ABCD中,AB//CD,AB=CD
∴∠1=∠2, ∠3=∠4,
∴ △AOB≌ △COD
∴OA=OC,OB=OD
平行四边形的性质
平行四边形
的
平行四边形
的
平行四边形
的
∵四边形ABCD是平行四边形
∴ ∥ , ∥
A
B
C
D
∵四边形ABCD是平行四边形
∴ = , =
∵四边形ABCD是平行四边形
∴ = =
对边平行
AB
CD
AD
BC
AB
CD
AD
BC
∠A
∠B
∠D
∠C ,
对边相等
对角相等
元素 性质 几何语言 图形
边 ? ? ?
?
?
? ?
角 ? ?
对角线 ?对角线互相平分 ∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD ?
1、如图, ABCD中,∠B=50°
则∠A= ;∠C= ;
∠D= .
B
C
D
A
2、□ ABCD中, AB=3cm, BC=5cm, 则AD= ,CD= .
B
C
A
D
3、在□ABCD中,∠A+∠C=120°,
∠B= ;∠D= ;
A
B
C
D
50°
130°
130°
3cm
5cm
120°
120°
练习一:
4.小明用一根36m长的绳子围成了一个平行四边形场地,其中一条边AB长为8m,其他三条边各长多少?
A
B
D
C
解:∵四边形ABCD是平行四边形
∴AB = CD,AD=BC
∵AB=8,
∴CD=8(m)
又AB+BC+CD+AD=36.
∴AD=BC=10(m)
练习二
(1)平行四边形ABCD中,∠A比∠B大20°,则∠C的度数为( )
A.60° B.80° C.100° D.120°
(2)平行四边形ABCD的周长为40cm,△ABC的周长为25cm,
则对角线AC长为( )
A.5cm B.15cm C.6cm D.16cm
(3)平行四边形ABCD中,对角线AC、BD交于O,
则全等三角形的对数有 。
(4)若平行四边形的一边长为5,则它的两条对角线长可以是( )
A.12和2 B.3和4 C.4和6 D.4和8
C
A
(5)若平行四边形的一边长为5,则它的两条对角线长可以是( )
A.12和2 B.3和4 C.4和6 D.4和8
4
D
D
(6)如图:已知平行四边形ABCD的周长为60 cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长短8cm,
求这个四边形各边长.
19cm, 11cm, 19cm, 11cm
(7)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,OE ⊥BD交AD于点E,连接BE,若平行四边形ABCD的周长为28,则△ABE的周长为( )
A.28 B.24 C.21 D.14
D
例1.如图在□ABCD中对角线AC、BD相交于点O。点E,F分
别在AO,CO上,且AE=CF。
求证:∠EBO=∠FDO。
你有几种证明方法?
例2.在平行四边形ABCD中,∠A=150°,AB=8cm,
BC=10cm,求平行四边形ABCD的面积。
解:过A作AE⊥BC交BC于E,
∵四边形ABCD是平行四边形
∴AD//BC
∴∠BAD+∠B =180°
∵∠BAD =150°
∴∠B =30°
在Rt△ABE中,∠B =30°
∴AE =1/2AB=4
∴平行四边形ABCD的面积=4×10=40cm2
例3.已知:如图,在平行四边形ABCD中,平行于对
角线AC的直线MN分别交DA,DC的延长线于M,N,
交BA,BC于点P,点B,你能说明MQ=NP吗?
解:∵四边形ABCD是平行四边形
∴AD//BC,AB//CD 即AM//CQ
又∵AC//MN 即AC//MQ
∴四边形MQCA是平行四边形
∴MQ=AC
同理 NP=AC
∴MQ=NP
例4.已知,如图,平行四边形ABCD的对角线AC与BD相交于点O,过点O的直线与AD,BC分别相交于点E,F.
求证:OE=OF
练习:名校课堂99页15题
(2)过平行四边形的中心O,作一条直线与平行四边形对边(或对边的延长线)相交于点E,F,则OE=OF
练习:课本139页第4题
这些直线都过平行四边形的中心
过平行四边形的中心的任意一条直线都可以把平行四边形分成相等的两部分
名校课堂97页11
在平行四边形ABCD中,AE平分∠BAD交BC于点E,DF平分∠ADC交边BC于点F,若AD=11,EF=5,则AB= .
3或8
如图,平行四边形ABCD的对角线AC,BD相交于点O,AC⊥AB,
AB=2,且AO:BO=2:3,
(1)求AC的长度;
(2)求平行四边形的面积。
如图,已知在平行四边形ABCD中,对角线BD⊥AB,∠A=30°,DE平分∠ADC交AB的延长线于点E,连接CE.
(1)求证:AD=AE;
(2)已知AD=12,连接AC交BD于点O,画出图形,并求AC的长度。
14.如图,已知在平行四边形ABCD中,对角线BD⊥AB,∠A=30°,DE平分∠ADC交AB的延长线于点E,连接CE.
(1)求证:AD=AE;
(2)已知AD=12,连接AC交BD于点O,画出图形,并求AC的长度。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
