沪科版九年级数学下册课件24.8 综合与实践 进球线路与最佳射门角(15张)
文档属性
| 名称 | 沪科版九年级数学下册课件24.8 综合与实践 进球线路与最佳射门角(15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-07 13:57:15 | ||
图片预览






文档简介
课件15张PPT。第二十四章
圆九年级数学沪科版·下册24.8 综合与实践 进球线路与最佳射门角教学目标1.掌握最佳射门角与射门点、球门两主柱三点圆的圆周角;
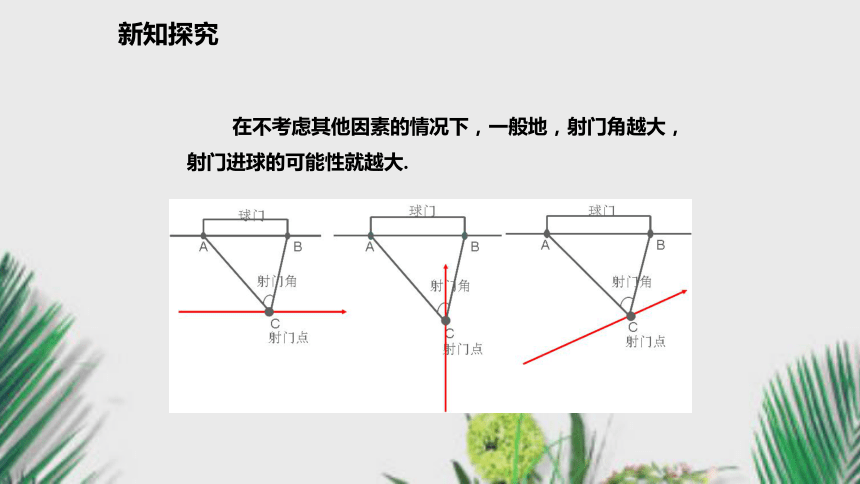
2.理解圆周角定理的实际应用.情景导入新知探究 在不考虑其他因素的情况下,一般地,射门角越大,
射门进球的可能性就越大.新知探究最佳射门角与射门点、球门两主柱三点圆的圆周角1.在同圆或等圆中,同弧或等弧所对的圆周角相等,
相等的圆周角所对的弦也相等.
2.如果⊙O过点A,B,而直线AB同
侧的三点C1,C0,C2分别在⊙O
外,⊙O上和⊙O内,如图,则有
∠AC1B<∠AC0B<∠AC2B.新知探究 简单地说:在弦的同侧,同弧所对的圆外角α,圆
周角β和圆内角θ的大小关系为α<β<θ.新知探究例1 如图,足球运动员在球门AB前横向带球准备射门,
下列说法正确的是( )
A.在C处射门进球的可能性大
B.在D处射门进球的可能性大
C.在C,D两处射门进球的可能性一样大
D.无法判断C,D两处哪处进球的可能性大B新知探究 因为点D距离球门AB的中心比较近,所以∠ADB
大于∠ACB,所以在D处射门进球的可能性大.新知探究例2 如图,点A,B,C表示足球比赛中三个不同的射门
位置,估测图中各角的大小关系,请指出在图中
________点处射门最好.B观察可知∠A<∠C<∠B.故在B点处射门最好.新知探究例3 足球训练场上,教练在球门前画了一个圆圈进行无
人防守的射门训练.如图,甲、乙两名运动员分别
在C,D两处,他们争论不休,都说自己所在的位置
对球门AB的张角大,如果你是教练,请评一评他们
两个人谁的位置对球门AB的张角大?为什么?甲、乙两个人所在的位置对球门
AB的张角一样大.根据圆周角定
理的推论可得∠ADB=∠ACB.解:课堂小结 1、横向跑动时的最佳射门点:
跑动路线和球门AB中垂线的交点
推论1:
最佳射门角的大小与跑动路线l到直线AB的距离有关,当跑动路线l与AB的距离越近,最佳射门角就越大,射门进球的可能性也就越大.
推论2:
如果圆过点A,B,而直线AB同侧的三点C1,C0,C2分别在圆外、圆上、圆内,则有:
圆外角<圆上角<圆内角课堂小结2.直向跑动时的最佳射门点:
(1)直向跑动时,直线l垂直但不穿过球门AB时,
当直线l与过A,B的圆相切时,切点是最佳射门点
(2)直向跑动时,直线l垂直且穿过球门AB时,
当运动员跑动路线垂直穿过球门AB时,射门角越来越大,直线l上没有最佳射门点
课堂小测1 .足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.己知在正方形网格中(每个正方形单位长度都为1),点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射点在( )
A.点C
B.点D或点E
C.线段DE(异于端点)上一点
D.线段CD(异于端点)上一点C课堂小测2.如图,A,B表示球门边框的两端点,C表示射门点,连接AC,BC,∠ACB即为射门角,当球员带球沿直线l跑动时(若l//AB),则射门点C应选在_______处射门角最大( ).
A.点D B.点E C.点M D.点N
C课堂小测3.如图,在△ABC的外接圆中,CP⊥AB,当点C沿CP方向运动时,其点C所对弧AB的张角的变化情况是( )
A.越来越大 B.越来越小 C.不变 D.大于180°A
2.理解圆周角定理的实际应用.情景导入新知探究 在不考虑其他因素的情况下,一般地,射门角越大,
射门进球的可能性就越大.新知探究最佳射门角与射门点、球门两主柱三点圆的圆周角1.在同圆或等圆中,同弧或等弧所对的圆周角相等,
相等的圆周角所对的弦也相等.
2.如果⊙O过点A,B,而直线AB同
侧的三点C1,C0,C2分别在⊙O
外,⊙O上和⊙O内,如图,则有
∠AC1B<∠AC0B<∠AC2B.新知探究 简单地说:在弦的同侧,同弧所对的圆外角α,圆
周角β和圆内角θ的大小关系为α<β<θ.新知探究例1 如图,足球运动员在球门AB前横向带球准备射门,
下列说法正确的是( )
A.在C处射门进球的可能性大
B.在D处射门进球的可能性大
C.在C,D两处射门进球的可能性一样大
D.无法判断C,D两处哪处进球的可能性大B新知探究 因为点D距离球门AB的中心比较近,所以∠ADB
大于∠ACB,所以在D处射门进球的可能性大.新知探究例2 如图,点A,B,C表示足球比赛中三个不同的射门
位置,估测图中各角的大小关系,请指出在图中
________点处射门最好.B观察可知∠A<∠C<∠B.故在B点处射门最好.新知探究例3 足球训练场上,教练在球门前画了一个圆圈进行无
人防守的射门训练.如图,甲、乙两名运动员分别
在C,D两处,他们争论不休,都说自己所在的位置
对球门AB的张角大,如果你是教练,请评一评他们
两个人谁的位置对球门AB的张角大?为什么?甲、乙两个人所在的位置对球门
AB的张角一样大.根据圆周角定
理的推论可得∠ADB=∠ACB.解:课堂小结 1、横向跑动时的最佳射门点:
跑动路线和球门AB中垂线的交点
推论1:
最佳射门角的大小与跑动路线l到直线AB的距离有关,当跑动路线l与AB的距离越近,最佳射门角就越大,射门进球的可能性也就越大.
推论2:
如果圆过点A,B,而直线AB同侧的三点C1,C0,C2分别在圆外、圆上、圆内,则有:
圆外角<圆上角<圆内角课堂小结2.直向跑动时的最佳射门点:
(1)直向跑动时,直线l垂直但不穿过球门AB时,
当直线l与过A,B的圆相切时,切点是最佳射门点
(2)直向跑动时,直线l垂直且穿过球门AB时,
当运动员跑动路线垂直穿过球门AB时,射门角越来越大,直线l上没有最佳射门点
课堂小测1 .足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.己知在正方形网格中(每个正方形单位长度都为1),点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射点在( )
A.点C
B.点D或点E
C.线段DE(异于端点)上一点
D.线段CD(异于端点)上一点C课堂小测2.如图,A,B表示球门边框的两端点,C表示射门点,连接AC,BC,∠ACB即为射门角,当球员带球沿直线l跑动时(若l//AB),则射门点C应选在_______处射门角最大( ).
A.点D B.点E C.点M D.点N
C课堂小测3.如图,在△ABC的外接圆中,CP⊥AB,当点C沿CP方向运动时,其点C所对弧AB的张角的变化情况是( )
A.越来越大 B.越来越小 C.不变 D.大于180°A
