沪科版九年级数学下册:24.4.1 直线与圆的位置关系 课件(共21张PPT)
文档属性
| 名称 | 沪科版九年级数学下册:24.4.1 直线与圆的位置关系 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-07 00:00:00 | ||
图片预览






文档简介
课件21张PPT。第二十四章
圆九年级数学沪科版·下册24.4.1直线与圆的位置关系教学目标1.理解直线与圆有相交、相切、相离三种位置关系.
2.能根据圆心到直线的距离d和圆的半径r之间的数量关系,
判断出直线与圆的位置关系.(重点)
复习导入情境引入太阳要从天边升起来了,便不转眼地望着那里. 果然过了一会儿,在那个地方出现了太阳的小半边脸,红是真红,却没有亮光.这个太阳好像负着重荷似地一步一步,慢慢地努力上升,到了最后,终于冲破了云霞,完全跳出了海面,颜色红得非常可爱.
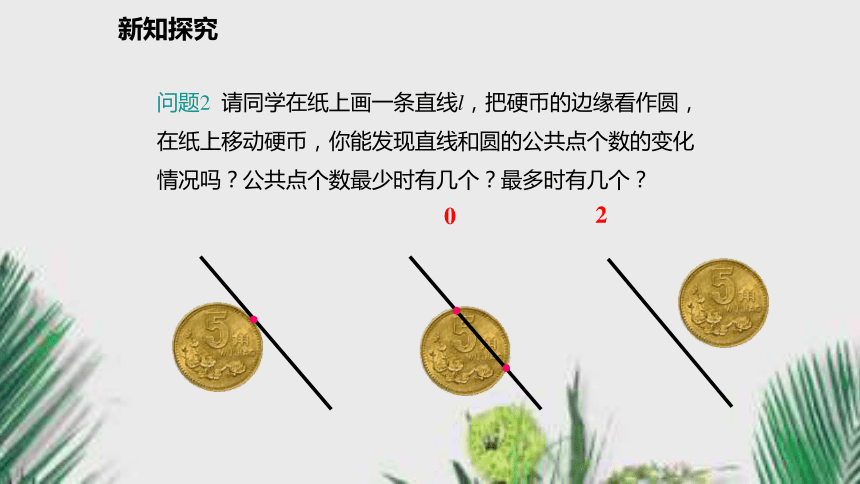
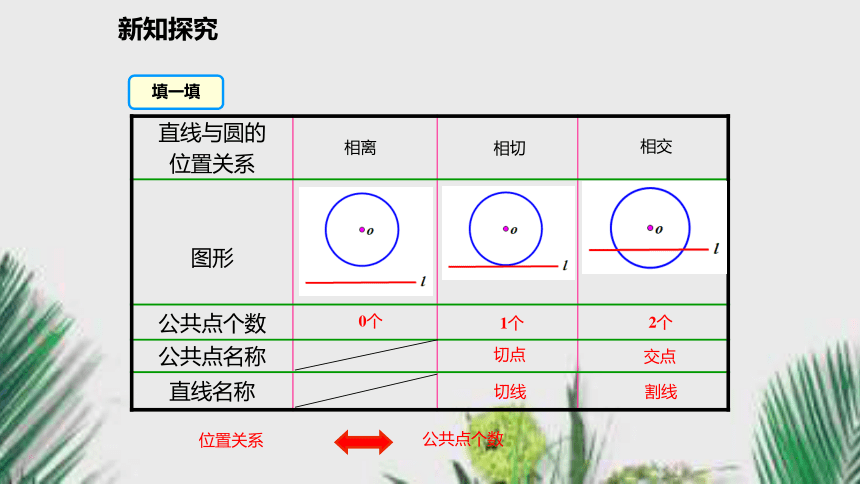
---摘自巴金《海上日出》新知探究互动探究问题1 如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?新知探究问题2 请同学在纸上画一条直线l,把硬币的边缘看作圆,在纸上移动硬币,你能发现直线和圆的公共点个数的变化情况吗?公共点个数最少时有几个?最多时有几个?●02●●新知探究2个交点割线1个切点切线0个相离相切相交位置关系公共点个数填一填新知探究直线与圆最多有两个公共点.
若直线与圆相交,则直线上的点都在圆上.
若A是☉O上一点,则直线AB与☉O相切.
④若C为☉O外一点,则过点C的直线与☉O相交或相离.
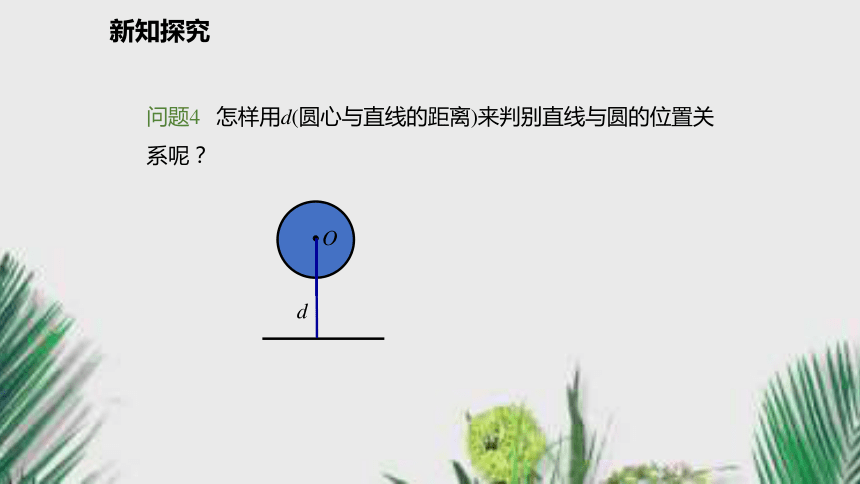
⑤直线a 和☉O有公共点,则直线a与☉O相交.√××××判一判新知探究问题3 刚才同学们在硬币靠近直线的移动过程中,除了发现公共点的个数发生了变化外,还发现有什么量也在改变?它与圆的半径有怎样的数量关系呢?圆心到直线的距离也在改变,在硬币逐渐靠近直线的时候,距离逐渐变小,在与圆有一个交点的时候距离跟半径相等,有两个交点时,距离小于半径,硬币离开直线的时候,距离大于半径.新知探究问题4 怎样用d(圆心与直线的距离)来判别直线与圆的位置关系呢?
Od新知探究直线和圆相交d< r直线和圆相切d= r直线和圆相离d> r数形结合:位置关系数量关系(用圆心O到直线的距离d与圆的半径r的关系来区分)ooo公共点个数直线与圆的位置关系
新知探究相交相切相离d > 5cmd = 5cm0cm≤ d < 5cm210新知探究例1 在Rt△ABC中,∠ACB=90°,AC=8,BC=6,以C为圆心,分别以下面给出的r为半径作圆,试问所作的圆与斜边AB所在的直线分别有怎样的位置关系?请说明理由.
(1) r=4; (2) r=4.8; (3) r=5.分析:要了解AB与☉C的位置关系,只要知道圆心C到AB的距离d与r的关系.已知r,只需求出C到AB的距离d.典例精析新知探究解:过C作CD⊥AB,垂足为D.在△ABC中,AB=10.根据三角形的面积公式有∴即圆心C到AB的距离d=4.8.所以 (1)当r=4时,有d >r,因此☉C和AB相离.d记住:斜边上的高等于两直角边的乘积除以斜边.新知探究 (2)当r=4.8时,有d=r.因此☉C和AB相切.d (3)当r=5时,有d1.直接根据定义,判断直线和圆的交点数;
2.判断圆心到直线的距离与半径r的大小关系.方法归纳新知探究例2 如图,Rt△ABC的斜边AB=10cm,∠A=30°.(1) 以点C为圆心,当半径为多少时,AB与☉C相切?(2) 以点C为圆心,半径r分别为4cm,5cm作两个圆,这两个圆与斜边AB分别有怎样的位置关系?解:(1) 过点C作边AB上的高CD.∵∠A=30°,AB=10cm,在Rt△BCD中,有课堂小结直线与圆的位置关系定义性质判定相离相切相交公共点的个数d与r的数量关系定义法性质法特别提醒:在图中没有d要先做出该垂线段相离:0个
相切:1个
相交:2个相离:d>r
相切:d=r
相交:dr:相离
d=r:相切
dA. r < 5 B. r > 5 C. r = 5 D. r ≥ 5
3. ☉O的最大弦长为8,若圆心O到直线l的距离为d=5,则直线l与☉O .
4. ☉O的半径为5,直线l上的一点到圆心O的距离是5,则直线l与☉O的位置关系是( )
A. 相交或相切 B. 相交或相离
C. 相切或相离 D. 上三种情况都有可能B相离A课堂小测解析:过点A作AQ⊥MN于Q,连接AN,设半径为r,由垂径定理有MQ=NQ,所以AQ=2,AN=r,NQ=4-r,利用勾股定理可以求出NQ=1.5,所以N点坐标为(-1,-2).5.如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M,N两点.若点M的坐标是(-4,-2),则点N的坐标为( )
A.(-1,-2) B.(1,2)
C.(-1.5,-2) D.(1.5,-2)Ax课堂小测拓展提升:
已知☉O的半径r=7cm,直线l1 // l2,且l1与☉O相切,圆心O到l2的距离为9cm.求l1与l2的距离.解:① l2与l1在圆的同一侧:
m=9-7=2 (cm);
②l2与l1在圆的两侧:
m=9+7=16 (cm).综上所述,l1与l2的距离为2cm或16cm.
2.能根据圆心到直线的距离d和圆的半径r之间的数量关系,
判断出直线与圆的位置关系.(重点)
复习导入情境引入太阳要从天边升起来了,便不转眼地望着那里. 果然过了一会儿,在那个地方出现了太阳的小半边脸,红是真红,却没有亮光.这个太阳好像负着重荷似地一步一步,慢慢地努力上升,到了最后,终于冲破了云霞,完全跳出了海面,颜色红得非常可爱.
---摘自巴金《海上日出》新知探究互动探究问题1 如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?新知探究问题2 请同学在纸上画一条直线l,把硬币的边缘看作圆,在纸上移动硬币,你能发现直线和圆的公共点个数的变化情况吗?公共点个数最少时有几个?最多时有几个?●02●●新知探究2个交点割线1个切点切线0个相离相切相交位置关系公共点个数填一填新知探究直线与圆最多有两个公共点.
若直线与圆相交,则直线上的点都在圆上.
若A是☉O上一点,则直线AB与☉O相切.
④若C为☉O外一点,则过点C的直线与☉O相交或相离.
⑤直线a 和☉O有公共点,则直线a与☉O相交.√××××判一判新知探究问题3 刚才同学们在硬币靠近直线的移动过程中,除了发现公共点的个数发生了变化外,还发现有什么量也在改变?它与圆的半径有怎样的数量关系呢?圆心到直线的距离也在改变,在硬币逐渐靠近直线的时候,距离逐渐变小,在与圆有一个交点的时候距离跟半径相等,有两个交点时,距离小于半径,硬币离开直线的时候,距离大于半径.新知探究问题4 怎样用d(圆心与直线的距离)来判别直线与圆的位置关系呢?
Od新知探究直线和圆相交d< r直线和圆相切d= r直线和圆相离d> r数形结合:位置关系数量关系(用圆心O到直线的距离d与圆的半径r的关系来区分)ooo公共点个数直线与圆的位置关系
新知探究相交相切相离d > 5cmd = 5cm0cm≤ d < 5cm210新知探究例1 在Rt△ABC中,∠ACB=90°,AC=8,BC=6,以C为圆心,分别以下面给出的r为半径作圆,试问所作的圆与斜边AB所在的直线分别有怎样的位置关系?请说明理由.
(1) r=4; (2) r=4.8; (3) r=5.分析:要了解AB与☉C的位置关系,只要知道圆心C到AB的距离d与r的关系.已知r,只需求出C到AB的距离d.典例精析新知探究解:过C作CD⊥AB,垂足为D.在△ABC中,AB=10.根据三角形的面积公式有∴即圆心C到AB的距离d=4.8.所以 (1)当r=4时,有d >r,因此☉C和AB相离.d记住:斜边上的高等于两直角边的乘积除以斜边.新知探究 (2)当r=4.8时,有d=r.因此☉C和AB相切.d (3)当r=5时,有d
2.判断圆心到直线的距离与半径r的大小关系.方法归纳新知探究例2 如图,Rt△ABC的斜边AB=10cm,∠A=30°.(1) 以点C为圆心,当半径为多少时,AB与☉C相切?(2) 以点C为圆心,半径r分别为4cm,5cm作两个圆,这两个圆与斜边AB分别有怎样的位置关系?解:(1) 过点C作边AB上的高CD.∵∠A=30°,AB=10cm,在Rt△BCD中,有课堂小结直线与圆的位置关系定义性质判定相离相切相交公共点的个数d与r的数量关系定义法性质法特别提醒:在图中没有d要先做出该垂线段相离:0个
相切:1个
相交:2个相离:d>r
相切:d=r
相交:d
d=r:相切
d
3. ☉O的最大弦长为8,若圆心O到直线l的距离为d=5,则直线l与☉O .
4. ☉O的半径为5,直线l上的一点到圆心O的距离是5,则直线l与☉O的位置关系是( )
A. 相交或相切 B. 相交或相离
C. 相切或相离 D. 上三种情况都有可能B相离A课堂小测解析:过点A作AQ⊥MN于Q,连接AN,设半径为r,由垂径定理有MQ=NQ,所以AQ=2,AN=r,NQ=4-r,利用勾股定理可以求出NQ=1.5,所以N点坐标为(-1,-2).5.如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M,N两点.若点M的坐标是(-4,-2),则点N的坐标为( )
A.(-1,-2) B.(1,2)
C.(-1.5,-2) D.(1.5,-2)Ax课堂小测拓展提升:
已知☉O的半径r=7cm,直线l1 // l2,且l1与☉O相切,圆心O到l2的距离为9cm.求l1与l2的距离.解:① l2与l1在圆的同一侧:
m=9-7=2 (cm);
②l2与l1在圆的两侧:
m=9+7=16 (cm).综上所述,l1与l2的距离为2cm或16cm.
