1.2.2同角三角函数的基本关系(共37张PPT)
文档属性
| 名称 | 1.2.2同角三角函数的基本关系(共37张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 11:00:25 | ||
图片预览











文档简介
(共37张PPT)
1.2.2 同角三角函数的基本关系
问题1:回顾三角函数的定义。
设置目的:温故知新,三角函数定义是推导关系式的基础理论。
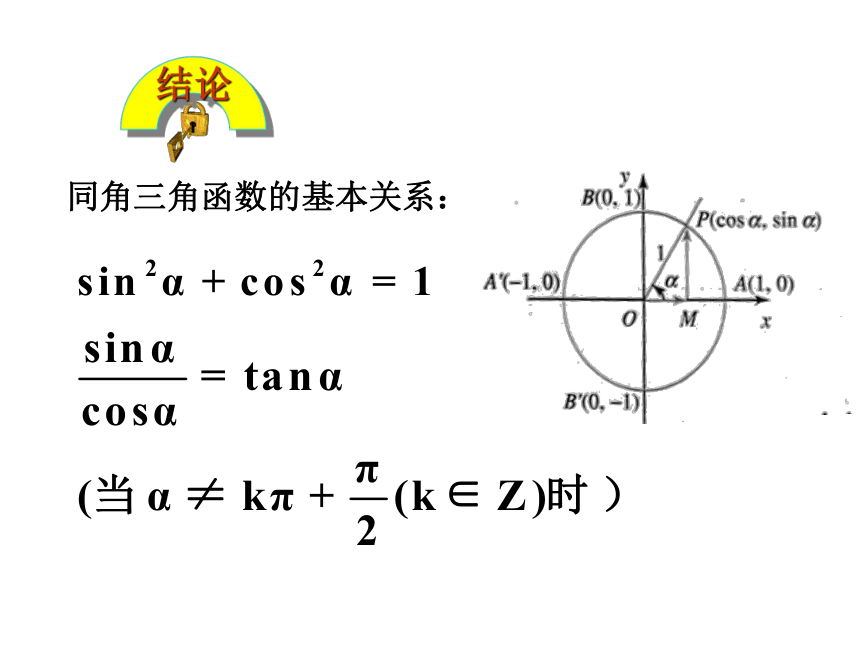
问题2:角α终边与单位圆的交点P的坐标是什么?
设置目的:单位圆中推导公式会用到P点的坐标,P的坐标是此处数与形的交汇点。
由三角函数定义我们可以看到:
同角三角函数的基本关系:
用文字叙述:
同一个角α的正弦、余弦的平方和等于1,商等于角α的正切;同一个角的正切、余切之积等于1(即同一个角的正切、余切互为倒数)。
为了加深对关系式的认识,在公式给出后设置了几点注意 :
1、同角的理解:
2、对“任意”一个角(在使函数有意义的前提下)关系式都成立。
3、 是 的简写形式,与 不同.
4、公式可以变形使用
已知 ,且 是第二象限角,
求 , 的值。
解:
从而 .
例1:
因为sinα2+cosα2=1,所以
解:
为什么?
例2:
1、已知一个角的某一个三角函数值,便可运用基本关系式求出其它三角函数值.在求值中,确定角的终边位置是关键和必要的.有时,由于角的终边位置的不确定,因此解的情况不止一种。
2、解题时产生遗漏的主要原因是:①没有确定好或不去确定角的终边位置;②利用平方关系开平方时,漏掉了负的平方根。
求证:
例3
所以原式成立。
且
所以原式成立。
证法2:
因为
解:
3、利用平方关系时,往往要开方,因此要先
根据角所在象限确定符号,即要就角所在
象限进行分类讨论。
(2017宁夏)若 ,则 的值为( )
C
解析:
有已知得:
∴
D
解析:
本题考查同角三角函数关系及求值问题
所求式
3(2017陕西)已知sinα= 则sin4α-cos4α的值为( )
B.
C. D.
A
解析:
B
B
3、若
,则
的值为_____
4、已知
则m=_________;
__________.
0或8
,
已知 ,求
∵
∴
又∵
∴α在第二或三象限角。
解:
5、
α在第二象限时,即有
从而
当
α在第四象限时,即有
从而
当
∴
∴
已知
并且α是第二象限角,
求
∵
∴
又∵
α是第二象限角,
即有
从而
∴
解:
6、
,
,
7、已知
,求
的值。
由
可得:
解:
于是:
∴
1、
2、当 为第二象限角时,
当 为第四象限角时,
3、当 为第一象限角时,
当 为第二象限角时,
4、(1) (2)1
5、(1)
(2)
1.2.2 同角三角函数的基本关系
问题1:回顾三角函数的定义。
设置目的:温故知新,三角函数定义是推导关系式的基础理论。
问题2:角α终边与单位圆的交点P的坐标是什么?
设置目的:单位圆中推导公式会用到P点的坐标,P的坐标是此处数与形的交汇点。
由三角函数定义我们可以看到:
同角三角函数的基本关系:
用文字叙述:
同一个角α的正弦、余弦的平方和等于1,商等于角α的正切;同一个角的正切、余切之积等于1(即同一个角的正切、余切互为倒数)。
为了加深对关系式的认识,在公式给出后设置了几点注意 :
1、同角的理解:
2、对“任意”一个角(在使函数有意义的前提下)关系式都成立。
3、 是 的简写形式,与 不同.
4、公式可以变形使用
已知 ,且 是第二象限角,
求 , 的值。
解:
从而 .
例1:
因为sinα2+cosα2=1,所以
解:
为什么?
例2:
1、已知一个角的某一个三角函数值,便可运用基本关系式求出其它三角函数值.在求值中,确定角的终边位置是关键和必要的.有时,由于角的终边位置的不确定,因此解的情况不止一种。
2、解题时产生遗漏的主要原因是:①没有确定好或不去确定角的终边位置;②利用平方关系开平方时,漏掉了负的平方根。
求证:
例3
所以原式成立。
且
所以原式成立。
证法2:
因为
解:
3、利用平方关系时,往往要开方,因此要先
根据角所在象限确定符号,即要就角所在
象限进行分类讨论。
(2017宁夏)若 ,则 的值为( )
C
解析:
有已知得:
∴
D
解析:
本题考查同角三角函数关系及求值问题
所求式
3(2017陕西)已知sinα= 则sin4α-cos4α的值为( )
B.
C. D.
A
解析:
B
B
3、若
,则
的值为_____
4、已知
则m=_________;
__________.
0或8
,
已知 ,求
∵
∴
又∵
∴α在第二或三象限角。
解:
5、
α在第二象限时,即有
从而
当
α在第四象限时,即有
从而
当
∴
∴
已知
并且α是第二象限角,
求
∵
∴
又∵
α是第二象限角,
即有
从而
∴
解:
6、
,
,
7、已知
,求
的值。
由
可得:
解:
于是:
∴
1、
2、当 为第二象限角时,
当 为第四象限角时,
3、当 为第一象限角时,
当 为第二象限角时,
4、(1) (2)1
5、(1)
(2)
