沪科版九年级数学下册 24.4.3切线长定理 课件(共22张PPT)
文档属性
| 名称 | 沪科版九年级数学下册 24.4.3切线长定理 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-07 12:12:31 | ||
图片预览



文档简介
课件22张PPT。第二十四章
圆九年级数学沪科版·下册24.4.3切线长定理教学目标1.掌握切线长的定义及切线长定理.(重点)
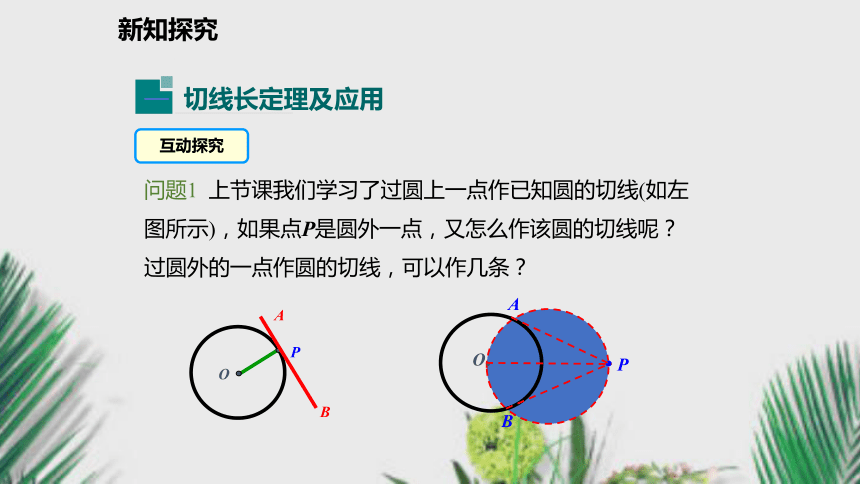
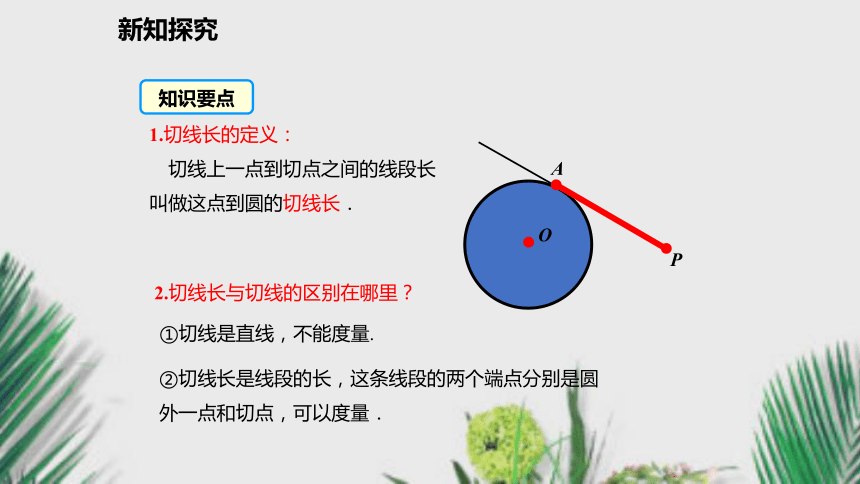
2.初步学会运用切线长定理进行计算与证明.(难点)复习导入情境引入同学们玩过空竹和悠悠球吗?在空竹和悠悠球的旋转的那一瞬间,你能从中抽象出什么样数学图形?新知探究互动探究问题1 上节课我们学习了过圆上一点作已知圆的切线(如左图所示),如果点P是圆外一点,又怎么作该圆的切线呢?过圆外的一点作圆的切线,可以作几条?A B 新知探究1.切线长的定义:
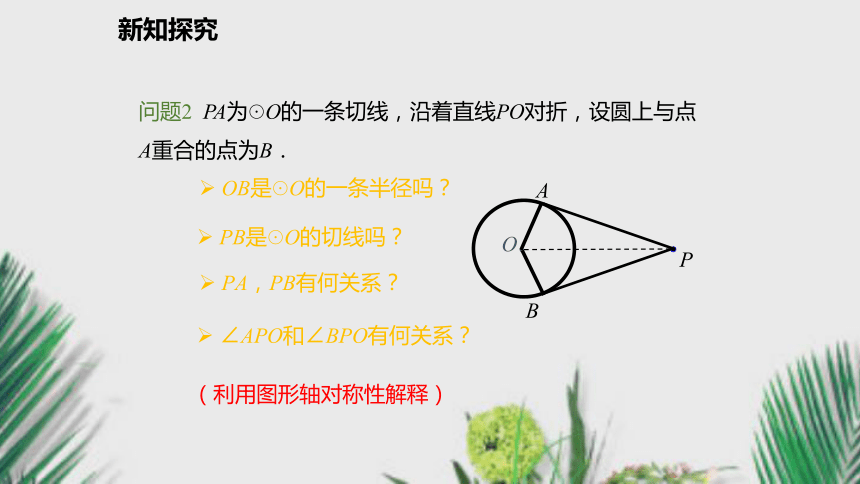
切线上一点到切点之间的线段长叫做这点到圆的切线长.AO①切线是直线,不能度量.②切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.2.切线长与切线的区别在哪里?知识要点新知探究问题2 PA为☉O的一条切线,沿着直线PO对折,设圆上与点A重合的点为B. OB是☉O的一条半径吗? PB是☉O的切线吗?(利用图形轴对称性解释) PA,PB有何关系? ∠APO和∠BPO有何关系?新知探究BPOA切线长定理:
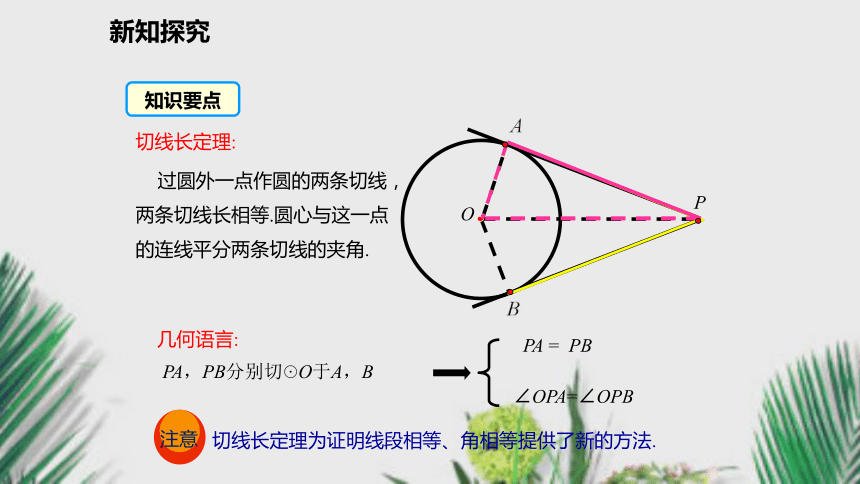
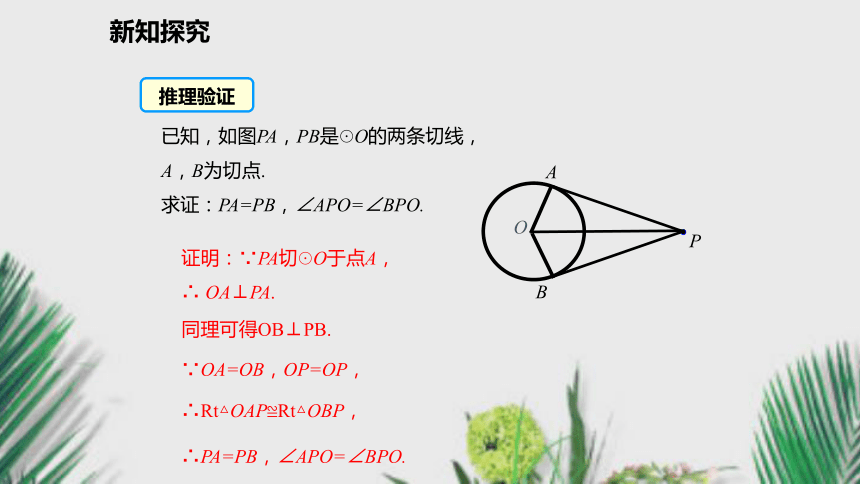
过圆外一点作圆的两条切线,两条切线长相等.圆心与这一点的连线平分两条切线的夹角.PA,PB分别切☉O于A,BPA = PB∠OPA=∠OPB几何语言: 切线长定理为证明线段相等、角相等提供了新的方法.知识要点新知探究已知,如图PA,PB是☉O的两条切线,A,B为切点.
求证:PA=PB,∠APO=∠BPO.证明:∵PA切☉O于点A,
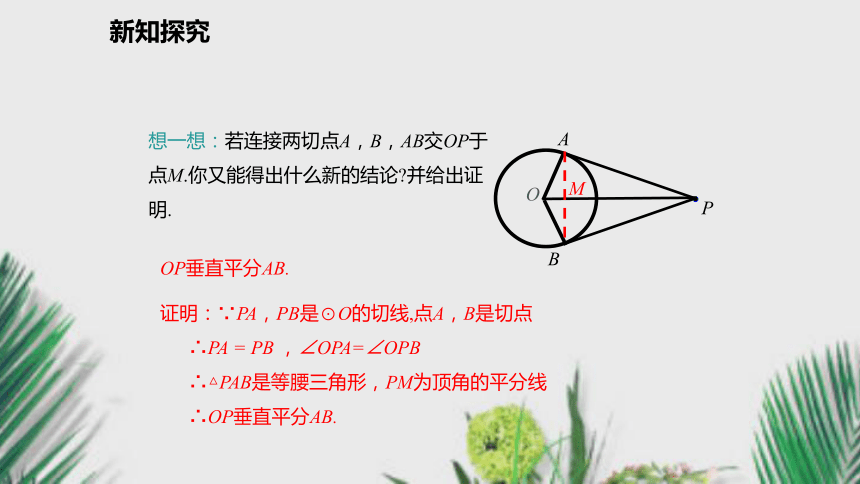
∴ OA⊥PA.同理可得OB⊥PB.∵OA=OB,OP=OP,∴Rt△OAP≌Rt△OBP,∴PA=PB,∠APO=∠BPO.推理验证新知探究想一想:若连接两切点A,B,AB交OP于点M.你又能得出什么新的结论?并给出证明.OP垂直平分AB.证明:∵PA,PB是⊙O的切线,点A,B是切点
∴PA = PB ,∠OPA=∠OPB
∴△PAB是等腰三角形,PM为顶角的平分线
∴OP垂直平分AB.M新知探究想一想:若延长PO交⊙O于点C,连接CA,CB,你又能得出什么新的结论?请给出证明.证明:∵PA,PB是⊙O的切线,点A,B是切点,
∴PA = PB ,∠OPA=∠OPB.
PC=PC.
∴ △PCA ≌ △PCB,
∴AC=BC.AC=BCC新知探究典例精析例1 已知:如图,四边形ABCD的边AB,BC,CD,
DA与⊙O分别相切于点E,F,G,H.求证:AB+CD=DA+BC.O证明:∵AB,BC,CD,DA与⊙O相切,E,F,G,H是切点,EFGH∴ AE=AH,BE=BF,CG=CF,DG=DH.∴ AE+BE+CG+DG=AH+BF+CF+DH,即AB+CD=DA+BC.新知探究例2 为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径.若三角板与圆相切且测得PA=5cm,求铁环的半径.解析:欲求半径OP,取圆的圆心为O,连OA,OP,由切线性质知△OPA为直角三角形,从而在Rt△OPA中由勾股定理易求得半径.BC新知探究在Rt△OPA中,PA=5,∠POA=30°,Q解:过O作OQ⊥AB于Q,设铁环的圆心为O,连接OP,OA.∵AP,AQ为⊙O的切线,∴AO为∠PAQ的平分线,即∠PAO=∠QAO.又∠BAC=60°,∠PAO+∠QAO+∠BAC=180°,∴∠PAO=∠QAO=60°.BC∴新知探究1.PA,PB是☉O的两条切线,A,B为切点,直线OP交☉O于点D,E,交AB于C.(1)写出图中所有的垂直关系;OA⊥PA,OB ⊥PB,AB ⊥OP.(3)写出图中所有的全等三角形;△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP.(4)写出图中所有的等腰三角形.△ABP △AOB(2)写出图中与∠OAC相等的角;∠OAC=∠OBC=∠APC=∠BPC.练一练新知探究 2.PA,PB是☉O的两条切线,A,B是切点,OA=3.(1)若AP=4,则OP= ;(2)若∠BPA=60 °,则OP= .56新知探究解:⑴连接OA,OB,OC,OD和OE.
∵PA,PB是☉O的两条切线,点A,B是切点,
∴PA=PB=7.
又∵DC,DA是☉O的两条切线,点C,A是切点,
∴DC=DA.同理可得CE=EB.
新知探究⑵∵D,E是切线PA,PB上的点,
∠PAO=∠PBO=90°,
∴∠AOB=360°-∠PAO-∠PBO-∠P=140°.
∴S△PDE=PD+DE+PE=PD+DC+CE+PE=PA+PB=14.新知探究切线长问题辅助线添加方法:
(1)分别连接圆心和切点;
(2)连接两切点;
(3)连接圆心和圆外一点.方法归纳课堂小结切线长切线长定理作用图形的轴对称性原理提供了证线段和
角相等的新方法辅助线分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.课堂小测20 ° 4120 ° 课堂小测3.如图所示,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC相切于点D.
求证:DE∥OC.方法一:
证明:连接OD.
∵AC切⊙O于点D,∴OD⊥AC,
∴∠ODC=∠B=90°.
在Rt△OCD和Rt△OCB中,
OD=OB ,OC=OC
∴Rt△ODC≌Rt△OBC(HL),
∴∠DOC=∠BOC.
∵OD=OE,∴∠ODE=∠OED.
∵∠DOB=∠ODE+∠OED,
∴∠BOC=∠OED,∴DE∥OC.课堂小测方法二:
证明:连接BD.
∵AC切⊙O于点D,BC切⊙O于点B,∴DC=BC,OC平分∠DCB.
∴OC⊥BD.
∵BE为⊙O的直径,∴DE⊥BD.
∴DE∥OC.
2.初步学会运用切线长定理进行计算与证明.(难点)复习导入情境引入同学们玩过空竹和悠悠球吗?在空竹和悠悠球的旋转的那一瞬间,你能从中抽象出什么样数学图形?新知探究互动探究问题1 上节课我们学习了过圆上一点作已知圆的切线(如左图所示),如果点P是圆外一点,又怎么作该圆的切线呢?过圆外的一点作圆的切线,可以作几条?A B 新知探究1.切线长的定义:
切线上一点到切点之间的线段长叫做这点到圆的切线长.AO①切线是直线,不能度量.②切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.2.切线长与切线的区别在哪里?知识要点新知探究问题2 PA为☉O的一条切线,沿着直线PO对折,设圆上与点A重合的点为B. OB是☉O的一条半径吗? PB是☉O的切线吗?(利用图形轴对称性解释) PA,PB有何关系? ∠APO和∠BPO有何关系?新知探究BPOA切线长定理:
过圆外一点作圆的两条切线,两条切线长相等.圆心与这一点的连线平分两条切线的夹角.PA,PB分别切☉O于A,BPA = PB∠OPA=∠OPB几何语言: 切线长定理为证明线段相等、角相等提供了新的方法.知识要点新知探究已知,如图PA,PB是☉O的两条切线,A,B为切点.
求证:PA=PB,∠APO=∠BPO.证明:∵PA切☉O于点A,
∴ OA⊥PA.同理可得OB⊥PB.∵OA=OB,OP=OP,∴Rt△OAP≌Rt△OBP,∴PA=PB,∠APO=∠BPO.推理验证新知探究想一想:若连接两切点A,B,AB交OP于点M.你又能得出什么新的结论?并给出证明.OP垂直平分AB.证明:∵PA,PB是⊙O的切线,点A,B是切点
∴PA = PB ,∠OPA=∠OPB
∴△PAB是等腰三角形,PM为顶角的平分线
∴OP垂直平分AB.M新知探究想一想:若延长PO交⊙O于点C,连接CA,CB,你又能得出什么新的结论?请给出证明.证明:∵PA,PB是⊙O的切线,点A,B是切点,
∴PA = PB ,∠OPA=∠OPB.
PC=PC.
∴ △PCA ≌ △PCB,
∴AC=BC.AC=BCC新知探究典例精析例1 已知:如图,四边形ABCD的边AB,BC,CD,
DA与⊙O分别相切于点E,F,G,H.求证:AB+CD=DA+BC.O证明:∵AB,BC,CD,DA与⊙O相切,E,F,G,H是切点,EFGH∴ AE=AH,BE=BF,CG=CF,DG=DH.∴ AE+BE+CG+DG=AH+BF+CF+DH,即AB+CD=DA+BC.新知探究例2 为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径.若三角板与圆相切且测得PA=5cm,求铁环的半径.解析:欲求半径OP,取圆的圆心为O,连OA,OP,由切线性质知△OPA为直角三角形,从而在Rt△OPA中由勾股定理易求得半径.BC新知探究在Rt△OPA中,PA=5,∠POA=30°,Q解:过O作OQ⊥AB于Q,设铁环的圆心为O,连接OP,OA.∵AP,AQ为⊙O的切线,∴AO为∠PAQ的平分线,即∠PAO=∠QAO.又∠BAC=60°,∠PAO+∠QAO+∠BAC=180°,∴∠PAO=∠QAO=60°.BC∴新知探究1.PA,PB是☉O的两条切线,A,B为切点,直线OP交☉O于点D,E,交AB于C.(1)写出图中所有的垂直关系;OA⊥PA,OB ⊥PB,AB ⊥OP.(3)写出图中所有的全等三角形;△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP.(4)写出图中所有的等腰三角形.△ABP △AOB(2)写出图中与∠OAC相等的角;∠OAC=∠OBC=∠APC=∠BPC.练一练新知探究 2.PA,PB是☉O的两条切线,A,B是切点,OA=3.(1)若AP=4,则OP= ;(2)若∠BPA=60 °,则OP= .56新知探究解:⑴连接OA,OB,OC,OD和OE.
∵PA,PB是☉O的两条切线,点A,B是切点,
∴PA=PB=7.
又∵DC,DA是☉O的两条切线,点C,A是切点,
∴DC=DA.同理可得CE=EB.
新知探究⑵∵D,E是切线PA,PB上的点,
∠PAO=∠PBO=90°,
∴∠AOB=360°-∠PAO-∠PBO-∠P=140°.
∴S△PDE=PD+DE+PE=PD+DC+CE+PE=PA+PB=14.新知探究切线长问题辅助线添加方法:
(1)分别连接圆心和切点;
(2)连接两切点;
(3)连接圆心和圆外一点.方法归纳课堂小结切线长切线长定理作用图形的轴对称性原理提供了证线段和
角相等的新方法辅助线分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.课堂小测20 ° 4120 ° 课堂小测3.如图所示,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC相切于点D.
求证:DE∥OC.方法一:
证明:连接OD.
∵AC切⊙O于点D,∴OD⊥AC,
∴∠ODC=∠B=90°.
在Rt△OCD和Rt△OCB中,
OD=OB ,OC=OC
∴Rt△ODC≌Rt△OBC(HL),
∴∠DOC=∠BOC.
∵OD=OE,∴∠ODE=∠OED.
∵∠DOB=∠ODE+∠OED,
∴∠BOC=∠OED,∴DE∥OC.课堂小测方法二:
证明:连接BD.
∵AC切⊙O于点D,BC切⊙O于点B,∴DC=BC,OC平分∠DCB.
∴OC⊥BD.
∵BE为⊙O的直径,∴DE⊥BD.
∴DE∥OC.
