1.3三角函数的诱导公式(共38张PPT)
文档属性
| 名称 | 1.3三角函数的诱导公式(共38张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 11:02:20 | ||
图片预览





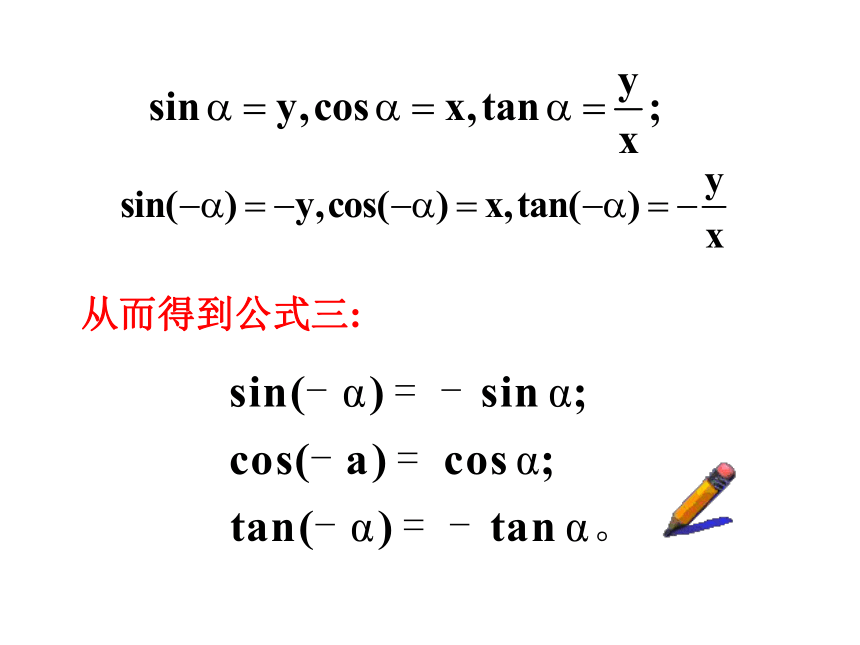


文档简介
(共38张PPT)
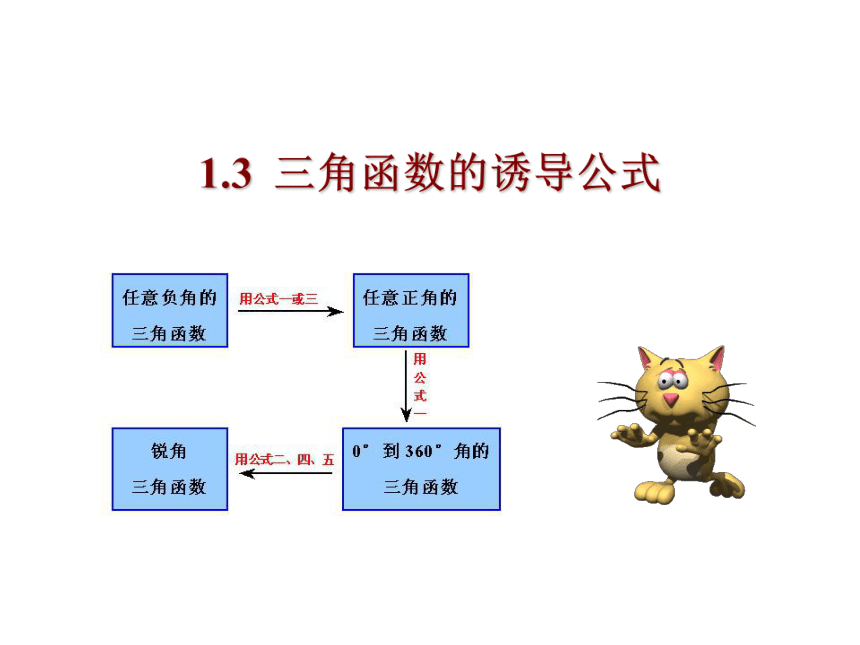
1.3 三角函数的诱导公式
能否把 任意角的三角函数求值,化为我们熟悉的0°~360°间的角的三角函数求值问题呢?
诱导公式 一:
能否再把0°~360°间的角的三角函数求值,化为我们熟悉的0°~90°间的角的三角函数求值问题呢?
如果能的话,那么任意角的三角函数求值,都可以化归为锐角三角函数求值,并通过求锐角三角函数方法而得到最终解决,本课就来讨论这一问题。
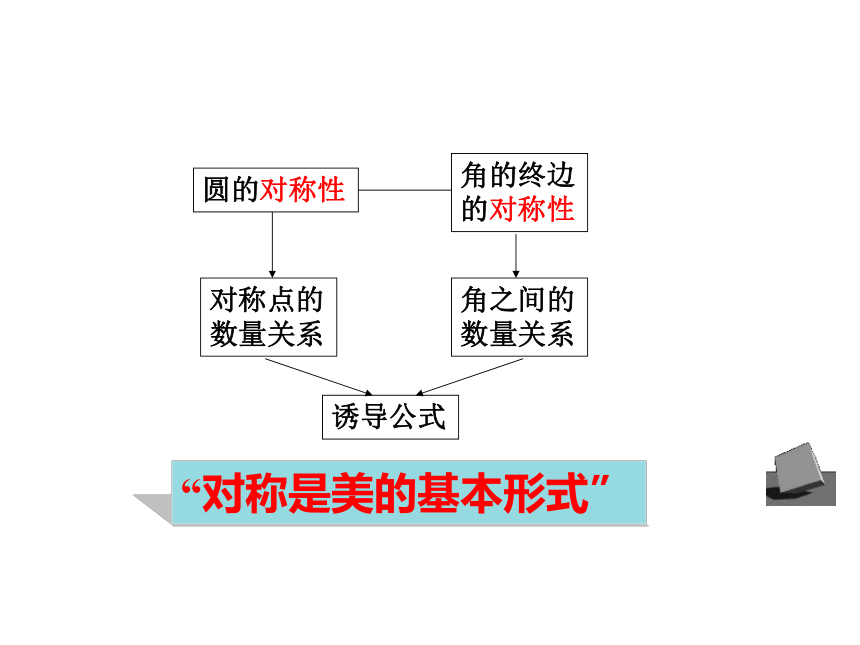
“对称是美的基本形式”
设 0°≤α≤90°,对于任意一个 0°到360°的角β,以下四种情形中有且仅有一种成立。
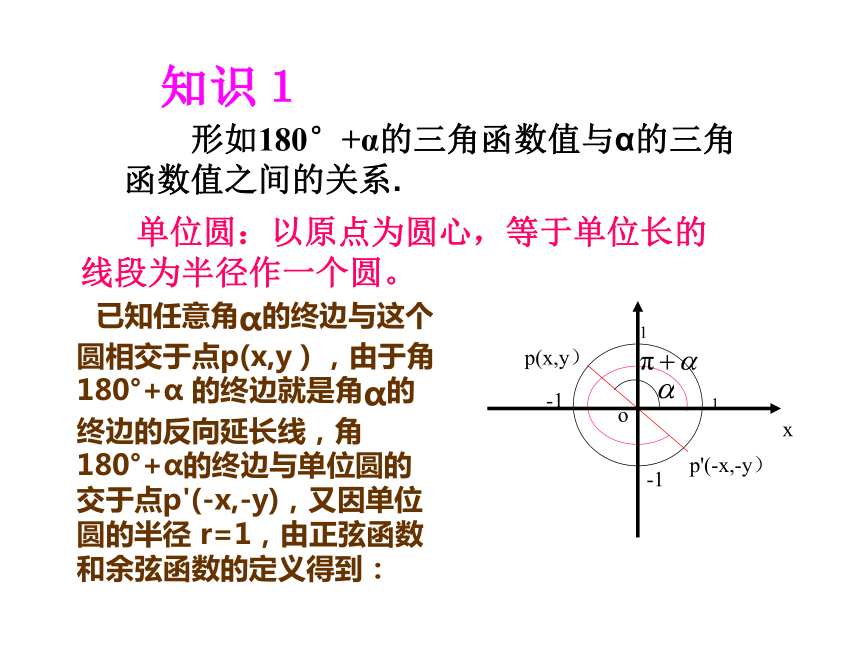
形如180°+α的三角函数值与α的三角函数值之间的关系.
单位圆:以原点为圆心,等于单位长的线段为半径作一个圆。
已知任意角α的终边与这个圆相交于点p(x,y),由于角 180°+α 的终边就是角α的终边的反向延长线,角180°+α的终边与单位圆的交于点p'(-x,-y),又因单位圆的半径 r=1,由正弦函数和余弦函数的定义得到:
从而得到公式二:
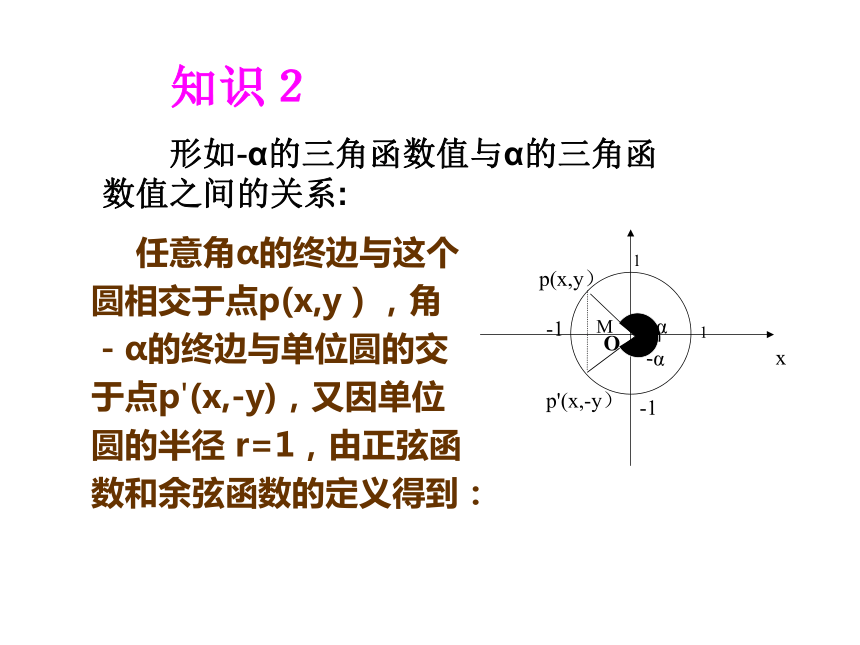
形如-α的三角函数值与α的三角函数值之间的关系:
任意角α的终边与这个圆相交于点p(x,y),角-α的终边与单位圆的交于点p'(x,-y),又因单位圆的半径 r=1,由正弦函数和余弦函数的定义得到:
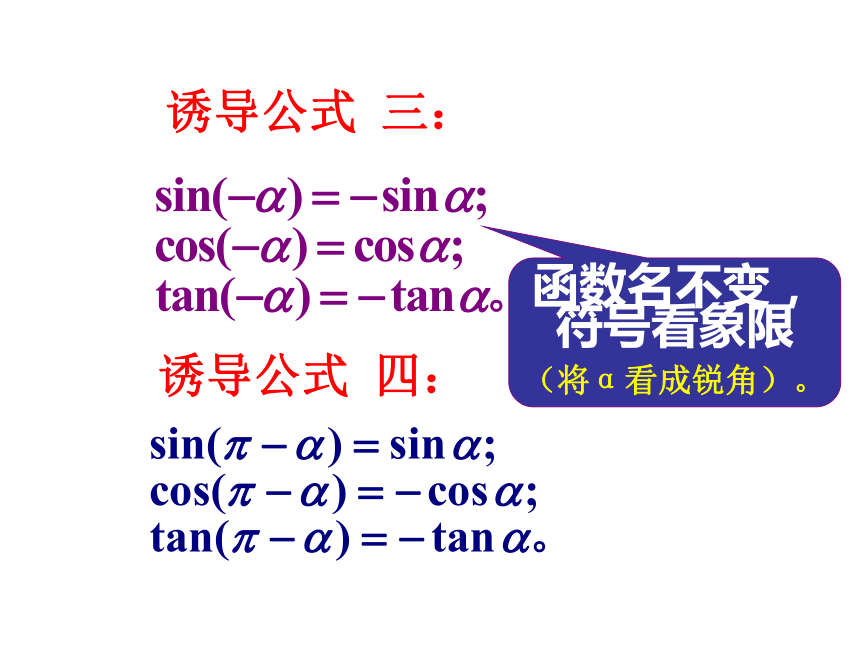
从而得到公式三:
同理可得公式四:
诱导公式 一:
函数名不变,符号看象限
(将α看成锐角)。
诱导公式 二:
诱导公式 四:
函数名不变,符号看象限
(将α看成锐角)。
诱导公式 三:
公式一、二、三、四都叫做诱导公式.
简化成“函数名不变,符号看象限”的口诀。
例1:将下列各三角函数化成锐角三角函数。
(1) sin(-699? ) (2) cos(-1525? )
(3) tan(-872? )
答案:(1) –sin21? (2) cos85?
(3) tan28?
解:⑴
⑵
⑶
例3:已知 如何求
y
利用诱导公式把任意角的三角函数转化为锐角三角函数,一般按下面步骤进行:
任意负角的
三角函数
任意正角的
三角函数
锐角三
角函数
解:
从而得公式五:
同样可得公式六:
诱导公式五:
诱导公式六:
函数名变余,符号看象限
(将α看成锐角)
综上:奇变偶不变,符号看象限.
求sinθ,cosθ,tanθ时,把θ化成θ=k· +α,则
k为奇数时,函数名变为其余函数,k为偶数时函数名不变;
符号由将α看成锐角时,θ所在象限的原来函数决定。
口诀:奇变偶不变,符号看象限.
意义:
例5:
解:
利用公式求下列各三角函数值.
(1) (2)
例6:
解:
(1)
(2)
解:
公式一、二、三、四都叫做诱导公式.
简化成“函数名不变,符号看象限”的口诀。
公式五、公式六概括如下:
简化成“奇变偶不变,符号看象限”的口诀。
C
解析:
A
2、填空:
(2)
答案:(1)0; (2)0.
(1)tan675°+tan765°-tan(-330°)+tan(-690°)____________.
3、化简
1.3 三角函数的诱导公式
能否把 任意角的三角函数求值,化为我们熟悉的0°~360°间的角的三角函数求值问题呢?
诱导公式 一:
能否再把0°~360°间的角的三角函数求值,化为我们熟悉的0°~90°间的角的三角函数求值问题呢?
如果能的话,那么任意角的三角函数求值,都可以化归为锐角三角函数求值,并通过求锐角三角函数方法而得到最终解决,本课就来讨论这一问题。
“对称是美的基本形式”
设 0°≤α≤90°,对于任意一个 0°到360°的角β,以下四种情形中有且仅有一种成立。
形如180°+α的三角函数值与α的三角函数值之间的关系.
单位圆:以原点为圆心,等于单位长的线段为半径作一个圆。
已知任意角α的终边与这个圆相交于点p(x,y),由于角 180°+α 的终边就是角α的终边的反向延长线,角180°+α的终边与单位圆的交于点p'(-x,-y),又因单位圆的半径 r=1,由正弦函数和余弦函数的定义得到:
从而得到公式二:
形如-α的三角函数值与α的三角函数值之间的关系:
任意角α的终边与这个圆相交于点p(x,y),角-α的终边与单位圆的交于点p'(x,-y),又因单位圆的半径 r=1,由正弦函数和余弦函数的定义得到:
从而得到公式三:
同理可得公式四:
诱导公式 一:
函数名不变,符号看象限
(将α看成锐角)。
诱导公式 二:
诱导公式 四:
函数名不变,符号看象限
(将α看成锐角)。
诱导公式 三:
公式一、二、三、四都叫做诱导公式.
简化成“函数名不变,符号看象限”的口诀。
例1:将下列各三角函数化成锐角三角函数。
(1) sin(-699? ) (2) cos(-1525? )
(3) tan(-872? )
答案:(1) –sin21? (2) cos85?
(3) tan28?
解:⑴
⑵
⑶
例3:已知 如何求
y
利用诱导公式把任意角的三角函数转化为锐角三角函数,一般按下面步骤进行:
任意负角的
三角函数
任意正角的
三角函数
锐角三
角函数
解:
从而得公式五:
同样可得公式六:
诱导公式五:
诱导公式六:
函数名变余,符号看象限
(将α看成锐角)
综上:奇变偶不变,符号看象限.
求sinθ,cosθ,tanθ时,把θ化成θ=k· +α,则
k为奇数时,函数名变为其余函数,k为偶数时函数名不变;
符号由将α看成锐角时,θ所在象限的原来函数决定。
口诀:奇变偶不变,符号看象限.
意义:
例5:
解:
利用公式求下列各三角函数值.
(1) (2)
例6:
解:
(1)
(2)
解:
公式一、二、三、四都叫做诱导公式.
简化成“函数名不变,符号看象限”的口诀。
公式五、公式六概括如下:
简化成“奇变偶不变,符号看象限”的口诀。
C
解析:
A
2、填空:
(2)
答案:(1)0; (2)0.
(1)tan675°+tan765°-tan(-330°)+tan(-690°)____________.
3、化简
