1.4.2正、余弦函数的性质(共51张PPT)
文档属性
| 名称 | 1.4.2正、余弦函数的性质(共51张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 11:04:37 | ||
图片预览






文档简介
(共51张PPT)
正弦函数的图像
余弦函数的图像
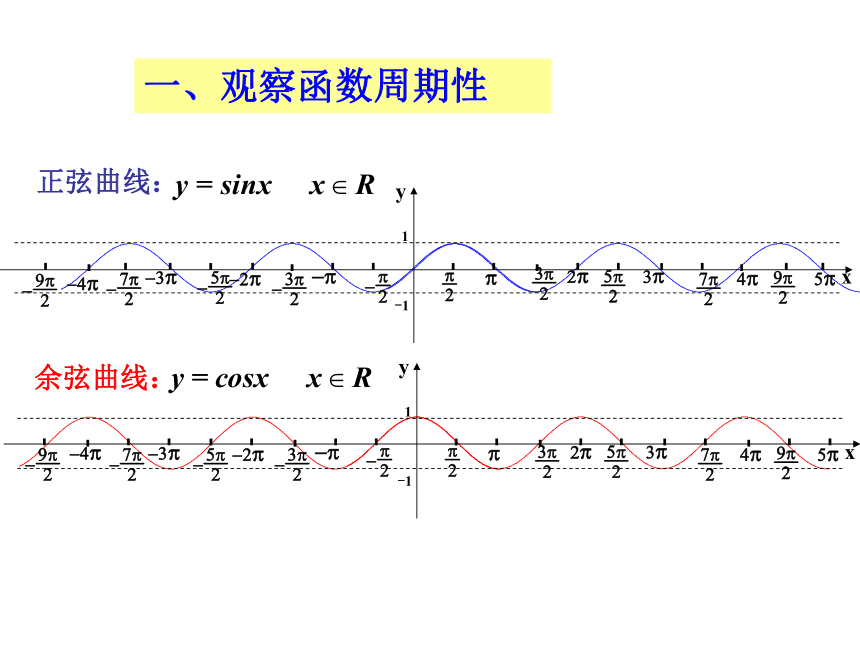
一、观察函数周期性
周期函数定义:对于函数f (x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有
f (x+T)=f (x)
那么,函数f (x)就叫做周期函数,非零常数T叫做这个函数的周期。
1、T是非零常数;
2、“每一个值”只要有一个反例,则f (x)就不为周期函数(如f (x0+t)?f (x0));
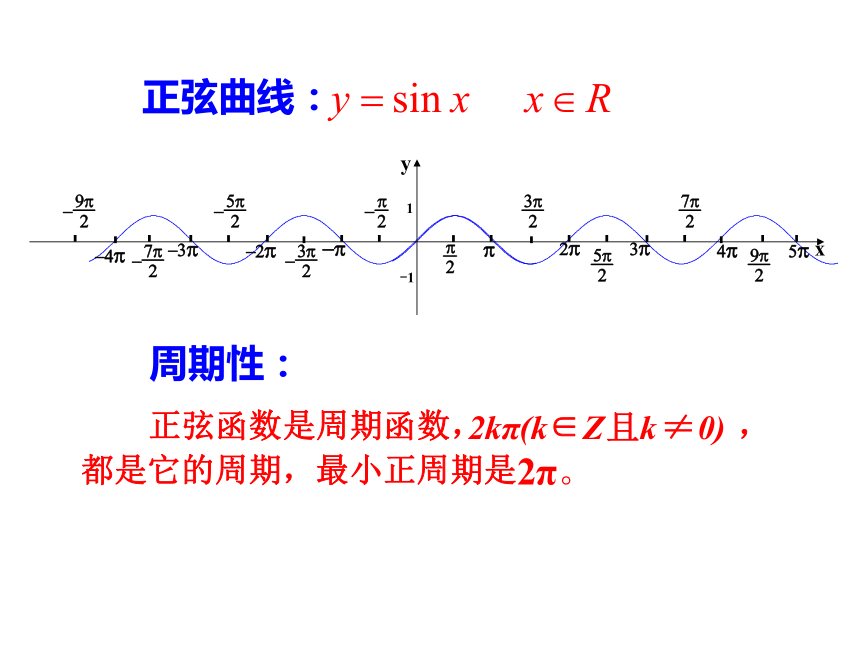
3、周期函数的周期T往往是多值的(如y=sinx,2?,4?,…,-2?,-4?,…都是它的周期);
4、周期T中最小的正数叫做f (x)的最小正周期(有些周期函数没有最小正周期).
正弦曲线:
周期性:
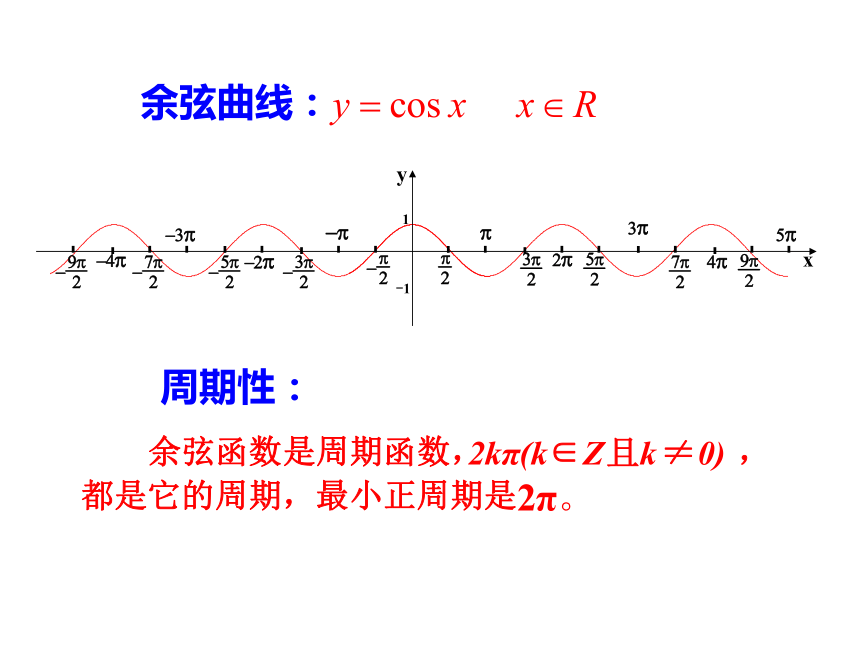
周期性:
余弦曲线:
例1.求下列函数的周期.
(2) ∵
解:
注:由上面的得出:
正弦函数的图像
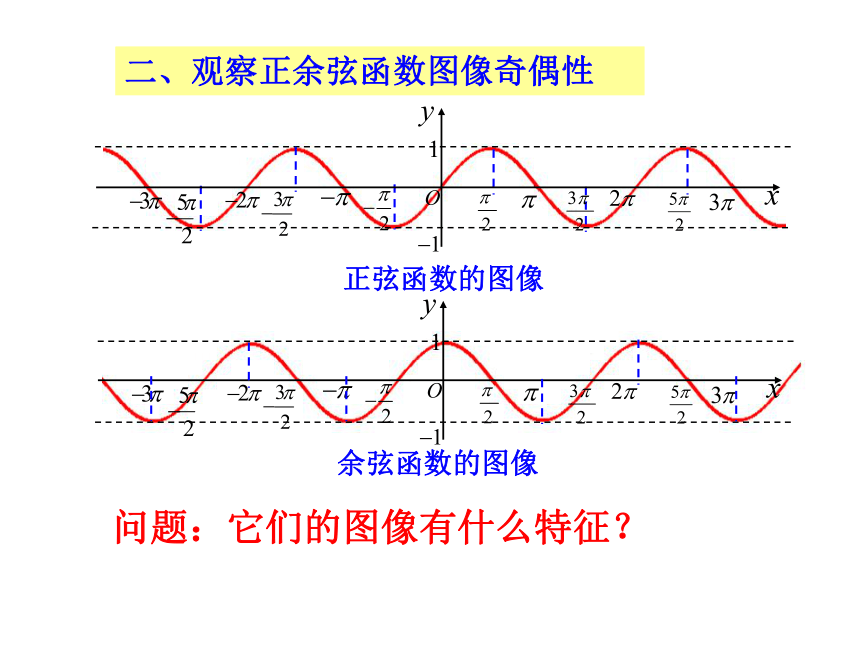
二、观察正余弦函数图像奇偶性
余弦函数的图像
问题:它们的图像有什么特征?
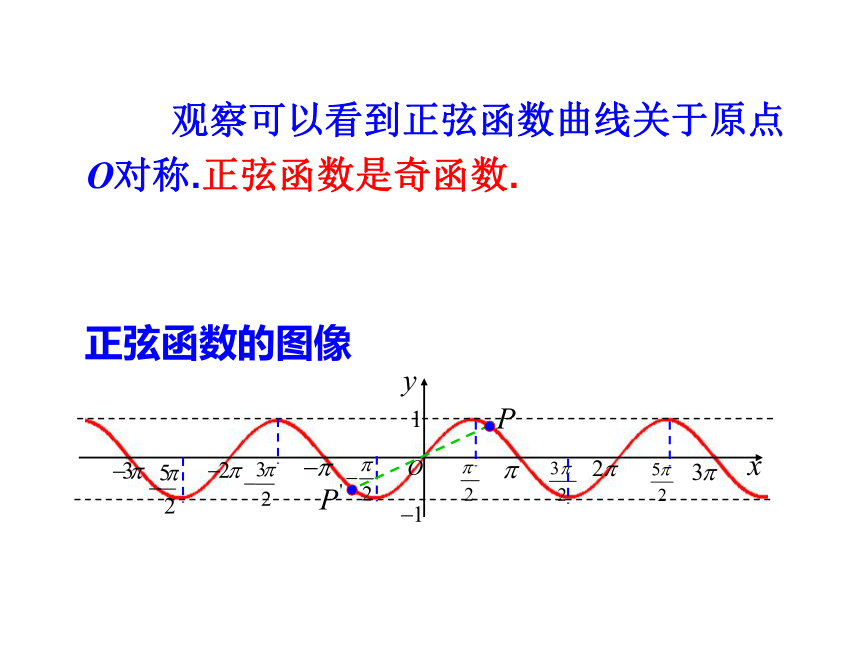
观察可以看到正弦函数曲线关于原点O对称.正弦函数是奇函数.
正弦函数的图像
观察余弦函数的图像
这说明若将余弦曲线延着 y轴折叠,y轴两旁的部分能够互相重合 ,即余弦曲线关于y轴对称。
余弦函数是偶函数。
三、复习函数的单调性
函数的单调性反映了函数在一个区间上的走向。
请认真观察正余弦函数的图像,看看其是否具有这类性质?
先看正弦函数图像
由正弦函数的周期性知:
我们在来观察余弦函数的图像,看看是否有类似的特征。
再来观察余弦函数图像
由余弦函数的周期性知:
当x∈R时,即在整个定义域内并不单调,图像时而上升,时而下降,存在规范的单调区间.由于它们是周期函数,因此在考虑函数增减的问题时,只要研究一个周期即可。
四、函数的最大值与最小值
不求值,判断下列各式的符号.
分析:比较同名函数值的大小,往往可以利用函数的单调性,但需要考虑它是否在同一单调区间上,若是,即可判断,若不是,需化成同一单调区间后再作判断。
例2:
解:(1)
例3 求函数
解:令
由
例4 求下列函数的单调区间:
(1) y=2sin(-x )
解:
y=2sin(-x ) = -2sinx
所以:
解:
(4)
解:
定义域
解:
则 y= -|sinu| 大致图象如下:
例5:求下列函数的单调增区间:
解:
1、正余弦函数的周期性.
奇函数
偶函数
单调递增
单调递减
函数
求函数的单调区间:
1. 直接利用相关性质;
2. 复合函数的单调性;
3. 利用图象寻找单调区间。
2、正余弦函数的奇偶性、单调性
奇偶性
单调性(单调区间)
3、最大值与最小值
1 (2019四川)已知函数f(x)=sin(x- )(x∈R),下面结论错误的是( )
A.函数f(x)的最小正周期为2π
B.函数f(x)在区间 上是增函数
C.函数f(x)的图像关于直线x=0对称
D.函数f(x)是奇函数
D
解析:
2(2017全国)函数 f (x)= 的一个单调递增区间是( )
C
解析:
3 (2018广东)已知函数 ,
x∈R,则 是( )
D
A.最小正周期为 π 的奇函数
B.最小正周期为 的奇函数
C.最小正周期为 π 的偶函数
D.最小正周期为 的偶函数
解析:
1、 求下列三角函数的周期
即:f (2?+z)=f (z)
(2)令z=2x
∴ T=π
即:f(x+π)=f(x)
(3)令
∴ T=4π
2、已知
的大小关系是( )
B
A.
B.
D.
C.
D
4、函数 是( )
A.增函数
B.减函数
C.偶函数
D.奇函数
C
正弦函数的图像
余弦函数的图像
一、观察函数周期性
周期函数定义:对于函数f (x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有
f (x+T)=f (x)
那么,函数f (x)就叫做周期函数,非零常数T叫做这个函数的周期。
1、T是非零常数;
2、“每一个值”只要有一个反例,则f (x)就不为周期函数(如f (x0+t)?f (x0));
3、周期函数的周期T往往是多值的(如y=sinx,2?,4?,…,-2?,-4?,…都是它的周期);
4、周期T中最小的正数叫做f (x)的最小正周期(有些周期函数没有最小正周期).
正弦曲线:
周期性:
周期性:
余弦曲线:
例1.求下列函数的周期.
(2) ∵
解:
注:由上面的得出:
正弦函数的图像
二、观察正余弦函数图像奇偶性
余弦函数的图像
问题:它们的图像有什么特征?
观察可以看到正弦函数曲线关于原点O对称.正弦函数是奇函数.
正弦函数的图像
观察余弦函数的图像
这说明若将余弦曲线延着 y轴折叠,y轴两旁的部分能够互相重合 ,即余弦曲线关于y轴对称。
余弦函数是偶函数。
三、复习函数的单调性
函数的单调性反映了函数在一个区间上的走向。
请认真观察正余弦函数的图像,看看其是否具有这类性质?
先看正弦函数图像
由正弦函数的周期性知:
我们在来观察余弦函数的图像,看看是否有类似的特征。
再来观察余弦函数图像
由余弦函数的周期性知:
当x∈R时,即在整个定义域内并不单调,图像时而上升,时而下降,存在规范的单调区间.由于它们是周期函数,因此在考虑函数增减的问题时,只要研究一个周期即可。
四、函数的最大值与最小值
不求值,判断下列各式的符号.
分析:比较同名函数值的大小,往往可以利用函数的单调性,但需要考虑它是否在同一单调区间上,若是,即可判断,若不是,需化成同一单调区间后再作判断。
例2:
解:(1)
例3 求函数
解:令
由
例4 求下列函数的单调区间:
(1) y=2sin(-x )
解:
y=2sin(-x ) = -2sinx
所以:
解:
(4)
解:
定义域
解:
则 y= -|sinu| 大致图象如下:
例5:求下列函数的单调增区间:
解:
1、正余弦函数的周期性.
奇函数
偶函数
单调递增
单调递减
函数
求函数的单调区间:
1. 直接利用相关性质;
2. 复合函数的单调性;
3. 利用图象寻找单调区间。
2、正余弦函数的奇偶性、单调性
奇偶性
单调性(单调区间)
3、最大值与最小值
1 (2019四川)已知函数f(x)=sin(x- )(x∈R),下面结论错误的是( )
A.函数f(x)的最小正周期为2π
B.函数f(x)在区间 上是增函数
C.函数f(x)的图像关于直线x=0对称
D.函数f(x)是奇函数
D
解析:
2(2017全国)函数 f (x)= 的一个单调递增区间是( )
C
解析:
3 (2018广东)已知函数 ,
x∈R,则 是( )
D
A.最小正周期为 π 的奇函数
B.最小正周期为 的奇函数
C.最小正周期为 π 的偶函数
D.最小正周期为 的偶函数
解析:
1、 求下列三角函数的周期
即:f (2?+z)=f (z)
(2)令z=2x
∴ T=π
即:f(x+π)=f(x)
(3)令
∴ T=4π
2、已知
的大小关系是( )
B
A.
B.
D.
C.
D
4、函数 是( )
A.增函数
B.减函数
C.偶函数
D.奇函数
C
