1.4.3正切函数的性质与图形(共37张PPT)
文档属性
| 名称 | 1.4.3正切函数的性质与图形(共37张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 11:03:08 | ||
图片预览





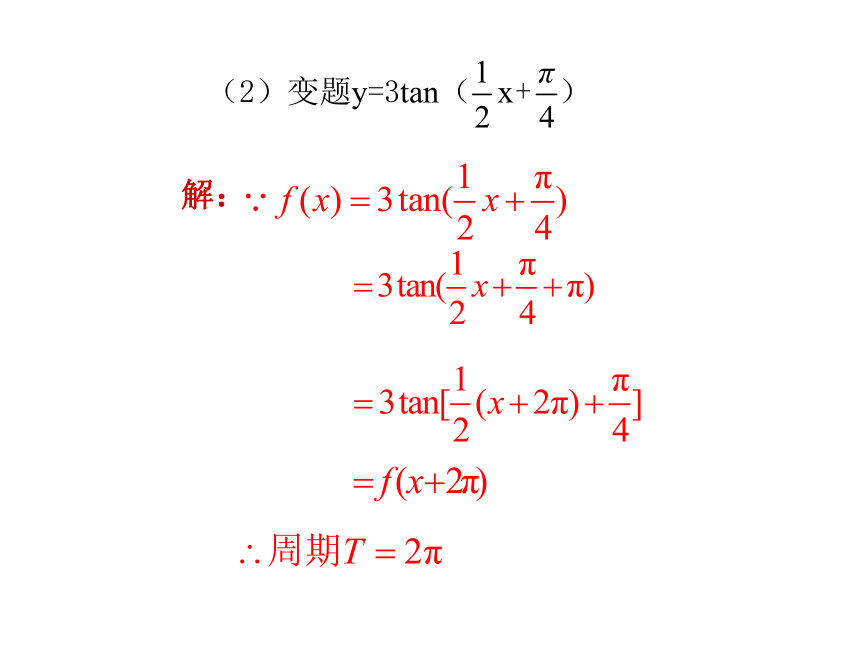



文档简介
(共37张PPT)
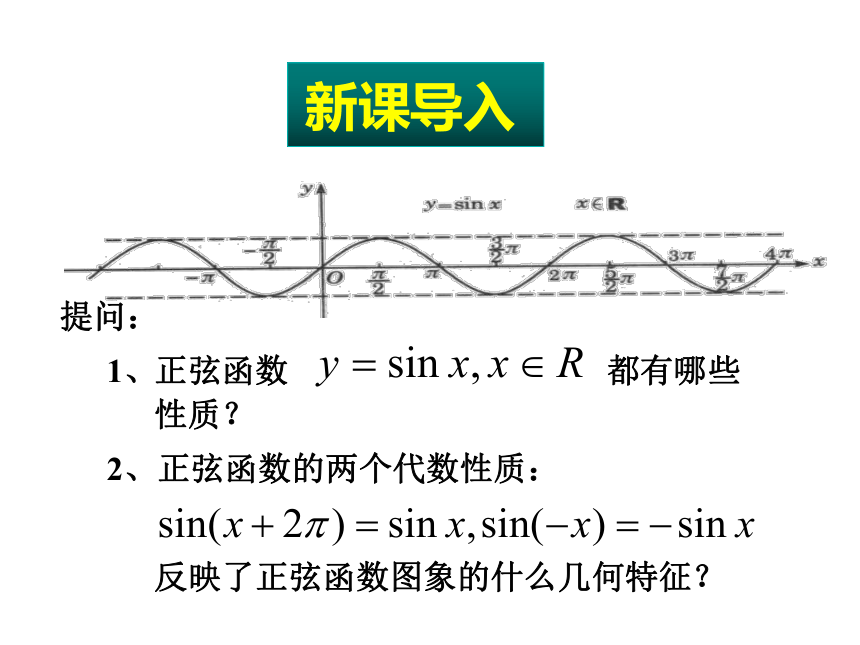
提问:
3、函数图象的每一个几何特征也都是函数性质的直观反映,函数的每一个代数性质反映在图象上都有其相应的几何特征;所以可借助于函数的图象来研究函数的性质;也可借助于函数的性质研究函数的图象,本节课就是从一个全新的角度来研究正切函数的性质与图象。
类比研究正弦和余弦函数的方法,从前面的学过的有关正切函数的知识中你认为有那些性质?
提问:
一、正切函数的定义域:
二、正切函数的周期性:
由 ,可知正切函数
是周期函数.
例1:求下列函数的周期:
由上面两例题,你能得到函数y=Atan(ωx+φ)的周期吗?
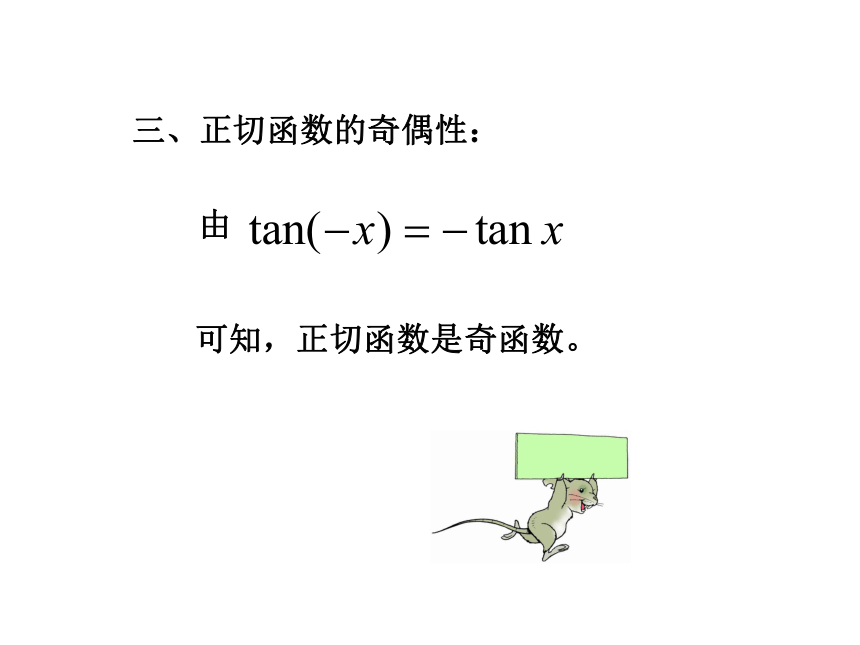
三、正切函数的奇偶性:
四、正切函数的单调性
2、借助多媒体,观察动态演示单位圆中的正切线的变化规律可以得出:
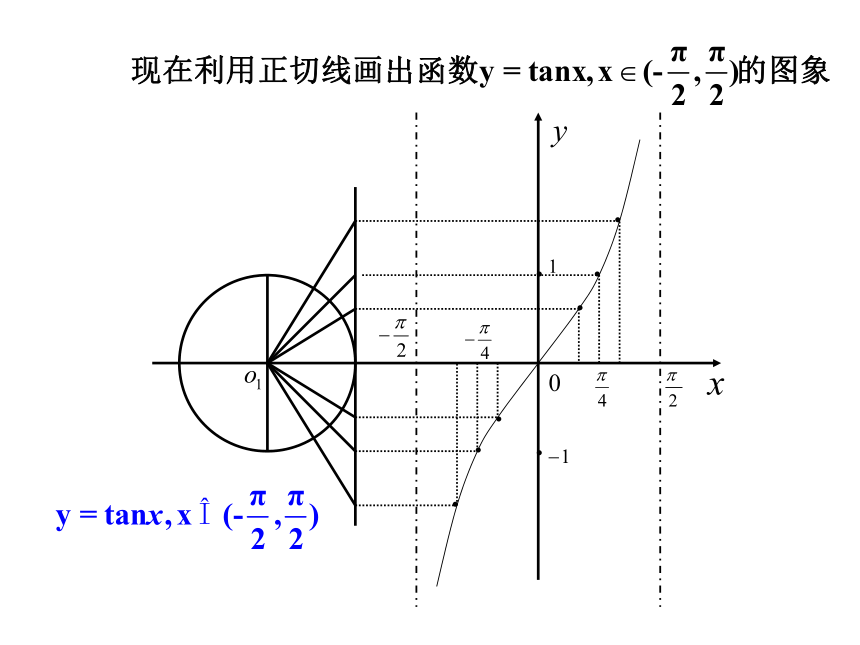
用正切线作正切函数图象:
画图:
作法:
(1) 等分:
(2) 作正切线
(3) 平移
(4) 连线
把单位圆右半圆分成8等份
利用正切函数的周期性,把图象向左,右扩展,得到正切函数
叫做正切曲线。
从图中可以看出,正切曲线是由被相互平行的直线
正切函数在 内是增函数,又由正切函数的周期性可知:正切函数在开区间 内都是增函数。
注意:正切函数只有增区间没有减区间。
例2:求下列的单调区间:
通过观察单位圆中的正切线的变化规律,我们可以得到:正切函数的值域是实数集R。
五、正切函数的值域
例3:不通过求值,比较下列各组中两个正切函数值的大小:
正切函数的主要性质总结如下:
定义域
值 域
周期性
奇偶性
单调性
例 题
例 题
例 题
例 题
例 题
例3:不通过求值,比较下列两个正切函数值的大小。
说明:比较两个正切型函数的大小,关键是把相应的角诱导到y=tanx的同一单调区间内,利用y=tanx的单调递增性来解决。
分析:利用周期函数定义及正切函数最小正周期为π。
例5:判断下列函数的奇偶性:
说明:函数具有奇、偶性的必要条件之一是定义域
关于原点对称,故验证f(-x)=f(-x)或
f(-x)= -f(x)成立前,要先判断定义域
是否关于原点对称。
例6:求下列函数的单调区间:
奇函数
R
单调增区间
奇偶性
周期
值域
定义域
1、直线 ( 为常数)与正切曲线 ( 为常数
且 )相交的相邻两点间的距离是( )
C
D
4、已知θ是三角形的一个内角,且tanθ≥-1,则θ的取值范围是( )
A.
C
C
C.
B .
D.以上都不对
5、求函数y=tan3x的定义域,值域,单调增区间。
解:
解:
解法1
7、
解:
解法2
7、
答案:
提问:
3、函数图象的每一个几何特征也都是函数性质的直观反映,函数的每一个代数性质反映在图象上都有其相应的几何特征;所以可借助于函数的图象来研究函数的性质;也可借助于函数的性质研究函数的图象,本节课就是从一个全新的角度来研究正切函数的性质与图象。
类比研究正弦和余弦函数的方法,从前面的学过的有关正切函数的知识中你认为有那些性质?
提问:
一、正切函数的定义域:
二、正切函数的周期性:
由 ,可知正切函数
是周期函数.
例1:求下列函数的周期:
由上面两例题,你能得到函数y=Atan(ωx+φ)的周期吗?
三、正切函数的奇偶性:
四、正切函数的单调性
2、借助多媒体,观察动态演示单位圆中的正切线的变化规律可以得出:
用正切线作正切函数图象:
画图:
作法:
(1) 等分:
(2) 作正切线
(3) 平移
(4) 连线
把单位圆右半圆分成8等份
利用正切函数的周期性,把图象向左,右扩展,得到正切函数
叫做正切曲线。
从图中可以看出,正切曲线是由被相互平行的直线
正切函数在 内是增函数,又由正切函数的周期性可知:正切函数在开区间 内都是增函数。
注意:正切函数只有增区间没有减区间。
例2:求下列的单调区间:
通过观察单位圆中的正切线的变化规律,我们可以得到:正切函数的值域是实数集R。
五、正切函数的值域
例3:不通过求值,比较下列各组中两个正切函数值的大小:
正切函数的主要性质总结如下:
定义域
值 域
周期性
奇偶性
单调性
例 题
例 题
例 题
例 题
例 题
例3:不通过求值,比较下列两个正切函数值的大小。
说明:比较两个正切型函数的大小,关键是把相应的角诱导到y=tanx的同一单调区间内,利用y=tanx的单调递增性来解决。
分析:利用周期函数定义及正切函数最小正周期为π。
例5:判断下列函数的奇偶性:
说明:函数具有奇、偶性的必要条件之一是定义域
关于原点对称,故验证f(-x)=f(-x)或
f(-x)= -f(x)成立前,要先判断定义域
是否关于原点对称。
例6:求下列函数的单调区间:
奇函数
R
单调增区间
奇偶性
周期
值域
定义域
1、直线 ( 为常数)与正切曲线 ( 为常数
且 )相交的相邻两点间的距离是( )
C
D
4、已知θ是三角形的一个内角,且tanθ≥-1,则θ的取值范围是( )
A.
C
C
C.
B .
D.以上都不对
5、求函数y=tan3x的定义域,值域,单调增区间。
解:
解:
解法1
7、
解:
解法2
7、
答案:
