1.5函数y=Asin(wx+φ)的图象(共40张PPT)
文档属性
| 名称 | 1.5函数y=Asin(wx+φ)的图象(共40张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 11:04:03 | ||
图片预览








文档简介
(共40张PPT)
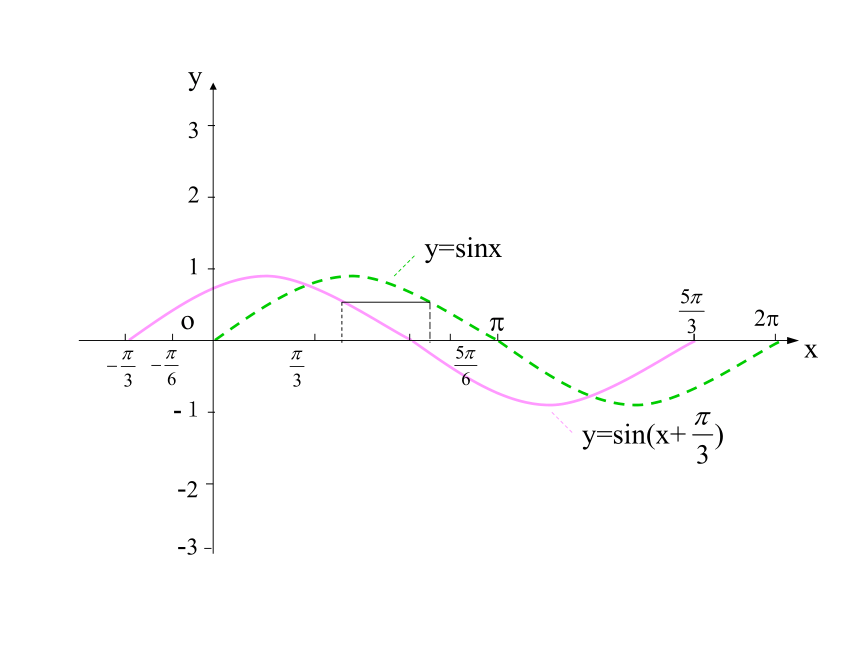
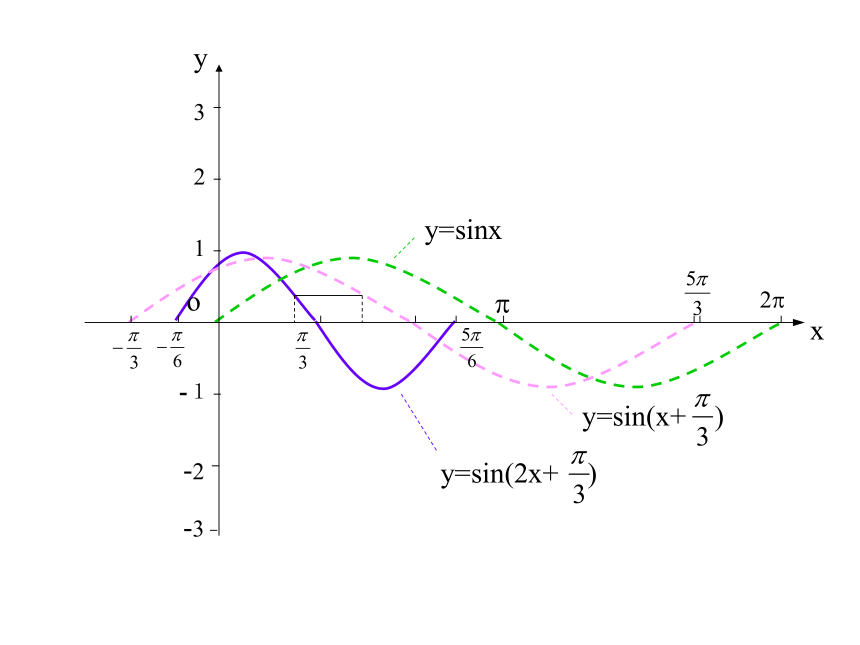
如图,当两曲线纵坐标相同时,观察它们的横坐标的关系。
如图,当两条曲线纵坐标相同时,观察它们的横坐标的关系。
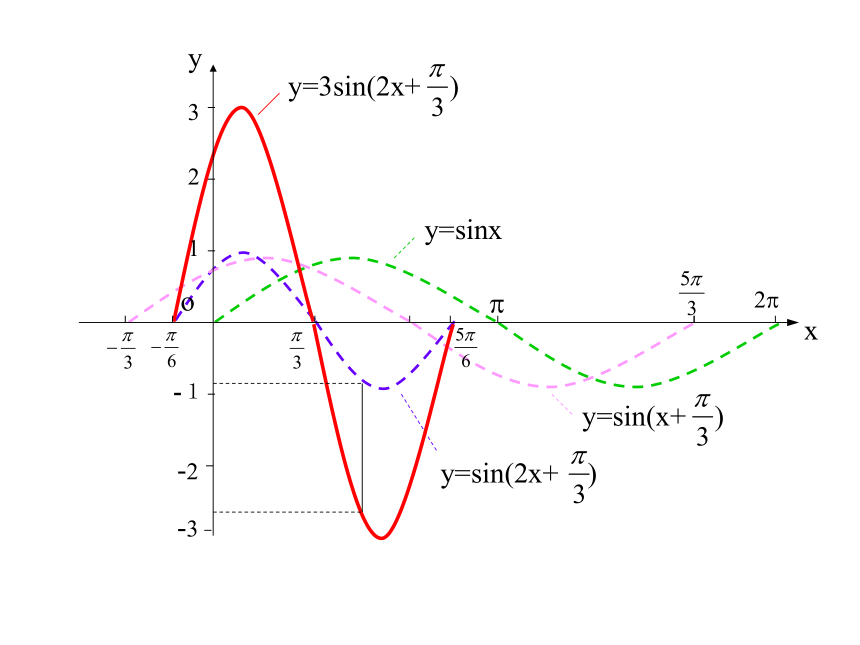
如图,两条曲线横坐标相同时,观察它们的纵坐标的关系。
通过实验可以看到,当A取其它的值也有类似的情况.因此,y=Asin(ωx+φ) 的图象,可以看作是把y=sin( ωx+φ )上的所有点的纵坐标伸长(当A>1时)或 缩短(当0列表并描点作图:
0
1
0
0
0
0
0
0
0
0
-1
-2
2
列表:
0
0
0
0
0
0
0
0
1
-1
1
-1
解:列表
X=x+
sin(x+
)
0
2
-
0
1
0
-1
0
x
因为T=?,所以用“五点法”先作长度为一个周期的闭区间上的简图.
(3)连线:
(4)根据周期性将作出的简图左右扩展。
2?
?
设:
则:
1、 振幅变换
2、 平移变换
1、 平移变换
2、 振幅变换
当函数y=Asin(ωx+φ),(A>0,ω>0),x ∈[0,+∞)表示一个振动量时,A就表示这个量振动时离开平衡位置的最大距离,通常把它叫做这个振动的振幅;
往复振动一次所需要的时间T=2π/ω,它叫做振动的周期;
单位时间内往复振动的次数f=1/T=ω/2π,它叫做振动的频率;
ωx+φ叫做相位,φ叫做初相(即当x=0时的相位)。
例6:如图所示,是一个质点的振动图像,根据图像回答下列各问:
(1)振动的振幅__________。
(2)振动的频率__________。
(3)振动的周期__________。
5cm
5/4
0.8 s
1(2017广东)已知简谐运动 的图像经过点(0,1),则该简谐运动的最小正周期T和 初相分别为( )
A
解析:
步骤1
步骤2
步骤3
步骤4
步骤5
沿x轴 平行移动
横坐标 伸长或缩短
纵坐标 伸长或缩短
沿x轴 扩展
1.将函数y=sinx的图像上每一点的_____坐标不变,___坐标_____________,可得到函数的图像。
纵
横
C
4、函数 的图象可以由函数 的图象经过下列哪种变换得到( )
A
D
6、如图是函数 的图象,那么 ( )
C
A
2?
?
如图,当两曲线纵坐标相同时,观察它们的横坐标的关系。
如图,当两条曲线纵坐标相同时,观察它们的横坐标的关系。
如图,两条曲线横坐标相同时,观察它们的纵坐标的关系。
通过实验可以看到,当A取其它的值也有类似的情况.因此,y=Asin(ωx+φ) 的图象,可以看作是把y=sin( ωx+φ )上的所有点的纵坐标伸长(当A>1时)或 缩短(当0
0
1
0
0
0
0
0
0
0
0
-1
-2
2
列表:
0
0
0
0
0
0
0
0
1
-1
1
-1
解:列表
X=x+
sin(x+
)
0
2
-
0
1
0
-1
0
x
因为T=?,所以用“五点法”先作长度为一个周期的闭区间上的简图.
(3)连线:
(4)根据周期性将作出的简图左右扩展。
2?
?
设:
则:
1、 振幅变换
2、 平移变换
1、 平移变换
2、 振幅变换
当函数y=Asin(ωx+φ),(A>0,ω>0),x ∈[0,+∞)表示一个振动量时,A就表示这个量振动时离开平衡位置的最大距离,通常把它叫做这个振动的振幅;
往复振动一次所需要的时间T=2π/ω,它叫做振动的周期;
单位时间内往复振动的次数f=1/T=ω/2π,它叫做振动的频率;
ωx+φ叫做相位,φ叫做初相(即当x=0时的相位)。
例6:如图所示,是一个质点的振动图像,根据图像回答下列各问:
(1)振动的振幅__________。
(2)振动的频率__________。
(3)振动的周期__________。
5cm
5/4
0.8 s
1(2017广东)已知简谐运动 的图像经过点(0,1),则该简谐运动的最小正周期T和 初相分别为( )
A
解析:
步骤1
步骤2
步骤3
步骤4
步骤5
沿x轴 平行移动
横坐标 伸长或缩短
纵坐标 伸长或缩短
沿x轴 扩展
1.将函数y=sinx的图像上每一点的_____坐标不变,___坐标_____________,可得到函数的图像。
纵
横
C
4、函数 的图象可以由函数 的图象经过下列哪种变换得到( )
A
D
6、如图是函数 的图象,那么 ( )
C
A
2?
?
