必修4第一章 三角函数章末复习(共24张PPT)
文档属性
| 名称 | 必修4第一章 三角函数章末复习(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 576.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
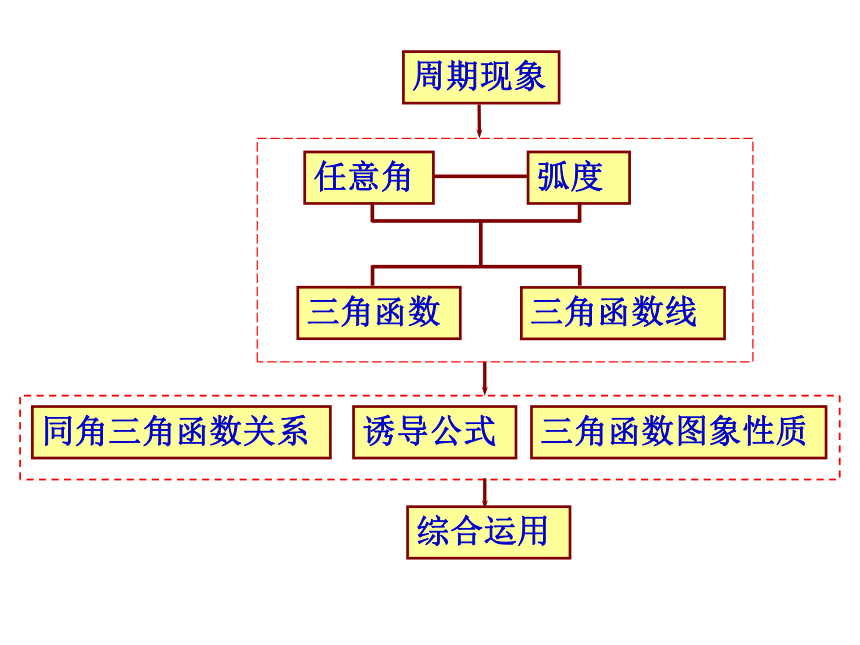
第一章 三角函数
1.1任意角和弧度制
1.2任意角的三角函数
1.3三角函数的诱导公式
1.4三角函数的图象与性质
1.5函数y=Asin(wx+φ)的图象
1.6三角函数模型的简单应用
1、利用单位圆研究任意角的三角函数,并用集合与对应的语言来刻画,利用几何直观有利于抽象概念的理解。
2、利用单位圆上点的坐标定义三角函数,从单位圆关于坐标轴,直线y=x原点等的对称性出发研究诱导公式。
3、利用数形结合的思想熟练把握三角函数的形状特征,利用图像研究性质,反过来再根据性质进一步认识函数的图像,充分体现了数形结合的思想方法。
1.1.1 任意角
1、任意角的概念
正角:射线按逆时针方向旋转形成的角;
负角:射线按顺时针方向旋转形成的角;
零角:射线不作旋转形成的角。
3、终边与角α相同的角
α+K×360°,K∈Z
(1)置角的顶点于原点;
(2)始边重合于X轴的正半轴。
2、象限角
终边落在第几象限就是第几象限角
1.1.2 弧度制
把长度等于半径长的弧所对的圆心角叫做1弧度的角。
定义:
定义域为R;
定义域为R;
定义域为
三角函数(正弦,余弦,正切)都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数.
(由于角的集合与实数集合之间可以建立一一对应关系,三角函数可以看成是自变量为实数的函数.)
所以三角函数可以记为:
1、任意角的三角函数定义
1.2.1任意角的三角函数
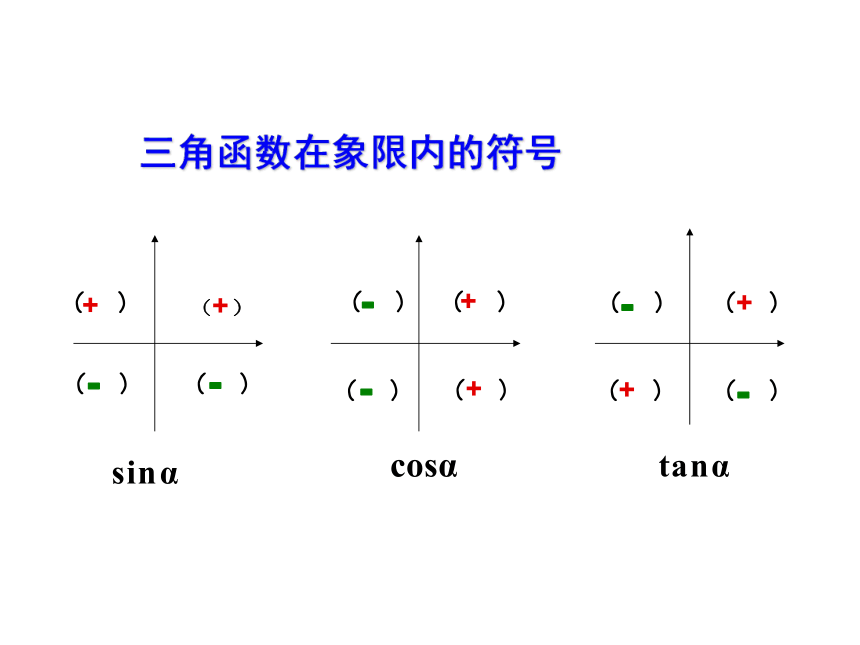
三角函数在象限内的符号
( )
+
+
-
-
+
+
-
-
+
+
-
-
应用
(1)判断符号
(2)求值
3、公式一(诱导公式)
(3)利用平方关系时,往往要开方,因此要先根据角所在象限确定符号,即要就角所在象限进行分类讨论。
1.2.2同角三角函数的基本关系
我们可以用下面一段话来概括公式一~四: , , 的三角函数值,等于α的同名函数值, 前面加上一个把α看成锐角时原函数值的符号。
公式一、二、三、四、都叫做诱导公式。
简化成“函数名不变,符号看象限”的口诀。
1.3三角函数的诱导公式
公式五、公式六概括如下:
简化成“奇变偶不变,符号看象限”的口诀。
2、决定正弦函数、余弦函数图像的五个关键点是用五点法作简图的依据;
3、作三角函数的图像可以用五点法作简图,也可以通过函数图形的基本变换来实现。
1、用单位圆中的正弦线作正弦函数的图象,及通过平移得到余弦函数的图像;
1.4.1正弦函数、余弦函数的图象
1、正余弦函数的周期性。
1.4.2正、余弦函数的性质
奇函数
偶函数
单调递增
单调递减
函数
求函数的单调区间:
(1)直接利用相关性质;
(2)复合函数的单调性;
(3)利用图象寻找单调区间。
2、正余弦函数的奇偶性、单调性
奇偶性
单调性(单调区间)
3、最大值与最小值
奇函数
R
单调增区间
奇偶性
周期
值域
定义域
1.4.3正切函数的性质及图象
1.5函数y=Asin(wx+φ)的图象
步骤1
步骤2
步骤3
步骤4
步骤5
沿x轴 平行移动
横坐标 伸长或缩短
纵坐标 伸长或缩短
沿x轴 扩展
1.6三角函数模型的简单应用
1、根据角的终边所在的象限,掌握象限角的概念 。
3、用诱导公式将任意角的三角函数化成某个锐角的三角函数。
2、根据一个角的某一个三角函数值,求出该角的其他三角函数值(当然用三角函数的定义求解会更方便);化简同角的三角函数式;证明同角的三角恒等式。
1、对函数性质理解不透。
3、抓不住图象平移实质。
4、求函数解析式时忽视作图法而致错。
2、在计算或化简三角函数关系式时,常需要对角的范围以及相应三角函数值的正负情况进行讨论。
第一章 三角函数
1.1任意角和弧度制
1.2任意角的三角函数
1.3三角函数的诱导公式
1.4三角函数的图象与性质
1.5函数y=Asin(wx+φ)的图象
1.6三角函数模型的简单应用
1、利用单位圆研究任意角的三角函数,并用集合与对应的语言来刻画,利用几何直观有利于抽象概念的理解。
2、利用单位圆上点的坐标定义三角函数,从单位圆关于坐标轴,直线y=x原点等的对称性出发研究诱导公式。
3、利用数形结合的思想熟练把握三角函数的形状特征,利用图像研究性质,反过来再根据性质进一步认识函数的图像,充分体现了数形结合的思想方法。
1.1.1 任意角
1、任意角的概念
正角:射线按逆时针方向旋转形成的角;
负角:射线按顺时针方向旋转形成的角;
零角:射线不作旋转形成的角。
3、终边与角α相同的角
α+K×360°,K∈Z
(1)置角的顶点于原点;
(2)始边重合于X轴的正半轴。
2、象限角
终边落在第几象限就是第几象限角
1.1.2 弧度制
把长度等于半径长的弧所对的圆心角叫做1弧度的角。
定义:
定义域为R;
定义域为R;
定义域为
三角函数(正弦,余弦,正切)都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数.
(由于角的集合与实数集合之间可以建立一一对应关系,三角函数可以看成是自变量为实数的函数.)
所以三角函数可以记为:
1、任意角的三角函数定义
1.2.1任意角的三角函数
三角函数在象限内的符号
( )
+
+
-
-
+
+
-
-
+
+
-
-
应用
(1)判断符号
(2)求值
3、公式一(诱导公式)
(3)利用平方关系时,往往要开方,因此要先根据角所在象限确定符号,即要就角所在象限进行分类讨论。
1.2.2同角三角函数的基本关系
我们可以用下面一段话来概括公式一~四: , , 的三角函数值,等于α的同名函数值, 前面加上一个把α看成锐角时原函数值的符号。
公式一、二、三、四、都叫做诱导公式。
简化成“函数名不变,符号看象限”的口诀。
1.3三角函数的诱导公式
公式五、公式六概括如下:
简化成“奇变偶不变,符号看象限”的口诀。
2、决定正弦函数、余弦函数图像的五个关键点是用五点法作简图的依据;
3、作三角函数的图像可以用五点法作简图,也可以通过函数图形的基本变换来实现。
1、用单位圆中的正弦线作正弦函数的图象,及通过平移得到余弦函数的图像;
1.4.1正弦函数、余弦函数的图象
1、正余弦函数的周期性。
1.4.2正、余弦函数的性质
奇函数
偶函数
单调递增
单调递减
函数
求函数的单调区间:
(1)直接利用相关性质;
(2)复合函数的单调性;
(3)利用图象寻找单调区间。
2、正余弦函数的奇偶性、单调性
奇偶性
单调性(单调区间)
3、最大值与最小值
奇函数
R
单调增区间
奇偶性
周期
值域
定义域
1.4.3正切函数的性质及图象
1.5函数y=Asin(wx+φ)的图象
步骤1
步骤2
步骤3
步骤4
步骤5
沿x轴 平行移动
横坐标 伸长或缩短
纵坐标 伸长或缩短
沿x轴 扩展
1.6三角函数模型的简单应用
1、根据角的终边所在的象限,掌握象限角的概念 。
3、用诱导公式将任意角的三角函数化成某个锐角的三角函数。
2、根据一个角的某一个三角函数值,求出该角的其他三角函数值(当然用三角函数的定义求解会更方便);化简同角的三角函数式;证明同角的三角恒等式。
1、对函数性质理解不透。
3、抓不住图象平移实质。
4、求函数解析式时忽视作图法而致错。
2、在计算或化简三角函数关系式时,常需要对角的范围以及相应三角函数值的正负情况进行讨论。
