2020年冀教新版七年级数学下册《第7章 相交线与平行线》单元测试卷(解析版)
文档属性
| 名称 | 2020年冀教新版七年级数学下册《第7章 相交线与平行线》单元测试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 427.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-07 00:00:00 | ||
图片预览



文档简介
2020年冀教新版七年级数学下册《第7章 相交线与平行线》单元测试卷
一.选择题(共12小题)
1.平面内三条直线的交点个数可能有( )
A.1个或3个 B.2个或3个
C.1个或2个或3个 D.0个或1个或2个或3个
2.如图,三条直线a、b、c相交于一点,则∠1+∠2+∠3=( )
A.360° B.180° C.120° D.90
3.如图,点O为直线AB上一点,OC⊥OD.如果∠1=35°,那么∠2的度数是( )
A.35° B.45° C.55° D.65°
4.下列语句是命题的是( )
(1)两点之间,线段最短;
(2)如果两个角的和是90度,那么这两个角互余.
(3)请画出两条互相平行的直线;
(4)过直线外一点作已知直线的垂线.
A.(1)(2) B.(3)(4) C.(2)(3) D.(1)(4)
5.下列命题中是假命题的是( )
A.同旁内角互补,两直线平行
B.垂线段最短
C.在同一平面内,过一点有且只有一条直线与已知直线垂直
D.直线外一点到这条直线的垂线段叫做点到直线的距离
6.下列命题中,真命题是( )
A.相等的角是对顶角
B.两条直线被第三条直线所截,同位角相等
C.在同一平面内,垂直于同一条直线的两条直线平行
D.同旁内角互补
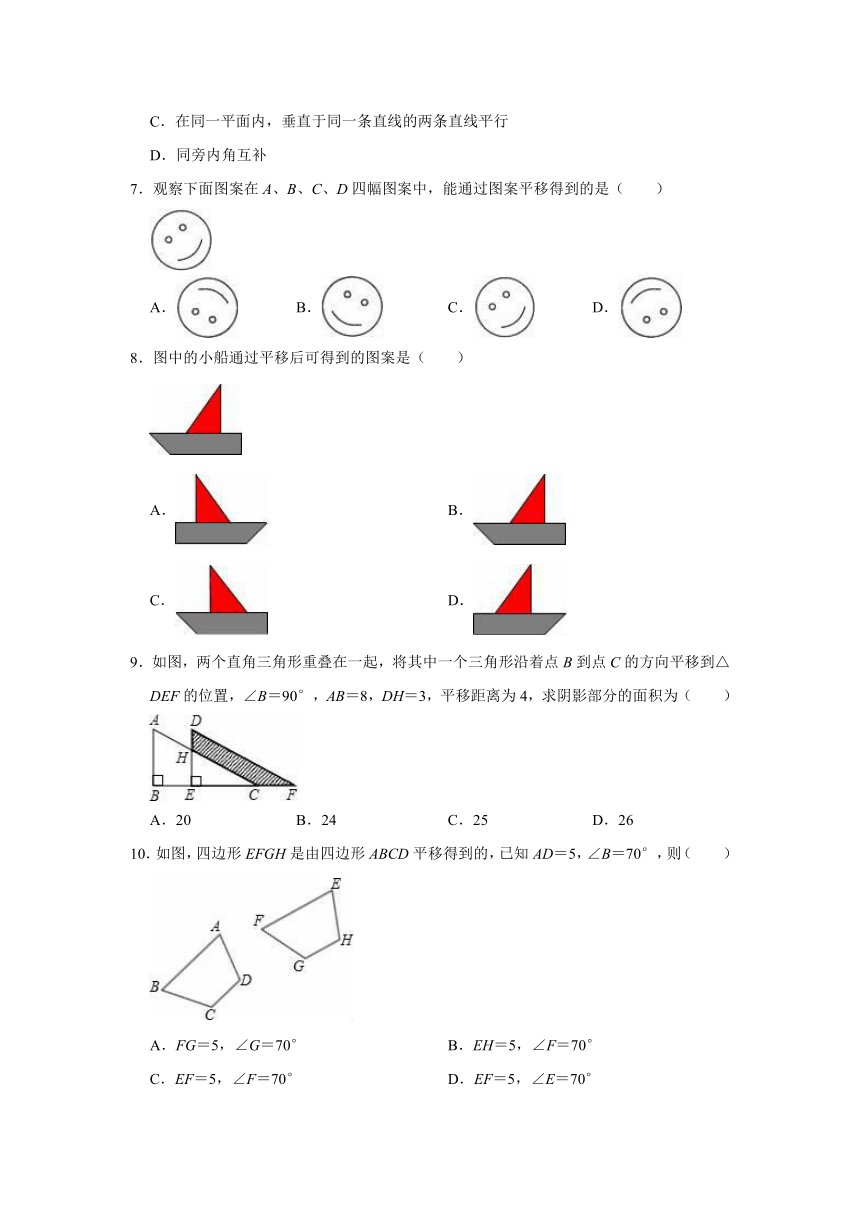
7.观察下面图案在A、B、C、D四幅图案中,能通过图案平移得到的是( )
A. B. C. D.
8.图中的小船通过平移后可得到的图案是( )
A. B.
C. D.
9.如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,∠B=90°,AB=8,DH=3,平移距离为4,求阴影部分的面积为( )
A.20 B.24 C.25 D.26
10.如图,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=70°,则( )
A.FG=5,∠G=70° B.EH=5,∠F=70°
C.EF=5,∠F=70° D.EF=5,∠E=70°
11.如图所示的图案分别是大众、奥迪、奔驰、三菱汽车的车标,其中,可以看作由“基本图案”经过平移得到的是( )
A. B.
C. D.
12.下列如图所示的图案,分别是奔驰、奥迪、三菱、大众汽车的车标,其中可以看作由“基本图案”经过平移得到的是( )
A. B.
C. D.
二.填空题(共8小题)
13.三条直线两两相交,最少有 个交点,最多有 个交点.
14.若∠1的对顶角是∠2,∠2的邻补角是∠3,∠3=45°,则∠1的度数为 .
15.“同位角相等”的逆命题是 .
16.命题“全等三角形的对应角相等”的逆命题是 ,这个逆命题是 (填“真”或“假”).
17.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的矩形荷塘上架设小桥.若荷塘周长为280m,且桥宽忽略不计,则小桥总长为 m.
18.在高3米,水平距离为4米的楼梯表面铺地毯,地毯的长度至少需要 米.
19.如图,根据长方形中的数据,计算阴影部分的面积为 .
20.如图所示,由三角形ABC平移得到的三角形有 个.
三.解答题(共8小题)
21.如图,直线AB、CD、EF相交于点O.
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.
22.如图①②所示,将两个相同三角板的两个直角顶点O重合在一起,像图①②那样放置.
(1)若∠BOC=60°,如图①,猜想∠AOD的度数;
(2)若∠BOC=70°,如图②,猜想∠AOD的度数;
(3)猜想∠AOD和∠BOC的关系,并写出理由.
23.判断下列命题的真假,若是假命题,举出反例.
(1)若两个角不是对顶角,则这两个角不相等;
(2)若ab=0,则a+b=0.
24.如图,有三个论断①∠1=∠2;②∠B=∠D;③∠A=∠C,请从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性.
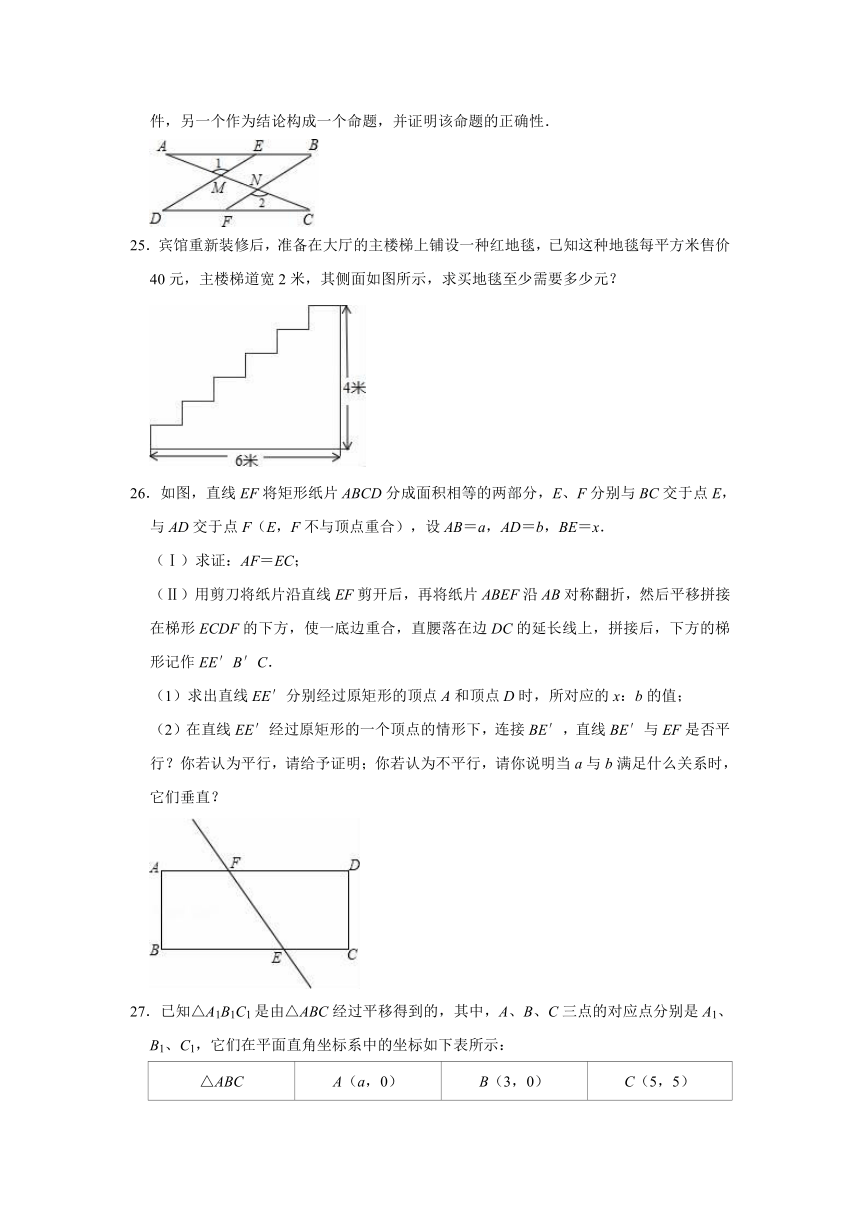
25.宾馆重新装修后,准备在大厅的主楼梯上铺设一种红地毯,已知这种地毯每平方米售价40元,主楼梯道宽2米,其侧面如图所示,求买地毯至少需要多少元?
26.如图,直线EF将矩形纸片ABCD分成面积相等的两部分,E、F分别与BC交于点E,与AD交于点F(E,F不与顶点重合),设AB=a,AD=b,BE=x.
(Ⅰ)求证:AF=EC;
(Ⅱ)用剪刀将纸片沿直线EF剪开后,再将纸片ABEF沿AB对称翻折,然后平移拼接在梯形ECDF的下方,使一底边重合,直腰落在边DC的延长线上,拼接后,下方的梯形记作EE′B′C.
(1)求出直线EE′分别经过原矩形的顶点A和顶点D时,所对应的x:b的值;
(2)在直线EE′经过原矩形的一个顶点的情形下,连接BE′,直线BE′与EF是否平行?你若认为平行,请给予证明;你若认为不平行,请你说明当a与b满足什么关系时,它们垂直?
27.已知△A1B1C1是由△ABC经过平移得到的,其中,A、B、C三点的对应点分别是A1、B1、C1,它们在平面直角坐标系中的坐标如下表所示:
△ABC A(a,0) B(3,0) C(5,5)
△A1B1C1 A1(﹣3,2) B1(﹣1,b) C1(c,7)
(1)观察表中各对应点坐标的变化,并填空:a= ,b= ,c= ;
(2)在如图的平面直角坐标系中画出△ABC及△A1B1C1;
(3)△A1B1C1的面积是 .
28.把小船ABCD通过平移后到A′B′C′D′的位置,请你根据题中信息,画出平移后的小船位置.
2020年冀教新版七年级数学下册《第7章 相交线与平行线》单元测试卷
参考答案与试题解析
一.选择题(共12小题)
1.平面内三条直线的交点个数可能有( )
A.1个或3个 B.2个或3个
C.1个或2个或3个 D.0个或1个或2个或3个
【分析】根据相交线的定义,作出所有可能的图形即可得解.
【解答】解:如图所示,
分别有0个交点,1个交点,2个交点,3个交点,
∴交点个数可能有0个或1个或2个或3个.
故选:D.
【点评】本题考查了相交线的知识,穷举出所有的可能情况并作出图形是解题的关键.
2.如图,三条直线a、b、c相交于一点,则∠1+∠2+∠3=( )
A.360° B.180° C.120° D.90
【分析】利用对顶角相等,可知∠1+∠2+∠3的和是360°的一半.
【解答】解:因为对顶角相等,所以∠1+∠2+∠3=×360°=180°.
故选:B.
【点评】本题考查对顶角的性质,是一个需要熟记的内容.
3.如图,点O为直线AB上一点,OC⊥OD.如果∠1=35°,那么∠2的度数是( )
A.35° B.45° C.55° D.65°
【分析】根据垂线的定义,可得∠COD,根据角的和差,可得答案.
【解答】解:∵OC⊥OD,
∴∠COD=90°.
由角的和差,得
∠2=180°﹣∠COD﹣∠1
=180°﹣90°﹣35°=55°,
故选:C.
【点评】本题考查了垂线的定义,利用垂线的定义是解题关键.
4.下列语句是命题的是( )
(1)两点之间,线段最短;
(2)如果两个角的和是90度,那么这两个角互余.
(3)请画出两条互相平行的直线;
(4)过直线外一点作已知直线的垂线.
A.(1)(2) B.(3)(4) C.(2)(3) D.(1)(4)
【分析】判断一件事情的语句叫命题,命题都由题设和结论两部分组成,依此对四个小题进行逐一分析即可;
【解答】解:(1)两点之间,线段最短符合命题定义,正确;
(2)如果两个角的和是90度,那么这两个角互余,符合命题定义,正确.
(3)请画出两条互相平行的直线只是做了陈述,不是命题,错误;
(4)过直线外一点作已知直线的垂线没有做出判断,不是命题,错误,
故选:A.
【点评】本题考查了命题的概念:一般的,在数学中我们把用语言、符号或式子表达的,可以判断真假的陈述句叫做命题.其中判断为真的语句叫做真命题,判断为假的语句叫做假命题.注意命题是一个能够判断真假的陈述句.
5.下列命题中是假命题的是( )
A.同旁内角互补,两直线平行
B.垂线段最短
C.在同一平面内,过一点有且只有一条直线与已知直线垂直
D.直线外一点到这条直线的垂线段叫做点到直线的距离
【分析】根据平行线的判定对A进行判断;
根据垂线段公理对B进行判断;
根据过一点有且只有一条直线与原直线垂直对C进行判断;
根据点到直线的距离的定义对D进行判断.
【解答】解:A、同旁内角互补,两直线平行,所以A选项为真命题;
B、直线外一点与直线上所有点的连线段中,垂线段最短,所以B选项为真命题;
C、在同一平面内,过一点有且只有一条直线与已知直线垂直,所以C选项为真命题;
D、直线外一点到这条直线的垂线段的长叫做点到直线的距离,所以D选项为假命题.
故选:D.
【点评】本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.
6.下列命题中,真命题是( )
A.相等的角是对顶角
B.两条直线被第三条直线所截,同位角相等
C.在同一平面内,垂直于同一条直线的两条直线平行
D.同旁内角互补
【分析】分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.
【解答】解:A、错误,对顶角相等但相等的角不一定是对顶角;
B、错误,当被截的直线平行时形成的同位角才相等;
C、正确,必须强调在同一平面内;
D、错误,两直线平行同旁内角才互补.
故选:C.
【点评】主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
7.观察下面图案在A、B、C、D四幅图案中,能通过图案平移得到的是( )
A. B. C. D.
【分析】找到平移前后形状与大小没有改变,并且对应点的连线平行且相等的图形即可.
【解答】解:A、对应点的连线相交,不能通过平移得到,不符合题意;
B、对应点的连线相交,不能通过平移得到,不符合题意;
C、可通过平移得到,符合题意;
D、对应点的连线相交,不能通过平移得到,不符合题意;
故选:C.
【点评】本题需抓住平移前后对应点的连线平行且相等这个知识点进行解答.
8.图中的小船通过平移后可得到的图案是( )
A. B.
C. D.
【分析】根据平移的概念:在平面内,把一个图形整体沿某一的方向移动,这种图形的平行移动,叫做平移变换,简称平移可以选出答案.
【解答】解:根据平移定义可得:图中的小船通过平移后可得到的图案是B.
故选:B.
【点评】此题主要考查了生活中的平移,关键是掌握平移是指图形的平行移动,平移时图形中所有点移动的方向一致,并且移动的距离相等.
9.如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,∠B=90°,AB=8,DH=3,平移距离为4,求阴影部分的面积为( )
A.20 B.24 C.25 D.26
【分析】由S△ABC=S△DEF,推出S四边形ABEH=S阴即可解决问题;
【解答】解:∵平移距离为4,
∴BE=4,
∵AB=8,DH=3,
∴EH=8﹣3=5,
∵S△ABC=S△DEF,
∴S四边形ABEH=S阴
∴阴影部分的面积为=×(8+5)×4=26
故选:D.
【点评】此题主要考查了平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等,要熟练掌握.
10.如图,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=70°,则( )
A.FG=5,∠G=70° B.EH=5,∠F=70°
C.EF=5,∠F=70° D.EF=5,∠E=70°
【分析】经过平移,对应线段平行(或共线)且相等,对应角相等,对应点所连接的线段平行且相等.
【解答】解:在四边形EFGH,EH是AD的对应边,∠F是∠B的对应角,
∵AD=5,∠B=70°,故EH=5,∠F=70°.
故选:B.
【点评】解题的关键是利用平移的性质,找准对应边、对应角.
11.如图所示的图案分别是大众、奥迪、奔驰、三菱汽车的车标,其中,可以看作由“基本图案”经过平移得到的是( )
A. B.
C. D.
【分析】根据平移不改变图形的形状和大小,将题中所示的图案通过平移后可以得到的图案是B.
【解答】解:观察图形可知,图案B可以看作由“基本图案”经过平移得到.
故选:B.
【点评】本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转,而误选A、C、D.
12.下列如图所示的图案,分别是奔驰、奥迪、三菱、大众汽车的车标,其中可以看作由“基本图案”经过平移得到的是( )
A. B.
C. D.
【分析】根据平移的性质:不改变图形的形状和大小,不可旋转与翻转,将题中所示的图案通过平移后可以得到的图案是B.
【解答】解:观察图形可知,图案C可以看作由“基本图案”经过平移得到.
故选:B.
【点评】此题主要考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转,而导致错选.
二.填空题(共8小题)
13.三条直线两两相交,最少有 1 个交点,最多有 3 个交点.
【分析】最少的交点个数即其相交于一点,而最多也就能构成一个三角形,即三个交点.
【解答】解:如图所示:
两两相交的直线,其最少有1个交点,即三条直线相交于一点;
最多有三个交点,即其构成一个三角形,共三个交点.
故答案为1,3.
【点评】本题主要考查了相交线,关键是考虑全面,不要漏解.
14.若∠1的对顶角是∠2,∠2的邻补角是∠3,∠3=45°,则∠1的度数为 135° .
【分析】根据对顶角相等、邻补角互补的性质求解.
【解答】解:∵∠2的邻补角是∠3,∠3=45°,
∴∠2=180°﹣∠3=135°.
∵∠1的对顶角是∠2,
∴∠1=∠2=135°.
【点评】本题考查对顶角的性质以及邻补角的定义,是一个需要熟记的内容.
15.“同位角相等”的逆命题是 相等的角是同位角 .
【分析】“同位角相等”的题设为两个角为同位角,结论为这两个角相等,然后交换题设与结论即可得到原命题的逆命题.
【解答】解:“同位角相等”的逆命题为:相等的两个角为同位角.
故答案为:相等的角是同位角.
【点评】本题考查了逆命题,关键找出题设和结论部分,然后交换题设和结论即为逆命题.
16.命题“全等三角形的对应角相等”的逆命题是 对应角相等的三角形是全等三角形 ,这个逆命题是 假 (填“真”或“假”).
【分析】根据逆命题的概念,交换原命题的题设与结论即可的出原命题的逆命题,进而判断它的真假.
【解答】解:命题“全等三角形对应角相等”的题设是“全等三角形”,结论是“对应角相等”,
故其逆命题是对应角相等的三角形是全等三角形,它是一个假命题.
故答案为:对应角相等的三角形是全等三角形,假.
【点评】此题考查了互逆命题的知识,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题.
17.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的矩形荷塘上架设小桥.若荷塘周长为280m,且桥宽忽略不计,则小桥总长为 140 m.
【分析】利用平移的性质直接得出答案即可.
【解答】解:根据题意得出:小桥可以平移到矩形的边上,得出小桥的长等于矩形的长与宽的和,
故小桥总长为:280÷2=140(m).
故答案为:140.
【点评】此题主要考查了生活中的平移,根据已知正确平移小桥是解题关键.
18.在高3米,水平距离为4米的楼梯表面铺地毯,地毯的长度至少需要 7 米.
【分析】把楼梯的水平线段向下平移,竖直线段向右平移可得地毯长度为水平距离与高的和.
【解答】解:地毯长度至少需3+4=7米.
故答案为:7.
【点评】此题主要考查了生活中的平移及平移的性质,根据已知得出地毯的长度应等于水平距离与高的和是解题关键.
19.如图,根据长方形中的数据,计算阴影部分的面积为 104 .
【分析】两个阴影图形可以平移到一个长方形中去,故根据长方形面积公式计算.
【解答】解:两个阴影图形可以平移组成一个长方形,长为15﹣2=13,宽为8,
故阴影部分的面积=13×8=104.
【点评】本题主要考查平移的性质,把复杂的问题化简单.
20.如图所示,由三角形ABC平移得到的三角形有 5 个.
【分析】平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同,据此判断出由三角形ABC平移得到的三角形有哪些即可.
【解答】解:如图1,,
由三角形ABC平移得到的三角形有5个:
△DBE、△BHI、△EFG、△EIM、△IPN.
故答案为:5.
【点评】此题主要考查了平移的性质和应用,要熟练掌握,解答此题的关键是要明确:①把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.②新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.
三.解答题(共8小题)
21.如图,直线AB、CD、EF相交于点O.
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.
【分析】(1)根据邻补角的概念即可解答;
(2)根据对顶角的概念即可解答;
(3)因为∠BOF=90°,所以AB⊥EF,由此可得∠AOF,再根据对顶角的概念可得∠FOC的度数.
【解答】解:(1)∠COE的邻补角为∠COF和∠EOD;
(2)∠COE和∠BOE的对顶角分别为∠DOF和∠AOF;
(3)∵∠BOF=90°,
∴AB⊥EF
∴∠AOF=90°,
又∵∠AOC=∠BOD=60°
∴∠FOC=∠AOF+∠AOC=90°+60°=150°.
【点评】本题考查的主要内容是邻补角和对顶角的概念,以及角的和差计算,掌握邻补角和对顶角的概念是解题的关键.
22.如图①②所示,将两个相同三角板的两个直角顶点O重合在一起,像图①②那样放置.
(1)若∠BOC=60°,如图①,猜想∠AOD的度数;
(2)若∠BOC=70°,如图②,猜想∠AOD的度数;
(3)猜想∠AOD和∠BOC的关系,并写出理由.
【分析】此题利用余角、周角性质即可求出角的度数.应按照题目的要求,逐步计算.
【解答】解:(1)∵∠AOB=90°,∠BOC=60°,
∴∠AOC=∠AOB﹣∠BOC=90°﹣60°=30°.
又∵∠COD=90°,
∴∠AOD=∠AOC+∠COD
=30°+90°=120°.
(2)∵∠AOB+∠COD+∠BOC+∠AOD=360°,
∠AOB=90°,∠COD=90°,∠BOC=70°,
∴∠AOD=360°﹣∠AOB﹣∠COD﹣∠BOC
=360°﹣90°﹣90°﹣70°=110°.
(3)猜想:∠AOD+∠BOC=180°.
理由:如图①∵∠AOD=∠AOC+∠COD=∠AOC+90°,
∠BOC=∠COD﹣∠BOD=90°﹣∠BOD,∠AOC=∠BOD,
∴∠AOD+∠BOC=180°.
【点评】此题主要考查了学生余角、周角的性质.
23.判断下列命题的真假,若是假命题,举出反例.
(1)若两个角不是对顶角,则这两个角不相等;
(2)若ab=0,则a+b=0.
【分析】分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.
【解答】解:(1)假命题.如:两条直线平行,内错角相等.
(2)假命题.如:a=5和b=0.
【点评】主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
24.如图,有三个论断①∠1=∠2;②∠B=∠D;③∠A=∠C,请从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性.
【分析】根据题意,请从中任选两个作为条件,另一个作为结论构成一个命题,根据平行线的判定和性质及对顶角相等进行证明.
【解答】已知:∠B=∠D,∠A=∠C.
求证:∠1=∠2.
证明:∵∠A=∠C,
∴AB∥CD.
∴∠B=∠BFC.
∵∠B=∠D,
∴∠BFC=∠D.
∴DE∥BF.
∴∠DMN=∠BNM.
∵∠1=∠DMN,∠2=∠BNM,
∴∠1=∠2.
【点评】证明的一般步骤:写出已知,求证,画出图形,再证明.
25.宾馆重新装修后,准备在大厅的主楼梯上铺设一种红地毯,已知这种地毯每平方米售价40元,主楼梯道宽2米,其侧面如图所示,求买地毯至少需要多少元?
【分析】根据题意,结合图形,先把楼梯的横竖向上向左平移,构成一个矩形,再求得其面积,则购买地毯的钱数可求.
【解答】解:如图,利用平移线段,把楼梯的横竖向上向左平移,构成一个矩形,长宽分别为6米,4米,
∴地毯的长度为6+4=10米,地毯的面积为10×2=20平方米,
∴买地毯至少需要20×40=800元.
【点评】本题考查了平移的性质,属于基础应用题,解决此题的关键是要利用平移的知识,把要求的所有线段平移到一条直线上进行计算.
26.如图,直线EF将矩形纸片ABCD分成面积相等的两部分,E、F分别与BC交于点E,与AD交于点F(E,F不与顶点重合),设AB=a,AD=b,BE=x.
(Ⅰ)求证:AF=EC;
(Ⅱ)用剪刀将纸片沿直线EF剪开后,再将纸片ABEF沿AB对称翻折,然后平移拼接在梯形ECDF的下方,使一底边重合,直腰落在边DC的延长线上,拼接后,下方的梯形记作EE′B′C.
(1)求出直线EE′分别经过原矩形的顶点A和顶点D时,所对应的x:b的值;
(2)在直线EE′经过原矩形的一个顶点的情形下,连接BE′,直线BE′与EF是否平行?你若认为平行,请给予证明;你若认为不平行,请你说明当a与b满足什么关系时,它们垂直?
【分析】(Ⅰ)由AB=a,AD=b,BE=x,S梯形ABEF=S梯形CDFE,结合梯形的面积公式可证得AF=EC;
(Ⅱ)(1)根据题意,画出图形,结合梯形的性质求得x:b的值;
(2)直线EE′经过原矩形的顶点D时,可证明四边形BE′EF是平行四边形,则BE′∥EF;当直线EE′经过原矩形的顶点A时,BE′与EF不平行.
【解答】(Ⅰ)证明:∵AB=a,AD=b,BE=x,S梯形ABEF=S梯形CDFE,
∴a(x+AF)=a(EC+b﹣AF),
∴2AF=EC+(b﹣x).
又∵EC=b﹣x,
∴2AF=2EC.
∴AF=EC.
(Ⅱ)解:(1)当直线EE′经过原矩形的顶点D时,如图(一)
∵EC∥E′B′,
∴=,
由EC=b﹣x,E′B′=EB=x,DB′=DC+CB′=2a,
得,
∴x:b=.
当直线E′E经过原矩形的顶点A时,如图(二)
在梯形AE′B′D中,
∵EC∥E′B′,点C是DB′的中点,
∴CE=(AD+E′B′),
即b﹣x=(b+x),
∴x:b=.
(2)如图(一),当直线EE′经过原矩形的顶点D时,BE′∥EF,
证明:连接BF,
∵FD∥BE,FD=BE,
∴四边形FBED是平行四边形,
∴FB∥DE,FB=DE,
又∵EC∥E′B′,点C是DB′的中点,
∴DE=EE′,
∴FB∥EE′,FB=EE′,
∴四边形BE′EF是平行四边形,
∴BE′∥EF.
如图(二),当直线EE′经过原矩形的顶点A时,显然BE′与EF不平行,
设直线EF与BE′交于点G,过点E′作E′M⊥BC于M,则E′M=a,
∵x:b=,
∴EM=BC=b,
若BE′与EF垂直,则有∠GBE+∠BEG=90°,
又∵∠BEG=∠FEC=∠MEE′,∠MEE′+∠ME′E=90°,
∴∠GBE=∠ME′E,
在Rt△BME′中,tan∠E′BM=tan∠GBE==,
在Rt△EME′中,tan∠ME′E==,
∴=.
又∵a>0,b>0,
=,
∴当=时,BE′与EF垂直.
【点评】本题是道根据平移的性质、梯形的性质和平行四边形的性质结合求解的综合题,解题复杂,难度大.考查学生综合运用数学知识的能力.
27.已知△A1B1C1是由△ABC经过平移得到的,其中,A、B、C三点的对应点分别是A1、B1、C1,它们在平面直角坐标系中的坐标如下表所示:
△ABC A(a,0) B(3,0) C(5,5)
△A1B1C1 A1(﹣3,2) B1(﹣1,b) C1(c,7)
(1)观察表中各对应点坐标的变化,并填空:a= 1 ,b= 2 ,c= 1 ;
(2)在如图的平面直角坐标系中画出△ABC及△A1B1C1;
(3)△A1B1C1的面积是 5 .
【分析】(1)根据点B横坐标的变化求出向左平移的距离,根据点C纵坐标的变化得出向上平移的距离即可;
(2)在坐标系内描出各点,再画出△ABC及△A1B1C1即可;
(3)矩形的面积减去两个顶点上三角形的面积即可.
【解答】解:(1)∵B(3,0),B1(﹣1,b),
∴向左平移的距离=3+1=4,
∴a﹣4=﹣3,解得a=1,
5﹣c=4,解得c=1;
∵C(5,5),C1(c,7),
∴向上平移的距离=7﹣5=2,
∴n=0+2=2.
故答案为:1,2,1;
(2)如图△ABC及△A1B1C1即为所求;
(3)由图可知,S△A1B1C1=4×5﹣×4×5﹣×2×4=5.
故答案为:5.
【点评】本题考查的是作图﹣平移变换,先根据题意得出图形平移的方向,再根据图形平移不变性的性质求解是解答此题的关键.
28.把小船ABCD通过平移后到A′B′C′D′的位置,请你根据题中信息,画出平移后的小船位置.
【分析】看旗子的一个对应点是向左移9个格子,再向上移1个格子,那么将小船的四个顶点向左移9个格子,再向上移1个格子即可得到所求的位置.
【解答】解:.
【点评】图形的平移要归结为各顶点的平移;解决本题的关键是得到一对对应点之间的平移规律.
一.选择题(共12小题)
1.平面内三条直线的交点个数可能有( )
A.1个或3个 B.2个或3个
C.1个或2个或3个 D.0个或1个或2个或3个
2.如图,三条直线a、b、c相交于一点,则∠1+∠2+∠3=( )
A.360° B.180° C.120° D.90
3.如图,点O为直线AB上一点,OC⊥OD.如果∠1=35°,那么∠2的度数是( )
A.35° B.45° C.55° D.65°
4.下列语句是命题的是( )
(1)两点之间,线段最短;
(2)如果两个角的和是90度,那么这两个角互余.
(3)请画出两条互相平行的直线;
(4)过直线外一点作已知直线的垂线.
A.(1)(2) B.(3)(4) C.(2)(3) D.(1)(4)
5.下列命题中是假命题的是( )
A.同旁内角互补,两直线平行
B.垂线段最短
C.在同一平面内,过一点有且只有一条直线与已知直线垂直
D.直线外一点到这条直线的垂线段叫做点到直线的距离
6.下列命题中,真命题是( )
A.相等的角是对顶角
B.两条直线被第三条直线所截,同位角相等
C.在同一平面内,垂直于同一条直线的两条直线平行
D.同旁内角互补
7.观察下面图案在A、B、C、D四幅图案中,能通过图案平移得到的是( )
A. B. C. D.
8.图中的小船通过平移后可得到的图案是( )
A. B.
C. D.
9.如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,∠B=90°,AB=8,DH=3,平移距离为4,求阴影部分的面积为( )
A.20 B.24 C.25 D.26
10.如图,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=70°,则( )
A.FG=5,∠G=70° B.EH=5,∠F=70°
C.EF=5,∠F=70° D.EF=5,∠E=70°
11.如图所示的图案分别是大众、奥迪、奔驰、三菱汽车的车标,其中,可以看作由“基本图案”经过平移得到的是( )
A. B.
C. D.
12.下列如图所示的图案,分别是奔驰、奥迪、三菱、大众汽车的车标,其中可以看作由“基本图案”经过平移得到的是( )
A. B.
C. D.
二.填空题(共8小题)
13.三条直线两两相交,最少有 个交点,最多有 个交点.
14.若∠1的对顶角是∠2,∠2的邻补角是∠3,∠3=45°,则∠1的度数为 .
15.“同位角相等”的逆命题是 .
16.命题“全等三角形的对应角相等”的逆命题是 ,这个逆命题是 (填“真”或“假”).
17.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的矩形荷塘上架设小桥.若荷塘周长为280m,且桥宽忽略不计,则小桥总长为 m.
18.在高3米,水平距离为4米的楼梯表面铺地毯,地毯的长度至少需要 米.
19.如图,根据长方形中的数据,计算阴影部分的面积为 .
20.如图所示,由三角形ABC平移得到的三角形有 个.
三.解答题(共8小题)
21.如图,直线AB、CD、EF相交于点O.
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.
22.如图①②所示,将两个相同三角板的两个直角顶点O重合在一起,像图①②那样放置.
(1)若∠BOC=60°,如图①,猜想∠AOD的度数;
(2)若∠BOC=70°,如图②,猜想∠AOD的度数;
(3)猜想∠AOD和∠BOC的关系,并写出理由.
23.判断下列命题的真假,若是假命题,举出反例.
(1)若两个角不是对顶角,则这两个角不相等;
(2)若ab=0,则a+b=0.
24.如图,有三个论断①∠1=∠2;②∠B=∠D;③∠A=∠C,请从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性.
25.宾馆重新装修后,准备在大厅的主楼梯上铺设一种红地毯,已知这种地毯每平方米售价40元,主楼梯道宽2米,其侧面如图所示,求买地毯至少需要多少元?
26.如图,直线EF将矩形纸片ABCD分成面积相等的两部分,E、F分别与BC交于点E,与AD交于点F(E,F不与顶点重合),设AB=a,AD=b,BE=x.
(Ⅰ)求证:AF=EC;
(Ⅱ)用剪刀将纸片沿直线EF剪开后,再将纸片ABEF沿AB对称翻折,然后平移拼接在梯形ECDF的下方,使一底边重合,直腰落在边DC的延长线上,拼接后,下方的梯形记作EE′B′C.
(1)求出直线EE′分别经过原矩形的顶点A和顶点D时,所对应的x:b的值;
(2)在直线EE′经过原矩形的一个顶点的情形下,连接BE′,直线BE′与EF是否平行?你若认为平行,请给予证明;你若认为不平行,请你说明当a与b满足什么关系时,它们垂直?
27.已知△A1B1C1是由△ABC经过平移得到的,其中,A、B、C三点的对应点分别是A1、B1、C1,它们在平面直角坐标系中的坐标如下表所示:
△ABC A(a,0) B(3,0) C(5,5)
△A1B1C1 A1(﹣3,2) B1(﹣1,b) C1(c,7)
(1)观察表中各对应点坐标的变化,并填空:a= ,b= ,c= ;
(2)在如图的平面直角坐标系中画出△ABC及△A1B1C1;
(3)△A1B1C1的面积是 .
28.把小船ABCD通过平移后到A′B′C′D′的位置,请你根据题中信息,画出平移后的小船位置.
2020年冀教新版七年级数学下册《第7章 相交线与平行线》单元测试卷
参考答案与试题解析
一.选择题(共12小题)
1.平面内三条直线的交点个数可能有( )
A.1个或3个 B.2个或3个
C.1个或2个或3个 D.0个或1个或2个或3个
【分析】根据相交线的定义,作出所有可能的图形即可得解.
【解答】解:如图所示,
分别有0个交点,1个交点,2个交点,3个交点,
∴交点个数可能有0个或1个或2个或3个.
故选:D.
【点评】本题考查了相交线的知识,穷举出所有的可能情况并作出图形是解题的关键.
2.如图,三条直线a、b、c相交于一点,则∠1+∠2+∠3=( )
A.360° B.180° C.120° D.90
【分析】利用对顶角相等,可知∠1+∠2+∠3的和是360°的一半.
【解答】解:因为对顶角相等,所以∠1+∠2+∠3=×360°=180°.
故选:B.
【点评】本题考查对顶角的性质,是一个需要熟记的内容.
3.如图,点O为直线AB上一点,OC⊥OD.如果∠1=35°,那么∠2的度数是( )
A.35° B.45° C.55° D.65°
【分析】根据垂线的定义,可得∠COD,根据角的和差,可得答案.
【解答】解:∵OC⊥OD,
∴∠COD=90°.
由角的和差,得
∠2=180°﹣∠COD﹣∠1
=180°﹣90°﹣35°=55°,
故选:C.
【点评】本题考查了垂线的定义,利用垂线的定义是解题关键.
4.下列语句是命题的是( )
(1)两点之间,线段最短;
(2)如果两个角的和是90度,那么这两个角互余.
(3)请画出两条互相平行的直线;
(4)过直线外一点作已知直线的垂线.
A.(1)(2) B.(3)(4) C.(2)(3) D.(1)(4)
【分析】判断一件事情的语句叫命题,命题都由题设和结论两部分组成,依此对四个小题进行逐一分析即可;
【解答】解:(1)两点之间,线段最短符合命题定义,正确;
(2)如果两个角的和是90度,那么这两个角互余,符合命题定义,正确.
(3)请画出两条互相平行的直线只是做了陈述,不是命题,错误;
(4)过直线外一点作已知直线的垂线没有做出判断,不是命题,错误,
故选:A.
【点评】本题考查了命题的概念:一般的,在数学中我们把用语言、符号或式子表达的,可以判断真假的陈述句叫做命题.其中判断为真的语句叫做真命题,判断为假的语句叫做假命题.注意命题是一个能够判断真假的陈述句.
5.下列命题中是假命题的是( )
A.同旁内角互补,两直线平行
B.垂线段最短
C.在同一平面内,过一点有且只有一条直线与已知直线垂直
D.直线外一点到这条直线的垂线段叫做点到直线的距离
【分析】根据平行线的判定对A进行判断;
根据垂线段公理对B进行判断;
根据过一点有且只有一条直线与原直线垂直对C进行判断;
根据点到直线的距离的定义对D进行判断.
【解答】解:A、同旁内角互补,两直线平行,所以A选项为真命题;
B、直线外一点与直线上所有点的连线段中,垂线段最短,所以B选项为真命题;
C、在同一平面内,过一点有且只有一条直线与已知直线垂直,所以C选项为真命题;
D、直线外一点到这条直线的垂线段的长叫做点到直线的距离,所以D选项为假命题.
故选:D.
【点评】本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.
6.下列命题中,真命题是( )
A.相等的角是对顶角
B.两条直线被第三条直线所截,同位角相等
C.在同一平面内,垂直于同一条直线的两条直线平行
D.同旁内角互补
【分析】分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.
【解答】解:A、错误,对顶角相等但相等的角不一定是对顶角;
B、错误,当被截的直线平行时形成的同位角才相等;
C、正确,必须强调在同一平面内;
D、错误,两直线平行同旁内角才互补.
故选:C.
【点评】主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
7.观察下面图案在A、B、C、D四幅图案中,能通过图案平移得到的是( )
A. B. C. D.
【分析】找到平移前后形状与大小没有改变,并且对应点的连线平行且相等的图形即可.
【解答】解:A、对应点的连线相交,不能通过平移得到,不符合题意;
B、对应点的连线相交,不能通过平移得到,不符合题意;
C、可通过平移得到,符合题意;
D、对应点的连线相交,不能通过平移得到,不符合题意;
故选:C.
【点评】本题需抓住平移前后对应点的连线平行且相等这个知识点进行解答.
8.图中的小船通过平移后可得到的图案是( )
A. B.
C. D.
【分析】根据平移的概念:在平面内,把一个图形整体沿某一的方向移动,这种图形的平行移动,叫做平移变换,简称平移可以选出答案.
【解答】解:根据平移定义可得:图中的小船通过平移后可得到的图案是B.
故选:B.
【点评】此题主要考查了生活中的平移,关键是掌握平移是指图形的平行移动,平移时图形中所有点移动的方向一致,并且移动的距离相等.
9.如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,∠B=90°,AB=8,DH=3,平移距离为4,求阴影部分的面积为( )
A.20 B.24 C.25 D.26
【分析】由S△ABC=S△DEF,推出S四边形ABEH=S阴即可解决问题;
【解答】解:∵平移距离为4,
∴BE=4,
∵AB=8,DH=3,
∴EH=8﹣3=5,
∵S△ABC=S△DEF,
∴S四边形ABEH=S阴
∴阴影部分的面积为=×(8+5)×4=26
故选:D.
【点评】此题主要考查了平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等,要熟练掌握.
10.如图,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=70°,则( )
A.FG=5,∠G=70° B.EH=5,∠F=70°
C.EF=5,∠F=70° D.EF=5,∠E=70°
【分析】经过平移,对应线段平行(或共线)且相等,对应角相等,对应点所连接的线段平行且相等.
【解答】解:在四边形EFGH,EH是AD的对应边,∠F是∠B的对应角,
∵AD=5,∠B=70°,故EH=5,∠F=70°.
故选:B.
【点评】解题的关键是利用平移的性质,找准对应边、对应角.
11.如图所示的图案分别是大众、奥迪、奔驰、三菱汽车的车标,其中,可以看作由“基本图案”经过平移得到的是( )
A. B.
C. D.
【分析】根据平移不改变图形的形状和大小,将题中所示的图案通过平移后可以得到的图案是B.
【解答】解:观察图形可知,图案B可以看作由“基本图案”经过平移得到.
故选:B.
【点评】本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转,而误选A、C、D.
12.下列如图所示的图案,分别是奔驰、奥迪、三菱、大众汽车的车标,其中可以看作由“基本图案”经过平移得到的是( )
A. B.
C. D.
【分析】根据平移的性质:不改变图形的形状和大小,不可旋转与翻转,将题中所示的图案通过平移后可以得到的图案是B.
【解答】解:观察图形可知,图案C可以看作由“基本图案”经过平移得到.
故选:B.
【点评】此题主要考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转,而导致错选.
二.填空题(共8小题)
13.三条直线两两相交,最少有 1 个交点,最多有 3 个交点.
【分析】最少的交点个数即其相交于一点,而最多也就能构成一个三角形,即三个交点.
【解答】解:如图所示:
两两相交的直线,其最少有1个交点,即三条直线相交于一点;
最多有三个交点,即其构成一个三角形,共三个交点.
故答案为1,3.
【点评】本题主要考查了相交线,关键是考虑全面,不要漏解.
14.若∠1的对顶角是∠2,∠2的邻补角是∠3,∠3=45°,则∠1的度数为 135° .
【分析】根据对顶角相等、邻补角互补的性质求解.
【解答】解:∵∠2的邻补角是∠3,∠3=45°,
∴∠2=180°﹣∠3=135°.
∵∠1的对顶角是∠2,
∴∠1=∠2=135°.
【点评】本题考查对顶角的性质以及邻补角的定义,是一个需要熟记的内容.
15.“同位角相等”的逆命题是 相等的角是同位角 .
【分析】“同位角相等”的题设为两个角为同位角,结论为这两个角相等,然后交换题设与结论即可得到原命题的逆命题.
【解答】解:“同位角相等”的逆命题为:相等的两个角为同位角.
故答案为:相等的角是同位角.
【点评】本题考查了逆命题,关键找出题设和结论部分,然后交换题设和结论即为逆命题.
16.命题“全等三角形的对应角相等”的逆命题是 对应角相等的三角形是全等三角形 ,这个逆命题是 假 (填“真”或“假”).
【分析】根据逆命题的概念,交换原命题的题设与结论即可的出原命题的逆命题,进而判断它的真假.
【解答】解:命题“全等三角形对应角相等”的题设是“全等三角形”,结论是“对应角相等”,
故其逆命题是对应角相等的三角形是全等三角形,它是一个假命题.
故答案为:对应角相等的三角形是全等三角形,假.
【点评】此题考查了互逆命题的知识,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题.
17.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的矩形荷塘上架设小桥.若荷塘周长为280m,且桥宽忽略不计,则小桥总长为 140 m.
【分析】利用平移的性质直接得出答案即可.
【解答】解:根据题意得出:小桥可以平移到矩形的边上,得出小桥的长等于矩形的长与宽的和,
故小桥总长为:280÷2=140(m).
故答案为:140.
【点评】此题主要考查了生活中的平移,根据已知正确平移小桥是解题关键.
18.在高3米,水平距离为4米的楼梯表面铺地毯,地毯的长度至少需要 7 米.
【分析】把楼梯的水平线段向下平移,竖直线段向右平移可得地毯长度为水平距离与高的和.
【解答】解:地毯长度至少需3+4=7米.
故答案为:7.
【点评】此题主要考查了生活中的平移及平移的性质,根据已知得出地毯的长度应等于水平距离与高的和是解题关键.
19.如图,根据长方形中的数据,计算阴影部分的面积为 104 .
【分析】两个阴影图形可以平移到一个长方形中去,故根据长方形面积公式计算.
【解答】解:两个阴影图形可以平移组成一个长方形,长为15﹣2=13,宽为8,
故阴影部分的面积=13×8=104.
【点评】本题主要考查平移的性质,把复杂的问题化简单.
20.如图所示,由三角形ABC平移得到的三角形有 5 个.
【分析】平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同,据此判断出由三角形ABC平移得到的三角形有哪些即可.
【解答】解:如图1,,
由三角形ABC平移得到的三角形有5个:
△DBE、△BHI、△EFG、△EIM、△IPN.
故答案为:5.
【点评】此题主要考查了平移的性质和应用,要熟练掌握,解答此题的关键是要明确:①把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.②新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.
三.解答题(共8小题)
21.如图,直线AB、CD、EF相交于点O.
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.
【分析】(1)根据邻补角的概念即可解答;
(2)根据对顶角的概念即可解答;
(3)因为∠BOF=90°,所以AB⊥EF,由此可得∠AOF,再根据对顶角的概念可得∠FOC的度数.
【解答】解:(1)∠COE的邻补角为∠COF和∠EOD;
(2)∠COE和∠BOE的对顶角分别为∠DOF和∠AOF;
(3)∵∠BOF=90°,
∴AB⊥EF
∴∠AOF=90°,
又∵∠AOC=∠BOD=60°
∴∠FOC=∠AOF+∠AOC=90°+60°=150°.
【点评】本题考查的主要内容是邻补角和对顶角的概念,以及角的和差计算,掌握邻补角和对顶角的概念是解题的关键.
22.如图①②所示,将两个相同三角板的两个直角顶点O重合在一起,像图①②那样放置.
(1)若∠BOC=60°,如图①,猜想∠AOD的度数;
(2)若∠BOC=70°,如图②,猜想∠AOD的度数;
(3)猜想∠AOD和∠BOC的关系,并写出理由.
【分析】此题利用余角、周角性质即可求出角的度数.应按照题目的要求,逐步计算.
【解答】解:(1)∵∠AOB=90°,∠BOC=60°,
∴∠AOC=∠AOB﹣∠BOC=90°﹣60°=30°.
又∵∠COD=90°,
∴∠AOD=∠AOC+∠COD
=30°+90°=120°.
(2)∵∠AOB+∠COD+∠BOC+∠AOD=360°,
∠AOB=90°,∠COD=90°,∠BOC=70°,
∴∠AOD=360°﹣∠AOB﹣∠COD﹣∠BOC
=360°﹣90°﹣90°﹣70°=110°.
(3)猜想:∠AOD+∠BOC=180°.
理由:如图①∵∠AOD=∠AOC+∠COD=∠AOC+90°,
∠BOC=∠COD﹣∠BOD=90°﹣∠BOD,∠AOC=∠BOD,
∴∠AOD+∠BOC=180°.
【点评】此题主要考查了学生余角、周角的性质.
23.判断下列命题的真假,若是假命题,举出反例.
(1)若两个角不是对顶角,则这两个角不相等;
(2)若ab=0,则a+b=0.
【分析】分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.
【解答】解:(1)假命题.如:两条直线平行,内错角相等.
(2)假命题.如:a=5和b=0.
【点评】主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
24.如图,有三个论断①∠1=∠2;②∠B=∠D;③∠A=∠C,请从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性.
【分析】根据题意,请从中任选两个作为条件,另一个作为结论构成一个命题,根据平行线的判定和性质及对顶角相等进行证明.
【解答】已知:∠B=∠D,∠A=∠C.
求证:∠1=∠2.
证明:∵∠A=∠C,
∴AB∥CD.
∴∠B=∠BFC.
∵∠B=∠D,
∴∠BFC=∠D.
∴DE∥BF.
∴∠DMN=∠BNM.
∵∠1=∠DMN,∠2=∠BNM,
∴∠1=∠2.
【点评】证明的一般步骤:写出已知,求证,画出图形,再证明.
25.宾馆重新装修后,准备在大厅的主楼梯上铺设一种红地毯,已知这种地毯每平方米售价40元,主楼梯道宽2米,其侧面如图所示,求买地毯至少需要多少元?
【分析】根据题意,结合图形,先把楼梯的横竖向上向左平移,构成一个矩形,再求得其面积,则购买地毯的钱数可求.
【解答】解:如图,利用平移线段,把楼梯的横竖向上向左平移,构成一个矩形,长宽分别为6米,4米,
∴地毯的长度为6+4=10米,地毯的面积为10×2=20平方米,
∴买地毯至少需要20×40=800元.
【点评】本题考查了平移的性质,属于基础应用题,解决此题的关键是要利用平移的知识,把要求的所有线段平移到一条直线上进行计算.
26.如图,直线EF将矩形纸片ABCD分成面积相等的两部分,E、F分别与BC交于点E,与AD交于点F(E,F不与顶点重合),设AB=a,AD=b,BE=x.
(Ⅰ)求证:AF=EC;
(Ⅱ)用剪刀将纸片沿直线EF剪开后,再将纸片ABEF沿AB对称翻折,然后平移拼接在梯形ECDF的下方,使一底边重合,直腰落在边DC的延长线上,拼接后,下方的梯形记作EE′B′C.
(1)求出直线EE′分别经过原矩形的顶点A和顶点D时,所对应的x:b的值;
(2)在直线EE′经过原矩形的一个顶点的情形下,连接BE′,直线BE′与EF是否平行?你若认为平行,请给予证明;你若认为不平行,请你说明当a与b满足什么关系时,它们垂直?
【分析】(Ⅰ)由AB=a,AD=b,BE=x,S梯形ABEF=S梯形CDFE,结合梯形的面积公式可证得AF=EC;
(Ⅱ)(1)根据题意,画出图形,结合梯形的性质求得x:b的值;
(2)直线EE′经过原矩形的顶点D时,可证明四边形BE′EF是平行四边形,则BE′∥EF;当直线EE′经过原矩形的顶点A时,BE′与EF不平行.
【解答】(Ⅰ)证明:∵AB=a,AD=b,BE=x,S梯形ABEF=S梯形CDFE,
∴a(x+AF)=a(EC+b﹣AF),
∴2AF=EC+(b﹣x).
又∵EC=b﹣x,
∴2AF=2EC.
∴AF=EC.
(Ⅱ)解:(1)当直线EE′经过原矩形的顶点D时,如图(一)
∵EC∥E′B′,
∴=,
由EC=b﹣x,E′B′=EB=x,DB′=DC+CB′=2a,
得,
∴x:b=.
当直线E′E经过原矩形的顶点A时,如图(二)
在梯形AE′B′D中,
∵EC∥E′B′,点C是DB′的中点,
∴CE=(AD+E′B′),
即b﹣x=(b+x),
∴x:b=.
(2)如图(一),当直线EE′经过原矩形的顶点D时,BE′∥EF,
证明:连接BF,
∵FD∥BE,FD=BE,
∴四边形FBED是平行四边形,
∴FB∥DE,FB=DE,
又∵EC∥E′B′,点C是DB′的中点,
∴DE=EE′,
∴FB∥EE′,FB=EE′,
∴四边形BE′EF是平行四边形,
∴BE′∥EF.
如图(二),当直线EE′经过原矩形的顶点A时,显然BE′与EF不平行,
设直线EF与BE′交于点G,过点E′作E′M⊥BC于M,则E′M=a,
∵x:b=,
∴EM=BC=b,
若BE′与EF垂直,则有∠GBE+∠BEG=90°,
又∵∠BEG=∠FEC=∠MEE′,∠MEE′+∠ME′E=90°,
∴∠GBE=∠ME′E,
在Rt△BME′中,tan∠E′BM=tan∠GBE==,
在Rt△EME′中,tan∠ME′E==,
∴=.
又∵a>0,b>0,
=,
∴当=时,BE′与EF垂直.
【点评】本题是道根据平移的性质、梯形的性质和平行四边形的性质结合求解的综合题,解题复杂,难度大.考查学生综合运用数学知识的能力.
27.已知△A1B1C1是由△ABC经过平移得到的,其中,A、B、C三点的对应点分别是A1、B1、C1,它们在平面直角坐标系中的坐标如下表所示:
△ABC A(a,0) B(3,0) C(5,5)
△A1B1C1 A1(﹣3,2) B1(﹣1,b) C1(c,7)
(1)观察表中各对应点坐标的变化,并填空:a= 1 ,b= 2 ,c= 1 ;
(2)在如图的平面直角坐标系中画出△ABC及△A1B1C1;
(3)△A1B1C1的面积是 5 .
【分析】(1)根据点B横坐标的变化求出向左平移的距离,根据点C纵坐标的变化得出向上平移的距离即可;
(2)在坐标系内描出各点,再画出△ABC及△A1B1C1即可;
(3)矩形的面积减去两个顶点上三角形的面积即可.
【解答】解:(1)∵B(3,0),B1(﹣1,b),
∴向左平移的距离=3+1=4,
∴a﹣4=﹣3,解得a=1,
5﹣c=4,解得c=1;
∵C(5,5),C1(c,7),
∴向上平移的距离=7﹣5=2,
∴n=0+2=2.
故答案为:1,2,1;
(2)如图△ABC及△A1B1C1即为所求;
(3)由图可知,S△A1B1C1=4×5﹣×4×5﹣×2×4=5.
故答案为:5.
【点评】本题考查的是作图﹣平移变换,先根据题意得出图形平移的方向,再根据图形平移不变性的性质求解是解答此题的关键.
28.把小船ABCD通过平移后到A′B′C′D′的位置,请你根据题中信息,画出平移后的小船位置.
【分析】看旗子的一个对应点是向左移9个格子,再向上移1个格子,那么将小船的四个顶点向左移9个格子,再向上移1个格子即可得到所求的位置.
【解答】解:.
【点评】图形的平移要归结为各顶点的平移;解决本题的关键是得到一对对应点之间的平移规律.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
