六年级上册数学试题-第四单元达标作业 冀教版(含答案)
文档属性
| 名称 | 六年级上册数学试题-第四单元达标作业 冀教版(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 327.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 16:01:06 | ||
图片预览


文档简介
第四单元达标作业
一、仔细想,认真填。
1.在一个比例中,两个内项的积是15.4,一个外项是0.7,另一个外项是( )。
2.农田施肥总量一定,施肥的公顷数和每公顷农田施肥量成( )比例关系。同等价钱的水杯,买水杯的个数和需要的钱数成( )比例关系。
3.如果(a、b均不为0),那么a:b=( ):( )。
4.km这是( )比例尺。图上1 cm表示实际( )km,改写成数值比例尺( )。
5.一个长5 cm、宽3 cm的长方形按3:1放大,得到的图形的面积是( )cm2。
二、精挑细选。(将正确答案的序号填在括号里)
1.能与组成比例的是( )。
A.7:8
B.8:7
14:16
2.如果把圆的半径按1:2缩小,那么新的圆和原来的圆的面积比是( )。
A.2:1
B.1:2
C.1:4
D.4:1
3.全班人数一定,出勤人数和出勤率( )。
A.成正比例关系
B.成反比例关系
C.不成比例
D.无法确定
4.一根木料锯成5段要用16分钟,照这样计算,把这根木料锯成10段要用多长时间?如果设需要用的时间为x分钟,用比例解,列式正确的是( )。
A.
B.
C.
D.
三、解比例。
5.4:1.8=x:15
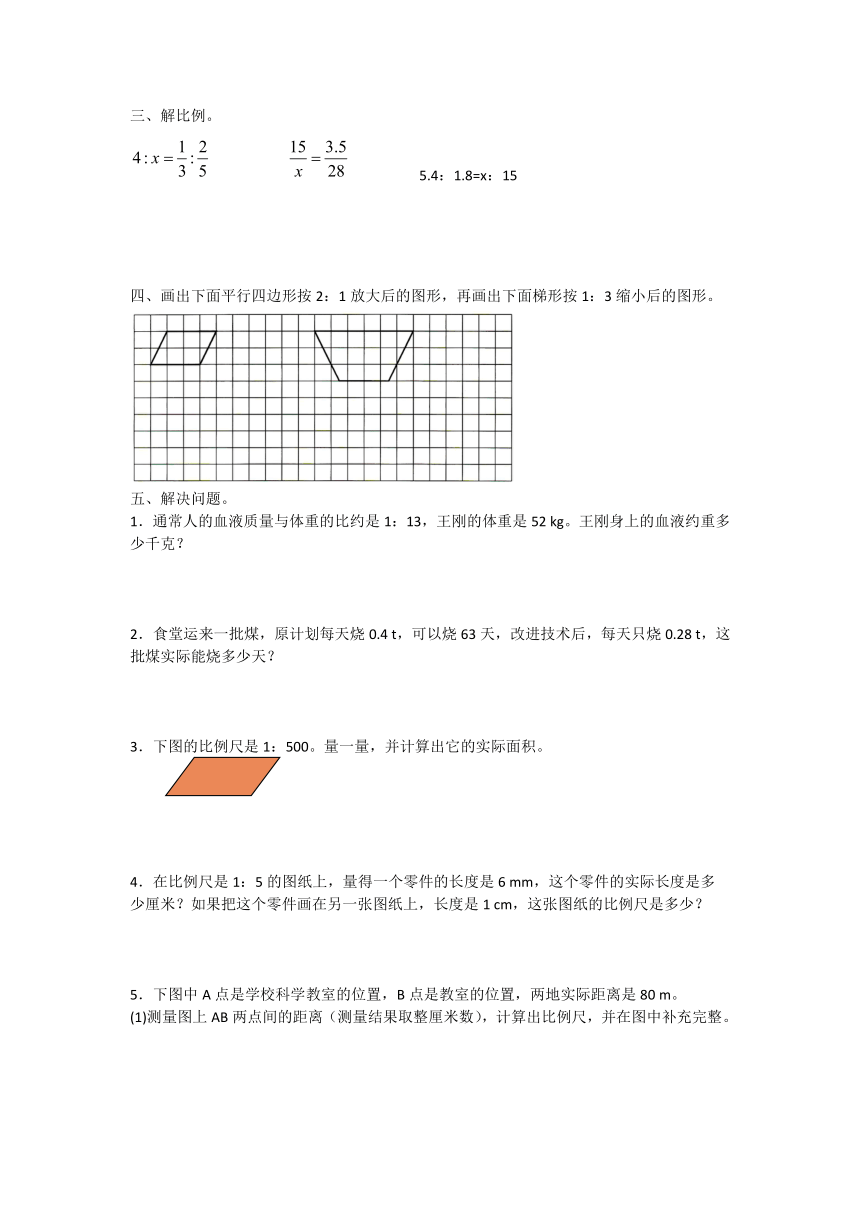
四、画出下面平行四边形按2:1放大后的图形,再画出下面梯形按1:3缩小后的图形。
五、解决问题。
1.通常人的血液质量与体重的比约是1:13,王刚的体重是52 kg。王刚身上的血液约重多少千克?
食堂运来一批煤,原计划每天烧0.4 t,可以烧63天,改进技术后,每天只烧0.28 t,这批煤实际能烧多少天?
3.下图的比例尺是1:500。量一量,并计算出它的实际面积。
4.在比例尺是1:5的图纸上,量得一个零件的长度是6 mm,这个零件的实际长度是多
少厘米?如果把这个零件画在另一张图纸上,长度是1 cm,这张图纸的比例尺是多少?
5.下图中A点是学校科学教室的位置,B点是教室的位置,两地实际距离是80 m。
(1)测量图上AB两点间的距离(测量结果取整厘米数),计算出比例尺,并在图中补充完整。
图书馆在教室北偏东30°距离教室100 m的位置上,请在网中用★标出图书馆的位置。
6.一个榨油厂用80 kg油菜籽可榨油32 kg,照这样计算。
(1)120 t油菜籽可榨油多少吨? (2)如果要榨油25.2 t,需要多少吨油菜籽?
第四单元达标作业
一、1. 22
解析 根据比例的基本性质可知,因为两个内项的积是15.4,所以两个外项的积也是15.4。其中一个外项是0.7,另一个外项为15.4÷0.7=22。
2.反 正
解析 农田施肥总量一定,施肥的公顷数与每公顷农田施肥量的乘积一定,两种量成反比例关系。水杯的单价相同,买水杯需要的钱数和水杯个数的比值一定,两种量成正比例关系。
3. 3(或1 6)
解析 根据比例的基本性质,可知。
4.线段 30 1:3000000
解析 线段比例尺改写成数值比例尺,需要把单位“km”换算成“cm”。1 cm:30 km=1 cm:3000000 cm =1:3000000。
5. 135
解析 长方形的长和宽按3:1放大,则放大后的图形长为15 cm,宽为9 cm,其面积为15×9=135(cm2)。
二、1.B
解析 假设与四个选项中的比都可以组成比例,计算组成的比例的内项之积和外项之积是否相等,若相等,则可以组成比例,反之则不能。
2.C
解析 假设原来圆的半径为r,则面积可表示为πr2。半径按1:2缩小后是r,面积可表示为。所以新圆面积与原来圆面积之比为。
3.A
解析 根据“”可得“”,已知全班人数一定,所以出勤人数和出勤率的比值一定,两种量成正比例关系。
4.C
解析 木料锯成5段,锯的次数是5-1=4,锯成10段,锯的次数是10-1=9。木料锯一次用的时间相等,锯的次数与所用总时间成正比例关系。由此可列出比例关系式:。
三、
解: 解:3.5x=15×28
3.5x=420
x=120
5.4 : 1.8=x : 15
解: 1.8x =5.4×15
1.8x= 81
x=45
解析 根据比例的基本性质求解即可。
四、
解析假设每小格边长为1,则原平行四边形的上、下边的长均为3,按2:1放大后都变为3×2=6,原平行四边形的高为2,按2:1放大后变为2×2=4,画出的平行四边形底是6、高是4且形状与原平行四边形相同。原梯形的上、下底的长分别为3、6,按1:3缩小后变为3÷3 =1、6÷3=2,原梯形的高为3,按1:3缩小后变为3÷3 =1,据此画出上、下底分别是1、2,高是1的梯形,且形状与原梯形相同。
五、1.解:设王刚身上的血液约重x kg。
13x=1×52
x=4
答:王刚身上的血液约重4 kg。
解析 根据题意可知,人的血液质量与体重成正比例关系,由此可列出比例:。
2.解:设这批煤实际能烧x天。
63×0.4=0.28x
0.28x=25.2
x= 90
答:这批煤实际能烧90天。
解析 这批煤的总量一定,每天烧的吨数与所烧天数成反比例关系,也就是说,每天烧的吨数与所烧天数的乘积一定。由此设这批煤实际能烧x天,可列出方程63×0.4=0.28x。
3.测量得:图中平行四边形的底为3 cm、高为1.5 cm。
解:设平行四边形的实际底为x cm,高为ycm。
x=3×500 y=1.5×500
x=1500 y=750
1500cm=15m
750cm=7.5m
15×7.5 =112.5( m2)
答:它的实际面积为112.5 m2。
解析根据“”,可以设平行四边形的实际底、高分别为x cm、y cm,列出比例:,,可以求得平行四边形的实际底、高。根据平行四边形的面积公式求面积。
4.解:设这个零件的实际长度是x mm。
x=5×6
x=30
30 mm=3 cm
答:这个零件的实际长度是3 cm。
1 cm:3 cm=1:3
答:这张图纸的比例尺是1:3。
解析 根据“”,可以设这个零件的实际长度是x mm,列出比例:,求得零件的实际长度为30 mm。根据零件的实际长度和新图纸上的图上长度,求得新图纸的比例尺。
5.(1)测量得图上AB两点间的距离为2 cm。
80 m=8000 cm
2 cm:8000 cm=1:4000
(比例尺见(2)题图)
解析 通过测量可知图上AB两点间的距离是2 cm,根据“”,可以计算出比例尺为1: 4000。
(2)100 m=10000 cm
图书馆的图上距离为:10000×=2.5( cm)
如图所示。
解析 根据“”,推出“图上距离=实际距离×比例尺”,得出图书馆与教室的图上距离为2.5 cm。利用量角器确定北偏东30°的方向后测量出2.5 cm长度用★记为图书馆的位置。
6.(1)解:设120 t油菜籽可榨油x t。
80x=32×120
80x=3840
x =48
答:120 t油菜籽可榨油48 t。
解析 因为油菜籽的出油率一定,所以菜籽油的质量和油菜籽的质量成正比例关系。也就是说菜籽油的质量和油菜籽的质量的比值一定,由此可列出比例:
(2)解:设需要y t油菜籽。
32y=25.2×80
32y=2016
y=63
答:需要63 t油菜籽。
解析 因为油菜籽的出油率一定,所以菜籽油的质量和油菜籽的质量成正比例关系。也就是说菜籽油的质量和油菜籽的质量的比值一定,由此可列出比例:。
一、仔细想,认真填。
1.在一个比例中,两个内项的积是15.4,一个外项是0.7,另一个外项是( )。
2.农田施肥总量一定,施肥的公顷数和每公顷农田施肥量成( )比例关系。同等价钱的水杯,买水杯的个数和需要的钱数成( )比例关系。
3.如果(a、b均不为0),那么a:b=( ):( )。
4.km这是( )比例尺。图上1 cm表示实际( )km,改写成数值比例尺( )。
5.一个长5 cm、宽3 cm的长方形按3:1放大,得到的图形的面积是( )cm2。
二、精挑细选。(将正确答案的序号填在括号里)
1.能与组成比例的是( )。
A.7:8
B.8:7
14:16
2.如果把圆的半径按1:2缩小,那么新的圆和原来的圆的面积比是( )。
A.2:1
B.1:2
C.1:4
D.4:1
3.全班人数一定,出勤人数和出勤率( )。
A.成正比例关系
B.成反比例关系
C.不成比例
D.无法确定
4.一根木料锯成5段要用16分钟,照这样计算,把这根木料锯成10段要用多长时间?如果设需要用的时间为x分钟,用比例解,列式正确的是( )。
A.
B.
C.
D.
三、解比例。
5.4:1.8=x:15
四、画出下面平行四边形按2:1放大后的图形,再画出下面梯形按1:3缩小后的图形。
五、解决问题。
1.通常人的血液质量与体重的比约是1:13,王刚的体重是52 kg。王刚身上的血液约重多少千克?
食堂运来一批煤,原计划每天烧0.4 t,可以烧63天,改进技术后,每天只烧0.28 t,这批煤实际能烧多少天?
3.下图的比例尺是1:500。量一量,并计算出它的实际面积。
4.在比例尺是1:5的图纸上,量得一个零件的长度是6 mm,这个零件的实际长度是多
少厘米?如果把这个零件画在另一张图纸上,长度是1 cm,这张图纸的比例尺是多少?
5.下图中A点是学校科学教室的位置,B点是教室的位置,两地实际距离是80 m。
(1)测量图上AB两点间的距离(测量结果取整厘米数),计算出比例尺,并在图中补充完整。
图书馆在教室北偏东30°距离教室100 m的位置上,请在网中用★标出图书馆的位置。
6.一个榨油厂用80 kg油菜籽可榨油32 kg,照这样计算。
(1)120 t油菜籽可榨油多少吨? (2)如果要榨油25.2 t,需要多少吨油菜籽?
第四单元达标作业
一、1. 22
解析 根据比例的基本性质可知,因为两个内项的积是15.4,所以两个外项的积也是15.4。其中一个外项是0.7,另一个外项为15.4÷0.7=22。
2.反 正
解析 农田施肥总量一定,施肥的公顷数与每公顷农田施肥量的乘积一定,两种量成反比例关系。水杯的单价相同,买水杯需要的钱数和水杯个数的比值一定,两种量成正比例关系。
3. 3(或1 6)
解析 根据比例的基本性质,可知。
4.线段 30 1:3000000
解析 线段比例尺改写成数值比例尺,需要把单位“km”换算成“cm”。1 cm:30 km=1 cm:3000000 cm =1:3000000。
5. 135
解析 长方形的长和宽按3:1放大,则放大后的图形长为15 cm,宽为9 cm,其面积为15×9=135(cm2)。
二、1.B
解析 假设与四个选项中的比都可以组成比例,计算组成的比例的内项之积和外项之积是否相等,若相等,则可以组成比例,反之则不能。
2.C
解析 假设原来圆的半径为r,则面积可表示为πr2。半径按1:2缩小后是r,面积可表示为。所以新圆面积与原来圆面积之比为。
3.A
解析 根据“”可得“”,已知全班人数一定,所以出勤人数和出勤率的比值一定,两种量成正比例关系。
4.C
解析 木料锯成5段,锯的次数是5-1=4,锯成10段,锯的次数是10-1=9。木料锯一次用的时间相等,锯的次数与所用总时间成正比例关系。由此可列出比例关系式:。
三、
解: 解:3.5x=15×28
3.5x=420
x=120
5.4 : 1.8=x : 15
解: 1.8x =5.4×15
1.8x= 81
x=45
解析 根据比例的基本性质求解即可。
四、
解析假设每小格边长为1,则原平行四边形的上、下边的长均为3,按2:1放大后都变为3×2=6,原平行四边形的高为2,按2:1放大后变为2×2=4,画出的平行四边形底是6、高是4且形状与原平行四边形相同。原梯形的上、下底的长分别为3、6,按1:3缩小后变为3÷3 =1、6÷3=2,原梯形的高为3,按1:3缩小后变为3÷3 =1,据此画出上、下底分别是1、2,高是1的梯形,且形状与原梯形相同。
五、1.解:设王刚身上的血液约重x kg。
13x=1×52
x=4
答:王刚身上的血液约重4 kg。
解析 根据题意可知,人的血液质量与体重成正比例关系,由此可列出比例:。
2.解:设这批煤实际能烧x天。
63×0.4=0.28x
0.28x=25.2
x= 90
答:这批煤实际能烧90天。
解析 这批煤的总量一定,每天烧的吨数与所烧天数成反比例关系,也就是说,每天烧的吨数与所烧天数的乘积一定。由此设这批煤实际能烧x天,可列出方程63×0.4=0.28x。
3.测量得:图中平行四边形的底为3 cm、高为1.5 cm。
解:设平行四边形的实际底为x cm,高为ycm。
x=3×500 y=1.5×500
x=1500 y=750
1500cm=15m
750cm=7.5m
15×7.5 =112.5( m2)
答:它的实际面积为112.5 m2。
解析根据“”,可以设平行四边形的实际底、高分别为x cm、y cm,列出比例:,,可以求得平行四边形的实际底、高。根据平行四边形的面积公式求面积。
4.解:设这个零件的实际长度是x mm。
x=5×6
x=30
30 mm=3 cm
答:这个零件的实际长度是3 cm。
1 cm:3 cm=1:3
答:这张图纸的比例尺是1:3。
解析 根据“”,可以设这个零件的实际长度是x mm,列出比例:,求得零件的实际长度为30 mm。根据零件的实际长度和新图纸上的图上长度,求得新图纸的比例尺。
5.(1)测量得图上AB两点间的距离为2 cm。
80 m=8000 cm
2 cm:8000 cm=1:4000
(比例尺见(2)题图)
解析 通过测量可知图上AB两点间的距离是2 cm,根据“”,可以计算出比例尺为1: 4000。
(2)100 m=10000 cm
图书馆的图上距离为:10000×=2.5( cm)
如图所示。
解析 根据“”,推出“图上距离=实际距离×比例尺”,得出图书馆与教室的图上距离为2.5 cm。利用量角器确定北偏东30°的方向后测量出2.5 cm长度用★记为图书馆的位置。
6.(1)解:设120 t油菜籽可榨油x t。
80x=32×120
80x=3840
x =48
答:120 t油菜籽可榨油48 t。
解析 因为油菜籽的出油率一定,所以菜籽油的质量和油菜籽的质量成正比例关系。也就是说菜籽油的质量和油菜籽的质量的比值一定,由此可列出比例:
(2)解:设需要y t油菜籽。
32y=25.2×80
32y=2016
y=63
答:需要63 t油菜籽。
解析 因为油菜籽的出油率一定,所以菜籽油的质量和油菜籽的质量成正比例关系。也就是说菜籽油的质量和油菜籽的质量的比值一定,由此可列出比例:。
