沪科版九年级数学下册课件26.2.2用画树状图法或列表法求概率(19张)
文档属性
| 名称 | 沪科版九年级数学下册课件26.2.2用画树状图法或列表法求概率(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-07 00:00:00 | ||
图片预览





文档简介
课件19张PPT。第二十六章
概率初步九年级数学沪科版·下册26.2.2用画树状图法或列表法求概率教学目标1.进一步理解等可能事件概率的意义.
2.学习运用树形图计算事件的概率.
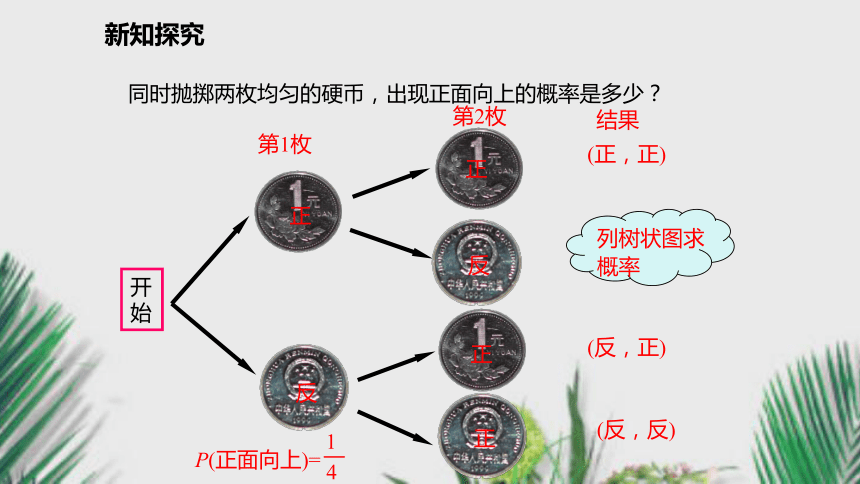
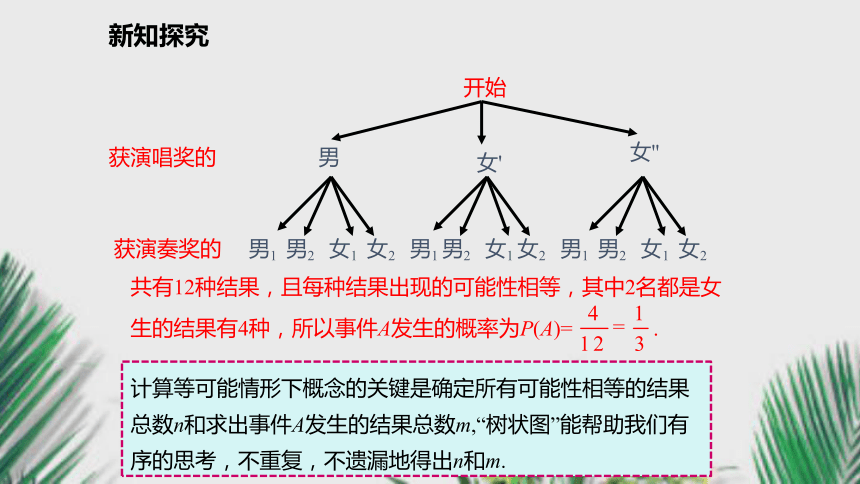
3.进一步学习分类思想方法,掌握有关数学技能.情景导入问题引入现有A,B,C三盘包子,已知A盘中有两个酸菜包和一个糖包,B盘中有一个酸菜包和一个糖包和一个韭菜包,C盘中有一个酸菜包和一个糖包以及一个馒头.老师就爱吃酸菜包.如果老师从每个盘中各选一个包子(馒头除外),那么老师选的包子全部是酸菜包的概率是多少?新知探究互动探究问题1 抛掷一枚均匀的硬币,出现正面向上的概率是多少? P(正面向上)=问题2 同时抛掷两枚均匀的硬币,出现正面向上的概率是多少? 可能出现的结果有(正,正)(正,反)(反,正)(反,反)P(正面向上)=新知探究 同时抛掷两枚均匀的硬币,出现正面向上的概率是多少? 开始第2枚第1枚正反正反正正结果(反,反)(正,正)(正,反)(反,正)P(正面向上)=新知探究典例精析例1 某班有1名男生,2名女生在校文艺演出中获演唱奖,另有2名男生、2名女生获演奏奖.从获演唱奖和演奏奖的学生中各任选1人去领奖,求2人都是女生的概率.解:设2名领奖学生都是女生的事件为A,两种奖项各任选1人的结果用“树状图”来表示.新知探究开始获演唱奖的获演奏奖的男女''女'女1男2男1女2女1男2男1女1男2男1女2女2共有12种结果,且每种结果出现的可能性相等,其中2名都是女生的结果有4种,所以事件A发生的概率为P(A)= .计算等可能情形下概念的关键是确定所有可能性相等的结果总数n和求出事件A发生的结果总数m,“树状图”能帮助我们有序的思考,不重复,不遗漏地得出n和m.新知探究画树形图求概率的基本步骤(1)明确一次试验的几个步骤及顺序;
(2)画树形图列举一次试验的所有可能结果;
(3)数出随机事件A包含的结果数m,试验的所有可能结果数n;
(4)用概率公式进行计算.方法归纳新知探究不一定一样长,只有在距离路灯的距离相等时候影子才会一样长.例2 甲、乙、丙三个盒中分别装有大小、形状、质地相同的小球若干,甲盒中装有2个小球,分别写有字母A和B;乙盒中装有3个小球,分别写有字母C,D和E;丙盒中装有2个小球,分别写有字母H和I;现要从3个盒中各随机取出1个小球.IHAB新知探究(1)取出的3个小球中恰好有1个,2个,3个写有元音字母的概率各是多少?甲乙丙ACDEHIHIHIBCDEHIHIHI解:由树状图得,所有可能出现的结果有12种,它们出现的可能性相等.(1)满足只有一个元音字母的结果有5种,则 P(一个元音)=满足三个全部为元音字母的结果有1种,则 P(三个元音)=满足只有两个元音字母的结果有4种,则 P(两个元音)= =新知探究(2)取出的3个小球上全是辅音字母的概率是多少?甲乙丙ACDEHIHIHIBCDEHIHIHI用树状图列举的结果看起来一目了然,当事件要经过多个(三个或三个以上)步骤完成时,用树状图法求事件的概率很有效.解:满足全是辅音字母的结果有2种,则
P(三个辅音)= = .新知探究经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件发生的概率:
(1)三辆车全部继续直行;
(2)两车向右,一车向左;
(3)至少两车向左.新知探究第一辆左右左右左直右第二辆第三辆直直左右直左右直左直右左直右左直右左直右左直右左直右左直右左直右共有27种行驶方向(2)P(两车向右,一车向左)= ;
(3) P(至少两车向左)= (1)P(全部直行)新知探究现有A,B,C三盘包子,已知A盘中有两个酸菜包和一个糖包,B盘中有一个酸菜包和一个糖包和一个韭菜包,C盘中有一个酸菜包和一个糖包以及一个馒头.老师就爱吃酸菜包.如果老师从每个盘中各选一个包子(馒头除外),那么老师选的包子全部是酸菜包的概率是多少?新知探究解:根据题意,画出树状图如下 由树状图得所有可能出现的结果有18种,它们出现的可能性相等.选的包子全部是酸菜包有2种,所以选的包子全部是酸菜包的概率是课堂小结树状图步骤用法是一种解决试验有多步(或涉及多个因素)的好方法.注意弄清试验涉及试验因素个数或试验步骤分几步;③利用概率公式进行计算.①关键要弄清楚每一步有几种结果;②在树状图下面对应写着所有可能
的结果;②在摸球试验一定要弄清“放回”还
是“不放回”.课堂小测1.a,b,c,d四本不同的书放入一个书包,至少放一本,最多放2本,共有 种不同的放法.2.三女一男四人同行,从中任意选出两人,其性别不同的概率为( )3.在一个不透明的布袋中装有2个白球和n个黄球,它们除颜色外,其余均相同,若从中随机摸出一个球,摸到黄球的概率为 ,则n= .
10C8A. B. C. D. 课堂小测4.在一个不透明的盒子里,装有三个分别写有数字6,-2,7的小球,它们的形状,大小,质地等完全相同.先从盒子里随机取出一个小球,记下数字后放回盒子里,摇匀后再随机取出一个小球,记下数字.请你用列表或画树形图的方法求下列事件发生的概率.
(1)两次取出的小球上的数字相同;
(2)两次取出的小球上的数字之和大于10.课堂小测(1)两次取出的小球上的数字相同的可能性只有3种,所以P(数字相同)=(2)两次取出的小球上的数字之和大于10的可能性只有4种,所以P(数字之和大于10)=解:根据题意,画出树状图如下
2.学习运用树形图计算事件的概率.
3.进一步学习分类思想方法,掌握有关数学技能.情景导入问题引入现有A,B,C三盘包子,已知A盘中有两个酸菜包和一个糖包,B盘中有一个酸菜包和一个糖包和一个韭菜包,C盘中有一个酸菜包和一个糖包以及一个馒头.老师就爱吃酸菜包.如果老师从每个盘中各选一个包子(馒头除外),那么老师选的包子全部是酸菜包的概率是多少?新知探究互动探究问题1 抛掷一枚均匀的硬币,出现正面向上的概率是多少? P(正面向上)=问题2 同时抛掷两枚均匀的硬币,出现正面向上的概率是多少? 可能出现的结果有(正,正)(正,反)(反,正)(反,反)P(正面向上)=新知探究 同时抛掷两枚均匀的硬币,出现正面向上的概率是多少? 开始第2枚第1枚正反正反正正结果(反,反)(正,正)(正,反)(反,正)P(正面向上)=新知探究典例精析例1 某班有1名男生,2名女生在校文艺演出中获演唱奖,另有2名男生、2名女生获演奏奖.从获演唱奖和演奏奖的学生中各任选1人去领奖,求2人都是女生的概率.解:设2名领奖学生都是女生的事件为A,两种奖项各任选1人的结果用“树状图”来表示.新知探究开始获演唱奖的获演奏奖的男女''女'女1男2男1女2女1男2男1女1男2男1女2女2共有12种结果,且每种结果出现的可能性相等,其中2名都是女生的结果有4种,所以事件A发生的概率为P(A)= .计算等可能情形下概念的关键是确定所有可能性相等的结果总数n和求出事件A发生的结果总数m,“树状图”能帮助我们有序的思考,不重复,不遗漏地得出n和m.新知探究画树形图求概率的基本步骤(1)明确一次试验的几个步骤及顺序;
(2)画树形图列举一次试验的所有可能结果;
(3)数出随机事件A包含的结果数m,试验的所有可能结果数n;
(4)用概率公式进行计算.方法归纳新知探究不一定一样长,只有在距离路灯的距离相等时候影子才会一样长.例2 甲、乙、丙三个盒中分别装有大小、形状、质地相同的小球若干,甲盒中装有2个小球,分别写有字母A和B;乙盒中装有3个小球,分别写有字母C,D和E;丙盒中装有2个小球,分别写有字母H和I;现要从3个盒中各随机取出1个小球.IHAB新知探究(1)取出的3个小球中恰好有1个,2个,3个写有元音字母的概率各是多少?甲乙丙ACDEHIHIHIBCDEHIHIHI解:由树状图得,所有可能出现的结果有12种,它们出现的可能性相等.(1)满足只有一个元音字母的结果有5种,则 P(一个元音)=满足三个全部为元音字母的结果有1种,则 P(三个元音)=满足只有两个元音字母的结果有4种,则 P(两个元音)= =新知探究(2)取出的3个小球上全是辅音字母的概率是多少?甲乙丙ACDEHIHIHIBCDEHIHIHI用树状图列举的结果看起来一目了然,当事件要经过多个(三个或三个以上)步骤完成时,用树状图法求事件的概率很有效.解:满足全是辅音字母的结果有2种,则
P(三个辅音)= = .新知探究经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件发生的概率:
(1)三辆车全部继续直行;
(2)两车向右,一车向左;
(3)至少两车向左.新知探究第一辆左右左右左直右第二辆第三辆直直左右直左右直左直右左直右左直右左直右左直右左直右左直右左直右共有27种行驶方向(2)P(两车向右,一车向左)= ;
(3) P(至少两车向左)= (1)P(全部直行)新知探究现有A,B,C三盘包子,已知A盘中有两个酸菜包和一个糖包,B盘中有一个酸菜包和一个糖包和一个韭菜包,C盘中有一个酸菜包和一个糖包以及一个馒头.老师就爱吃酸菜包.如果老师从每个盘中各选一个包子(馒头除外),那么老师选的包子全部是酸菜包的概率是多少?新知探究解:根据题意,画出树状图如下 由树状图得所有可能出现的结果有18种,它们出现的可能性相等.选的包子全部是酸菜包有2种,所以选的包子全部是酸菜包的概率是课堂小结树状图步骤用法是一种解决试验有多步(或涉及多个因素)的好方法.注意弄清试验涉及试验因素个数或试验步骤分几步;③利用概率公式进行计算.①关键要弄清楚每一步有几种结果;②在树状图下面对应写着所有可能
的结果;②在摸球试验一定要弄清“放回”还
是“不放回”.课堂小测1.a,b,c,d四本不同的书放入一个书包,至少放一本,最多放2本,共有 种不同的放法.2.三女一男四人同行,从中任意选出两人,其性别不同的概率为( )3.在一个不透明的布袋中装有2个白球和n个黄球,它们除颜色外,其余均相同,若从中随机摸出一个球,摸到黄球的概率为 ,则n= .
10C8A. B. C. D. 课堂小测4.在一个不透明的盒子里,装有三个分别写有数字6,-2,7的小球,它们的形状,大小,质地等完全相同.先从盒子里随机取出一个小球,记下数字后放回盒子里,摇匀后再随机取出一个小球,记下数字.请你用列表或画树形图的方法求下列事件发生的概率.
(1)两次取出的小球上的数字相同;
(2)两次取出的小球上的数字之和大于10.课堂小测(1)两次取出的小球上的数字相同的可能性只有3种,所以P(数字相同)=(2)两次取出的小球上的数字之和大于10的可能性只有4种,所以P(数字之和大于10)=解:根据题意,画出树状图如下
