沪科版九年级数学下册课件26.2.3概率的应用(22张)
文档属性
| 名称 | 沪科版九年级数学下册课件26.2.3概率的应用(22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-07 15:20:31 | ||
图片预览





文档简介
课件22张PPT。第二十六章
概率初步九年级数学沪科版·下册26.2.3概率的应用教学目标1.理解一元二次方程的概率.(难点)
2.根据一元二次方程的一般形式,确定各项系数.
3.理解并灵活运用一元二次方程概念解决有关问题.(重点)情景导入情境引入 我们在日常生活中经常会做一些游戏,游戏规则制定是否公平,对游戏者来说非常重要,其实这是一个游戏双方获胜概率大小的问题.思考:那么求概率的大
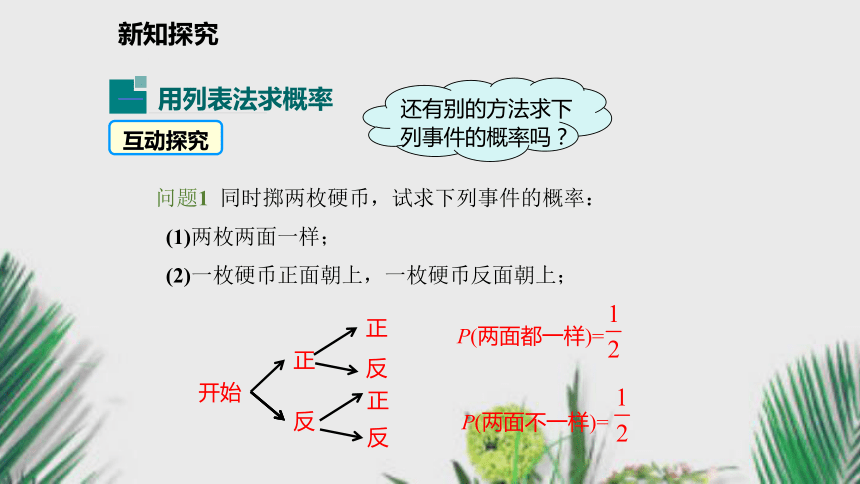
小有什么方法呢?新知探究 互动探究问题1 同时掷两枚硬币,试求下列事件的概率:
(1)两枚两面一样;
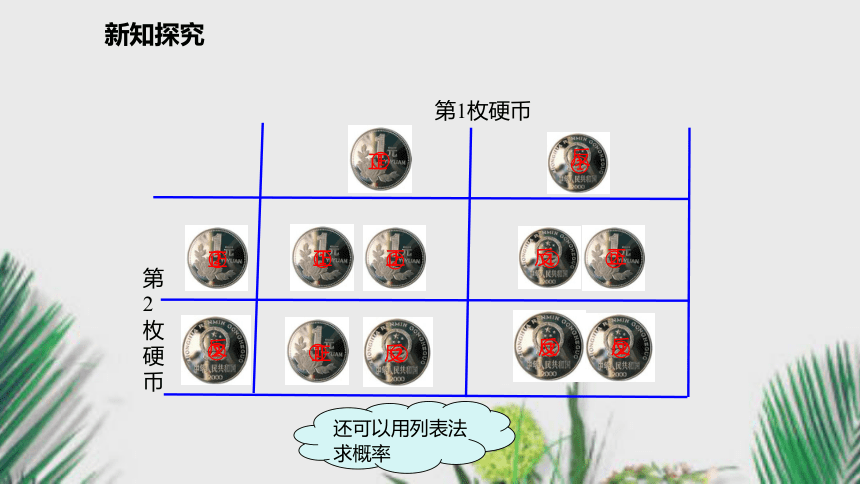
(2)一枚硬币正面朝上,一枚硬币反面朝上;新知探究第1枚硬币第
2
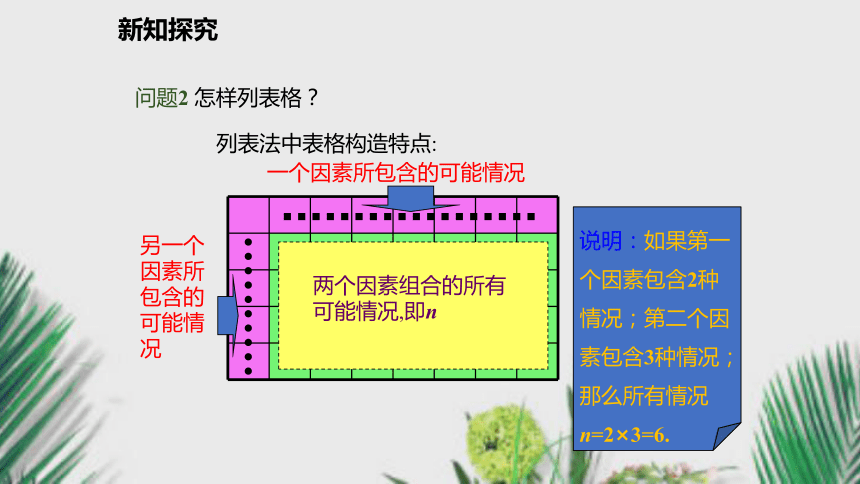
枚硬币反正正反正正反正正反反反新知探究问题2 怎样列表格? 一个因素所包含的可能情况另一个因素所包含的可能情况两个因素组合的所有可能情况,即n列表法中表格构造特点:新知探究例1 同时抛掷2枚均匀的骰子一次,骰子各面上的点数分别是1,2,···,6.试分别计算如下各随机事件的概率.
(1)抛出的点数之和等于8;
(2)抛出的点数之和等于12.分析:首先要弄清楚一共有多少个可能结果.第1枚骰子可能掷出1,2,···,6中的每一种情况,第2枚骰子也可能掷出1,2,···,6中的每一种情况.可以用“列表法”列出所有可能的结果如下:新知探究第2枚
骰子第1枚骰子结
果123456123456(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)(2,1)(3,1)(4,1)(5,1)(6,1)(2,2)(2,3)(2,4)(2,5)(2,6)(3,2)(3,3)(3,4)(3,5)(3,6)(4,2)(5,2)(6,2)(4,3)(5,3)(6,3)(4,4)(5,4)(6,4)(4,5)(5,5)(6,5)(4,6)(5,6)(6,6)新知探究解:从上表可以看出,同时抛掷两枚骰子一次,所有可能出现的结果有36种.由于骰子是均匀的,所以每个结果出现的可能性相等.新知探究当一次试验要涉及两个因素(例如掷两个骰子)并且可能出现的结果数目较多时,为不重不漏地列出所有可能结果,通常采用列表法.新知探究典例精析例2 “石头,剪刀,布”是民间 广为流传的一种游戏,游戏的两人每次做“石头”“剪刀”“布”三种手势中的一种,并约定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,同种手势不分胜负须继续比赛.现有甲、乙两人做这种游戏.
(1)一次游戏中甲获胜、乙获胜的概率各是多少?
(2)这种游戏对于两个人来说公平吗?新知探究解:若分别用A,B表示甲、乙两人,用1,2,3表示石头、剪刀、布,则A1表示甲出石头、B2表示乙出剪刀,依次类推.于是游戏的所有结果用“树状图”来表示:开始甲A1A2A3乙 B1 B2 B3 B1 B2 B3 B1 B2 B3新知探究所有结果是9种,且出现的可能性相等.因此,一次游戏时:新知探究例3 某人的密码箱由三个数字组成,每个数字都是从0~9中任选的.如果他忘记了自己设定的密码,求在一次随机试验中他能打开箱子的概率.解:设在一次随机试验中他能打开箱子的事件为A,根据题意,在一次随机试验中选择的号码应是000~999中的任意一个3位数,所有可能出现的结果共有1000种,且出现每一种结果的可能性相等.要能打开箱子,即选择的号码与密码相同的结果只有一种,所以新知探究例4 甲、乙两人要去风景区游玩,仅知道每天开往风景区有3辆汽车,并且舒适程度分别为上等、中等、下等3种,但不知道怎样区分这些车,也不知道它们会以怎样的顺序开来.于是他们分别采用了不同的乘车办法:甲乘第1辆开来的车.乙不乘第1辆车,并且仔细观察第2辆车的情况,如比第1辆车好,就乘第2辆车;如不比第1辆车好,就乘第3辆车.试问甲、乙两人的乘车办法,哪一种更有利于乘上舒适度较好的车?新知探究解:容易知道3辆汽车开来的先后顺序有如下6种可能情况:(上中下),(上下中),(中上下),(中下上),(下上中),(下中上).假定6种顺序出现的可能性相等, 在各种可能顺序之下,甲、乙两人分别会乘坐的汽车列表如下: 上下上中中上中上下上下中答:乙的乘车办法更有利于乘上舒适度较好的车.新知探究1.当一次试验只涉及一个因素时,可直接利用概率公式计算;
2.当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重复、不遗漏地列出所有可能的结果,通常用列表法;
3.当一次试验要涉及两个或两个以上因素时,为了不重复、不遗漏地列出所有可能的结果,通常采用树状图法;课堂小结列举法基本步骤前提条件常用
方法直接列举法列表法画树状图法列举(列表或画树状图);
确定m,n值,代入概率公式计算.确保试验中每种结果出现的可能性大小相等.涉及一个因素时直接利用公式计算涉及两个或两个以上的因素涉及两个因素且可能出现的结果数目较多课堂小测 1.小明与小红玩一次“石头、剪刀、布”游戏,则小明赢的概率是( )
2.某次考试中,每道单项选择题一般有4个选项,某同学有两道题不会做,于是他以“抓阄”的方式选定其中一个答案,则该同学的这两道题全对的概率是( )
CDA. B. C. D. A. B. C. D. 课堂小测3.如果有两组牌,它们的牌面数字分别是1,2,3,那么从每组牌中各摸出一张牌.(1)摸出两张牌的数字之和为4的概率是多少?(2)摸出两张牌的数字相等的概率是多少?课堂小测321321 解:(1)P(数字之和为4)= . 课堂小测4.小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清随便穿了两只就去上学,问小明正好穿的是相同的一双袜子的概率是多少?解:设两双袜子分别为A1,A2,B1,B2,则
2.根据一元二次方程的一般形式,确定各项系数.
3.理解并灵活运用一元二次方程概念解决有关问题.(重点)情景导入情境引入 我们在日常生活中经常会做一些游戏,游戏规则制定是否公平,对游戏者来说非常重要,其实这是一个游戏双方获胜概率大小的问题.思考:那么求概率的大
小有什么方法呢?新知探究 互动探究问题1 同时掷两枚硬币,试求下列事件的概率:
(1)两枚两面一样;
(2)一枚硬币正面朝上,一枚硬币反面朝上;新知探究第1枚硬币第
2
枚硬币反正正反正正反正正反反反新知探究问题2 怎样列表格? 一个因素所包含的可能情况另一个因素所包含的可能情况两个因素组合的所有可能情况,即n列表法中表格构造特点:新知探究例1 同时抛掷2枚均匀的骰子一次,骰子各面上的点数分别是1,2,···,6.试分别计算如下各随机事件的概率.
(1)抛出的点数之和等于8;
(2)抛出的点数之和等于12.分析:首先要弄清楚一共有多少个可能结果.第1枚骰子可能掷出1,2,···,6中的每一种情况,第2枚骰子也可能掷出1,2,···,6中的每一种情况.可以用“列表法”列出所有可能的结果如下:新知探究第2枚
骰子第1枚骰子结
果123456123456(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)(2,1)(3,1)(4,1)(5,1)(6,1)(2,2)(2,3)(2,4)(2,5)(2,6)(3,2)(3,3)(3,4)(3,5)(3,6)(4,2)(5,2)(6,2)(4,3)(5,3)(6,3)(4,4)(5,4)(6,4)(4,5)(5,5)(6,5)(4,6)(5,6)(6,6)新知探究解:从上表可以看出,同时抛掷两枚骰子一次,所有可能出现的结果有36种.由于骰子是均匀的,所以每个结果出现的可能性相等.新知探究当一次试验要涉及两个因素(例如掷两个骰子)并且可能出现的结果数目较多时,为不重不漏地列出所有可能结果,通常采用列表法.新知探究典例精析例2 “石头,剪刀,布”是民间 广为流传的一种游戏,游戏的两人每次做“石头”“剪刀”“布”三种手势中的一种,并约定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,同种手势不分胜负须继续比赛.现有甲、乙两人做这种游戏.
(1)一次游戏中甲获胜、乙获胜的概率各是多少?
(2)这种游戏对于两个人来说公平吗?新知探究解:若分别用A,B表示甲、乙两人,用1,2,3表示石头、剪刀、布,则A1表示甲出石头、B2表示乙出剪刀,依次类推.于是游戏的所有结果用“树状图”来表示:开始甲A1A2A3乙 B1 B2 B3 B1 B2 B3 B1 B2 B3新知探究所有结果是9种,且出现的可能性相等.因此,一次游戏时:新知探究例3 某人的密码箱由三个数字组成,每个数字都是从0~9中任选的.如果他忘记了自己设定的密码,求在一次随机试验中他能打开箱子的概率.解:设在一次随机试验中他能打开箱子的事件为A,根据题意,在一次随机试验中选择的号码应是000~999中的任意一个3位数,所有可能出现的结果共有1000种,且出现每一种结果的可能性相等.要能打开箱子,即选择的号码与密码相同的结果只有一种,所以新知探究例4 甲、乙两人要去风景区游玩,仅知道每天开往风景区有3辆汽车,并且舒适程度分别为上等、中等、下等3种,但不知道怎样区分这些车,也不知道它们会以怎样的顺序开来.于是他们分别采用了不同的乘车办法:甲乘第1辆开来的车.乙不乘第1辆车,并且仔细观察第2辆车的情况,如比第1辆车好,就乘第2辆车;如不比第1辆车好,就乘第3辆车.试问甲、乙两人的乘车办法,哪一种更有利于乘上舒适度较好的车?新知探究解:容易知道3辆汽车开来的先后顺序有如下6种可能情况:(上中下),(上下中),(中上下),(中下上),(下上中),(下中上).假定6种顺序出现的可能性相等, 在各种可能顺序之下,甲、乙两人分别会乘坐的汽车列表如下: 上下上中中上中上下上下中答:乙的乘车办法更有利于乘上舒适度较好的车.新知探究1.当一次试验只涉及一个因素时,可直接利用概率公式计算;
2.当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重复、不遗漏地列出所有可能的结果,通常用列表法;
3.当一次试验要涉及两个或两个以上因素时,为了不重复、不遗漏地列出所有可能的结果,通常采用树状图法;课堂小结列举法基本步骤前提条件常用
方法直接列举法列表法画树状图法列举(列表或画树状图);
确定m,n值,代入概率公式计算.确保试验中每种结果出现的可能性大小相等.涉及一个因素时直接利用公式计算涉及两个或两个以上的因素涉及两个因素且可能出现的结果数目较多课堂小测 1.小明与小红玩一次“石头、剪刀、布”游戏,则小明赢的概率是( )
2.某次考试中,每道单项选择题一般有4个选项,某同学有两道题不会做,于是他以“抓阄”的方式选定其中一个答案,则该同学的这两道题全对的概率是( )
CDA. B. C. D. A. B. C. D. 课堂小测3.如果有两组牌,它们的牌面数字分别是1,2,3,那么从每组牌中各摸出一张牌.(1)摸出两张牌的数字之和为4的概率是多少?(2)摸出两张牌的数字相等的概率是多少?课堂小测321321 解:(1)P(数字之和为4)= . 课堂小测4.小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清随便穿了两只就去上学,问小明正好穿的是相同的一双袜子的概率是多少?解:设两双袜子分别为A1,A2,B1,B2,则
