6.2 立方根课件
图片预览





文档简介
(共24张PPT)
人教版 七年级数学下
6.2立方根
学习目标
1.了解立方根的概念,会用立方运算求一个数的立
方根;(重点)
2.了解立方根的性质,并学会用计算器计算一个数
的立方根或立方根的近似值.(重点、难点)
回顾旧知
1.什么叫做平方根?
如果一个数的平方等于a,那么这个数叫做a的平方根(也叫二次方根). 即:x2=a,那么x叫做a的平方根。
a的平方根记作:_______
2、对于正数、0、负数,它们的平方根分别具有什么性质呢?
①、正数有两个平方根,它们互为相反数;
②、0的平方根是0;
③、负数没有平方根.
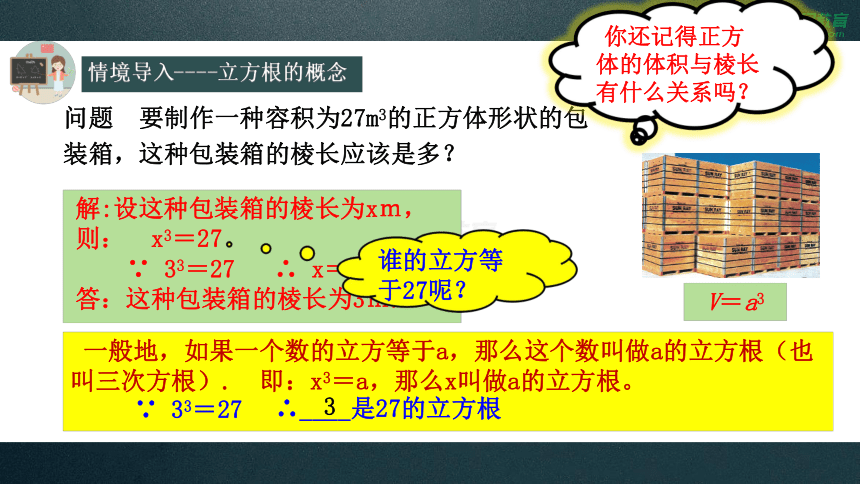
情境导入----立方根的概念
问题 要制作一种容积为27m3的正方体形状的包装箱,这种包装箱的棱长应该是多?
解:设这种包装箱的棱长为xm,
则: x3=27
∵ 33=27 ∴ x=3
答:这种包装箱的棱长为3m.
你还记得正方体的体积与棱长有什么关系吗?
V=a3
谁的立方等于27呢?
一般地,如果一个数的立方等于a,那么这个数叫做a的立方根(也叫三次方根). 即:x3=a,那么x叫做a的立方根。
∵ 33=27
∴____是27的立方根
3
小试牛刀
求下列各数的立方根:
解:(1)∵(-0.1)3=-0.001 ∴ -0.001的立方根是-0.1
(2)∵( )3= ∴ 的立方根是
(3)∵(10)3= ∴ 的立方根是10
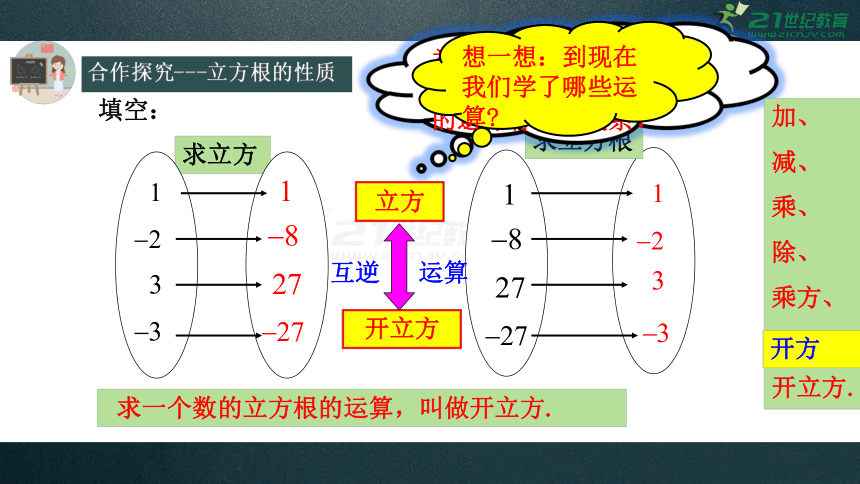
合作探究---立方根的性质
填空:
求立方
求立方根
类比平方与开平方的互逆关系, 左右两图中的运算有什么关系?
立方
开立方
互逆 运算
求一个数的立方根的运算,叫做开立方.
想一想:到现在我们学了哪些运算?
加、
减、
乘、
除、
乘方、
开平方、
开立方.
开方
根据立方根的意义填空.你能发现正数、0和负数的立方根各有什么特点吗?
∵( )3 =8, ∴8的立方根是( );
∵( )3 =0.064 , ∴ 0.064的立方根是( );
∵( )3 = 0, ∴ 0的立方根是( );
∵( )3 =-8 , ∴ -8的立方根是( );
∵( )3 = , ∴ 的立方根是( ).
2
2
0.4
0.4
0
0
-2
-2
合作探究---立方根的性质
类比平方根的性质,你能说说立方根的性质吗?
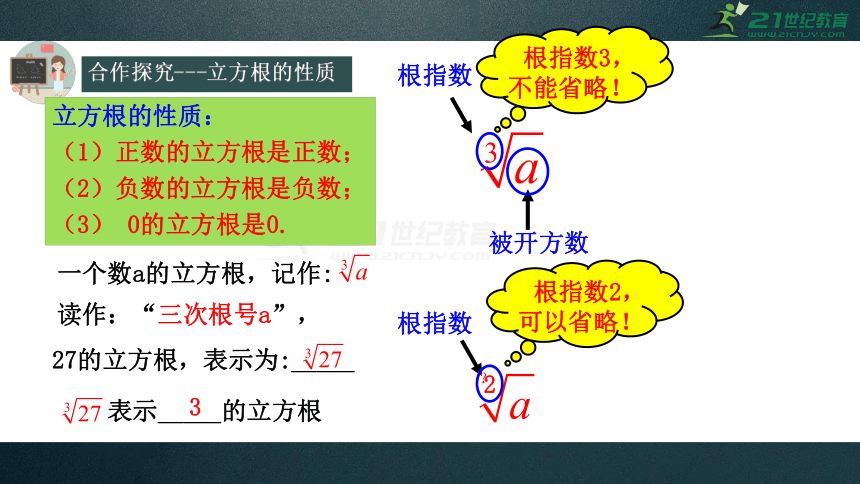
立方根的性质:
(1)正数的立方根是正数;
(2)负数的立方根是负数;
(3) 0的立方根是0.
一个数a的立方根,记作:
读作:“三次根号a”,
被开方数
根指数
根指数3,不能省略!
27的立方根,表示为:_____
表示_____的立方根
3
根指数
?
2
根指数2,可以省略!
合作探究---立方根的性质
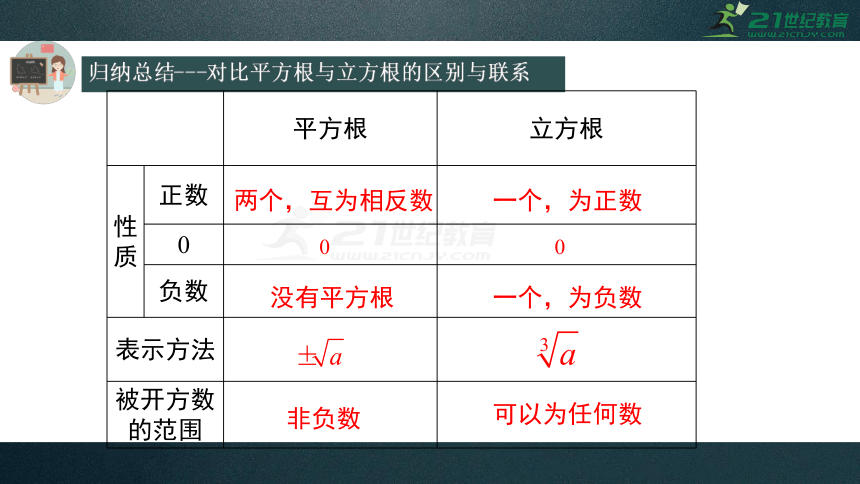
归纳总结---对比平方根与立方根的区别与联系
平方根 立方根
性
质 正数
0
负数
表示方法
被开方数的范围
两个,互为相反数
一个,为正数
0
0
没有平方根
一个,为负数
可以为任何数
非负数
小试牛刀
判断下列说法是否正确, 并说明理由.
(2) ±4是64的立方根 ( )
(3) 是 立方根( )
(4) 的立方根是-4( )
(5) 0的平方根和立方根都是0 ( )
(1)
2是8的立方根
( )
×
√
√
×
√
思考1:立方根是它本身的数有那些?
思考2:算术平方根是它本身的数有那些?
0,±1
0,1
合作探究---立方根的性质
一般地, .
填空,你能发现其中的规律吗?
因为 = ,
所以
因为
所以
-2
=
=
-2
-3
-3
小试牛刀
例:求下列各式的值 :
解:
还有别的算法吗?
正确使用计算器求立方根
解:(1) 依次按键 、8 、 ,
显示:2.
∴ .
(2) 依次按键 、1845、 ,
显示:12.264 940 81.
∴ .
被开方数
由于一个数的立方根可能是无限不循环小数,所以我们可以利用计算器求一个数的立方根或它的近似值用计算器求下列各式的值:.
(1). (2).
1、利用计算器计算,并将计算结果填在表中,你发现了什么规律?
规律:被开方数的小数点向右(或向左)移动3位,其算术平方根的小数点向右(或向左)移动1位.
… …
… …
0.06
0.6
6
60
正确使用计算器求立方根
2、 你能用计算器计算 (精确到0.001)吗?并利用刚才的得到规律说出 , , 的近似值.
想一想: 你能否根据 的值说出 是多少?
解:
答:不能
正确使用计算器求立方根
小试牛刀
1. 你能比较3,4, 的<大小吗?
解:∵33=27,
∴
∵ 43=64 ,
∴
∵
∴
被开方数越大,对应的立方根也越大.
<
<
<
<
小试牛刀
2.立方根概念的起源与几何中的正方体有关,如果一个正方体的体积为V,那么这个正方体的棱长为多少?
解:
3. 求下列各式中的 x:
(1) x3-3= ; (2) (x-1)3=64.
解: (1) x3-3=
x3=
(2) (x-1)3=64
∵43=64
∴x-1=4
x=5
∵( )3= ∴x=
课堂小结
畅谈收获:今天我们学习了哪些知识?
1.什么是立方根?怎么表示立方根?
2.如何求一个数的立方根?
3.立方根有什么性质?与平方根有什么区别与联系?
4.如何用计算器求一个数的立方根?
综合演练
1. 的平方根是( )
A.2 B.±2 C. D. ±
D
2. 下列各数中,立方根一定是负数的 是( )
A.-a B. C. D.
C
知识点拨:本题需要认真审题,分两步计算。
知识点拨:立方根是负数的被开方数一定是负数,从而选出是C。
综合演练
3. 估计68的立方根分布在___与 __之间(填写相邻的两个整数)。
4
知识点拨:我们知道4的立方等于64,5的立方等于125,68位于65与125之间,所以68的立方根在4 ~ 5之间。
4. ,则m-n的值为_______.
0或10
知识点拨:有题意m=±5,n=-5,所有求m-n的值时需要分两种情况讨论。
5
综合演练
6.比较下列各组数的大小.
(1) 与2.5; (2) 与 .
解:因为 = 9
2.53 = 15.625
所以 < 15.625
所以 < 2.5
因为 = 3
所以3 <
所以 <
综合演练
6.若 =2, =4,求 的值.
解:∵ =2, =4.
∴x = 23,y2 = 16,
∴x = 8,y = ±4.
∴x + 2y = 8 + 2×4 = 16 或 x + 2y = 8 – 2×4 = 0.
∴ = = 4 或 = = 0.
课后作业
课本教材第52页:3、5题
https://www.21cnjy.com/help/help_extract.php
人教版 七年级数学下
6.2立方根
学习目标
1.了解立方根的概念,会用立方运算求一个数的立
方根;(重点)
2.了解立方根的性质,并学会用计算器计算一个数
的立方根或立方根的近似值.(重点、难点)
回顾旧知
1.什么叫做平方根?
如果一个数的平方等于a,那么这个数叫做a的平方根(也叫二次方根). 即:x2=a,那么x叫做a的平方根。
a的平方根记作:_______
2、对于正数、0、负数,它们的平方根分别具有什么性质呢?
①、正数有两个平方根,它们互为相反数;
②、0的平方根是0;
③、负数没有平方根.
情境导入----立方根的概念
问题 要制作一种容积为27m3的正方体形状的包装箱,这种包装箱的棱长应该是多?
解:设这种包装箱的棱长为xm,
则: x3=27
∵ 33=27 ∴ x=3
答:这种包装箱的棱长为3m.
你还记得正方体的体积与棱长有什么关系吗?
V=a3
谁的立方等于27呢?
一般地,如果一个数的立方等于a,那么这个数叫做a的立方根(也叫三次方根). 即:x3=a,那么x叫做a的立方根。
∵ 33=27
∴____是27的立方根
3
小试牛刀
求下列各数的立方根:
解:(1)∵(-0.1)3=-0.001 ∴ -0.001的立方根是-0.1
(2)∵( )3= ∴ 的立方根是
(3)∵(10)3= ∴ 的立方根是10
合作探究---立方根的性质
填空:
求立方
求立方根
类比平方与开平方的互逆关系, 左右两图中的运算有什么关系?
立方
开立方
互逆 运算
求一个数的立方根的运算,叫做开立方.
想一想:到现在我们学了哪些运算?
加、
减、
乘、
除、
乘方、
开平方、
开立方.
开方
根据立方根的意义填空.你能发现正数、0和负数的立方根各有什么特点吗?
∵( )3 =8, ∴8的立方根是( );
∵( )3 =0.064 , ∴ 0.064的立方根是( );
∵( )3 = 0, ∴ 0的立方根是( );
∵( )3 =-8 , ∴ -8的立方根是( );
∵( )3 = , ∴ 的立方根是( ).
2
2
0.4
0.4
0
0
-2
-2
合作探究---立方根的性质
类比平方根的性质,你能说说立方根的性质吗?
立方根的性质:
(1)正数的立方根是正数;
(2)负数的立方根是负数;
(3) 0的立方根是0.
一个数a的立方根,记作:
读作:“三次根号a”,
被开方数
根指数
根指数3,不能省略!
27的立方根,表示为:_____
表示_____的立方根
3
根指数
?
2
根指数2,可以省略!
合作探究---立方根的性质
归纳总结---对比平方根与立方根的区别与联系
平方根 立方根
性
质 正数
0
负数
表示方法
被开方数的范围
两个,互为相反数
一个,为正数
0
0
没有平方根
一个,为负数
可以为任何数
非负数
小试牛刀
判断下列说法是否正确, 并说明理由.
(2) ±4是64的立方根 ( )
(3) 是 立方根( )
(4) 的立方根是-4( )
(5) 0的平方根和立方根都是0 ( )
(1)
2是8的立方根
( )
×
√
√
×
√
思考1:立方根是它本身的数有那些?
思考2:算术平方根是它本身的数有那些?
0,±1
0,1
合作探究---立方根的性质
一般地, .
填空,你能发现其中的规律吗?
因为 = ,
所以
因为
所以
-2
=
=
-2
-3
-3
小试牛刀
例:求下列各式的值 :
解:
还有别的算法吗?
正确使用计算器求立方根
解:(1) 依次按键 、8 、 ,
显示:2.
∴ .
(2) 依次按键 、1845、 ,
显示:12.264 940 81.
∴ .
被开方数
由于一个数的立方根可能是无限不循环小数,所以我们可以利用计算器求一个数的立方根或它的近似值用计算器求下列各式的值:.
(1). (2).
1、利用计算器计算,并将计算结果填在表中,你发现了什么规律?
规律:被开方数的小数点向右(或向左)移动3位,其算术平方根的小数点向右(或向左)移动1位.
… …
… …
0.06
0.6
6
60
正确使用计算器求立方根
2、 你能用计算器计算 (精确到0.001)吗?并利用刚才的得到规律说出 , , 的近似值.
想一想: 你能否根据 的值说出 是多少?
解:
答:不能
正确使用计算器求立方根
小试牛刀
1. 你能比较3,4, 的<大小吗?
解:∵33=27,
∴
∵ 43=64 ,
∴
∵
∴
被开方数越大,对应的立方根也越大.
<
<
<
<
小试牛刀
2.立方根概念的起源与几何中的正方体有关,如果一个正方体的体积为V,那么这个正方体的棱长为多少?
解:
3. 求下列各式中的 x:
(1) x3-3= ; (2) (x-1)3=64.
解: (1) x3-3=
x3=
(2) (x-1)3=64
∵43=64
∴x-1=4
x=5
∵( )3= ∴x=
课堂小结
畅谈收获:今天我们学习了哪些知识?
1.什么是立方根?怎么表示立方根?
2.如何求一个数的立方根?
3.立方根有什么性质?与平方根有什么区别与联系?
4.如何用计算器求一个数的立方根?
综合演练
1. 的平方根是( )
A.2 B.±2 C. D. ±
D
2. 下列各数中,立方根一定是负数的 是( )
A.-a B. C. D.
C
知识点拨:本题需要认真审题,分两步计算。
知识点拨:立方根是负数的被开方数一定是负数,从而选出是C。
综合演练
3. 估计68的立方根分布在___与 __之间(填写相邻的两个整数)。
4
知识点拨:我们知道4的立方等于64,5的立方等于125,68位于65与125之间,所以68的立方根在4 ~ 5之间。
4. ,则m-n的值为_______.
0或10
知识点拨:有题意m=±5,n=-5,所有求m-n的值时需要分两种情况讨论。
5
综合演练
6.比较下列各组数的大小.
(1) 与2.5; (2) 与 .
解:因为 = 9
2.53 = 15.625
所以 < 15.625
所以 < 2.5
因为 = 3
所以3 <
所以 <
综合演练
6.若 =2, =4,求 的值.
解:∵ =2, =4.
∴x = 23,y2 = 16,
∴x = 8,y = ±4.
∴x + 2y = 8 + 2×4 = 16 或 x + 2y = 8 – 2×4 = 0.
∴ = = 4 或 = = 0.
课后作业
课本教材第52页:3、5题
https://www.21cnjy.com/help/help_extract.php
