2.1.2向量的几何表示(共16张PPT)
文档属性
| 名称 | 2.1.2向量的几何表示(共16张PPT) | 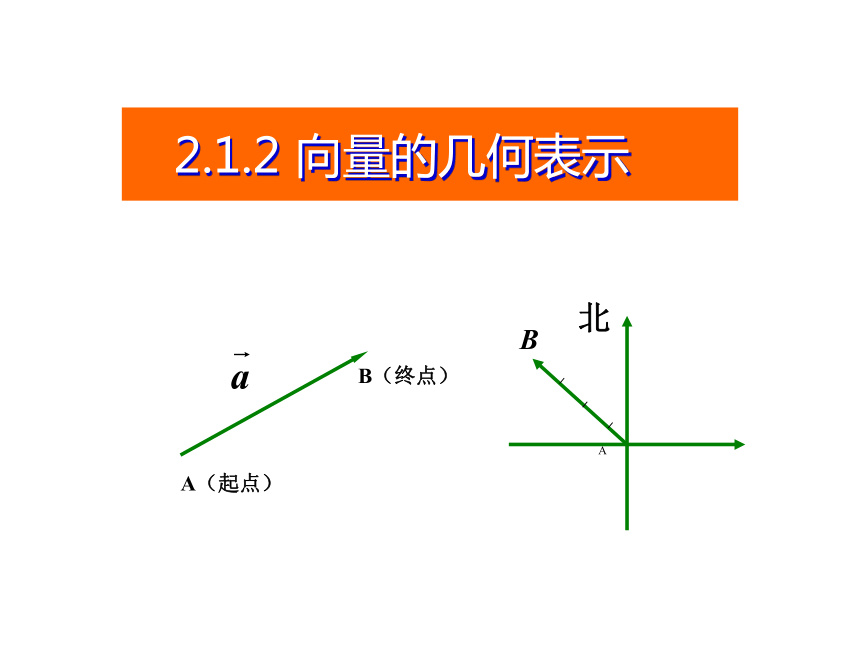 | |
| 格式 | zip | ||
| 文件大小 | 364.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 11:36:43 | ||
图片预览






文档简介
(共16张PPT)
2.1.2 向量的几何表示
既有大小,又有方向的量叫做向量。
向量的概念:
数量只有大小,是一个代数量,可以进行代数运算、比较大小;
向量有方向,大小,因为方向性所以不能比较大小。
数量与向量的区别:
由于实数与数轴上的点一一对应,所以数量常常用数轴上的一个点表示,如3,2,-1,…而且不同的点表示不同的数量。
对于向量,我们常用带箭头的线段来表示,线段按一定比例(标度)画出,它的长度表示向量的大小,箭头表示向量的方向。
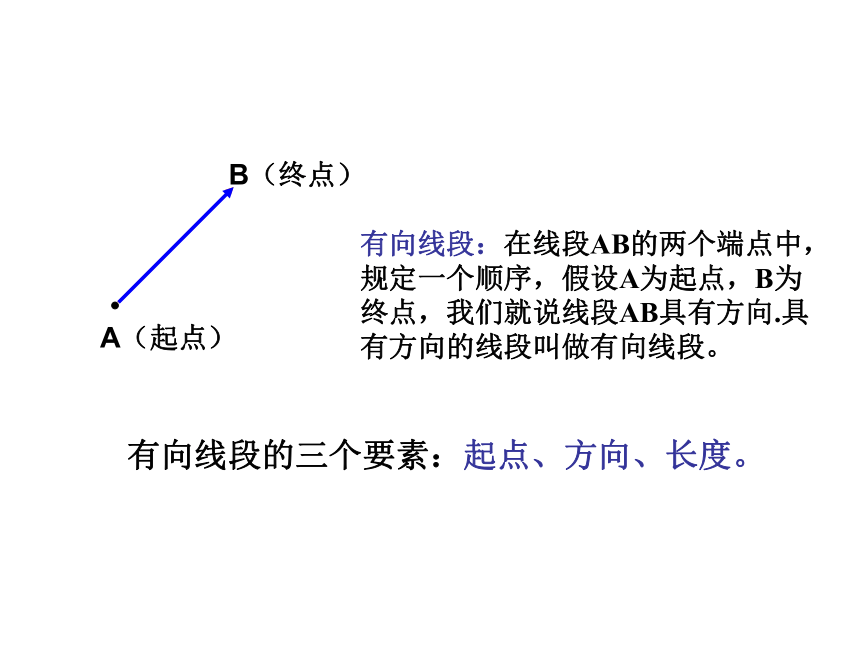
有向线段:在线段AB的两个端点中,规定一个顺序,假设A为起点,B为终点,我们就说线段AB具有方向.具有方向的线段叫做有向线段。
有向线段的三个要素:起点、方向、长度。
A(起点)
B(终点)
1、向量的几何表示:用有向线段表示。
思考: “向量就是有向线段,有向线段就是向量.”的说法对吗?
两个特殊的向量:
单位向量——长度(模)为1个单位长度的
向量叫做单位向量。
例1:温度有零上零下之分,“温度”是否向量?
答:不是同一向量。
答:不是,因为零上零下也只是大小之分。
方向相同或相反的非零向量叫做平行向量。
例3:有几个单位向量?单位向量的大小是否相等?单位向量是否都相等?是否都平行?
答:有无数个单位向量,单位向量大小相等,单位向量不一定相等,不是都平行。
5.单位向量
长度等于1个单位的向量,叫做单位向量。
问答:
(1)平行向量是否一定方向相同?
(2)不相等的向量是否一定不平行?
(3)与零向量相等的向量必定是什么向量?
不一定
不一定
零向量
(4)与任意向量都平行的向量是什么向量?
(5)若两个向量在同一直线上,则这两个向量
一定是什么向量?
(6)两个非零向量相等的时候当且仅当什么?
平行向量
零向量
长度相等且方向相同
1.温度含零上和零下温度,所以温度是向量( )
2.向量的模是一个正实数( )
注:向量不能比较大小
判断:
2.1.2 向量的几何表示
既有大小,又有方向的量叫做向量。
向量的概念:
数量只有大小,是一个代数量,可以进行代数运算、比较大小;
向量有方向,大小,因为方向性所以不能比较大小。
数量与向量的区别:
由于实数与数轴上的点一一对应,所以数量常常用数轴上的一个点表示,如3,2,-1,…而且不同的点表示不同的数量。
对于向量,我们常用带箭头的线段来表示,线段按一定比例(标度)画出,它的长度表示向量的大小,箭头表示向量的方向。
有向线段:在线段AB的两个端点中,规定一个顺序,假设A为起点,B为终点,我们就说线段AB具有方向.具有方向的线段叫做有向线段。
有向线段的三个要素:起点、方向、长度。
A(起点)
B(终点)
1、向量的几何表示:用有向线段表示。
思考: “向量就是有向线段,有向线段就是向量.”的说法对吗?
两个特殊的向量:
单位向量——长度(模)为1个单位长度的
向量叫做单位向量。
例1:温度有零上零下之分,“温度”是否向量?
答:不是同一向量。
答:不是,因为零上零下也只是大小之分。
方向相同或相反的非零向量叫做平行向量。
例3:有几个单位向量?单位向量的大小是否相等?单位向量是否都相等?是否都平行?
答:有无数个单位向量,单位向量大小相等,单位向量不一定相等,不是都平行。
5.单位向量
长度等于1个单位的向量,叫做单位向量。
问答:
(1)平行向量是否一定方向相同?
(2)不相等的向量是否一定不平行?
(3)与零向量相等的向量必定是什么向量?
不一定
不一定
零向量
(4)与任意向量都平行的向量是什么向量?
(5)若两个向量在同一直线上,则这两个向量
一定是什么向量?
(6)两个非零向量相等的时候当且仅当什么?
平行向量
零向量
长度相等且方向相同
1.温度含零上和零下温度,所以温度是向量( )
2.向量的模是一个正实数( )
注:向量不能比较大小
判断:
