2.4.1 平面向量数量积的物理背景及其含义(共39张PPT)
文档属性
| 名称 | 2.4.1 平面向量数量积的物理背景及其含义(共39张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 00:00:00 | ||
图片预览





文档简介
(共39张PPT)
2.4.1 平面向量数量积的物理背景及其含义
回忆向量夹角概念
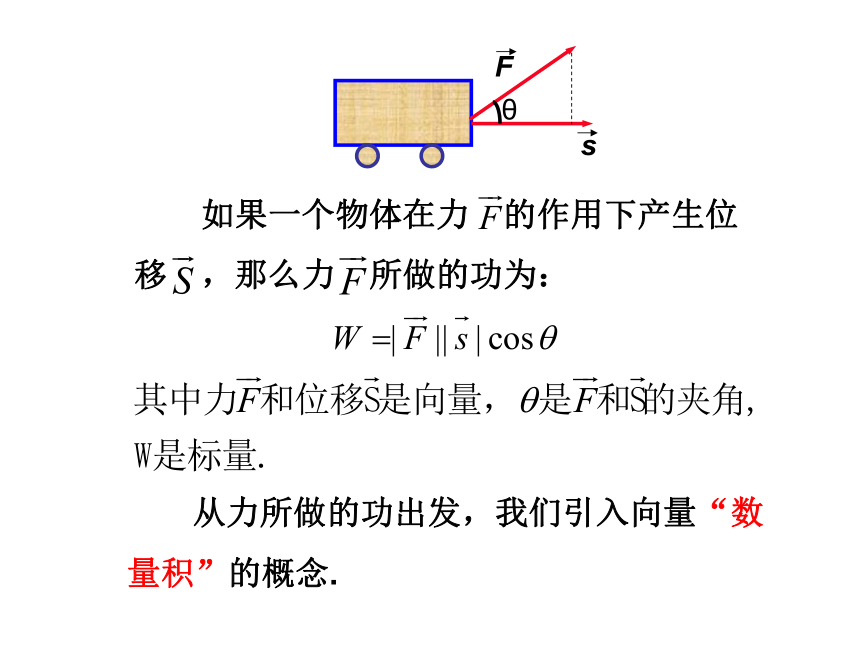
问题(1)功的数学本质是什么?
(2)尝试练习.
一物体质量是10千克,分别做以下运动,求重力做功 的大小。
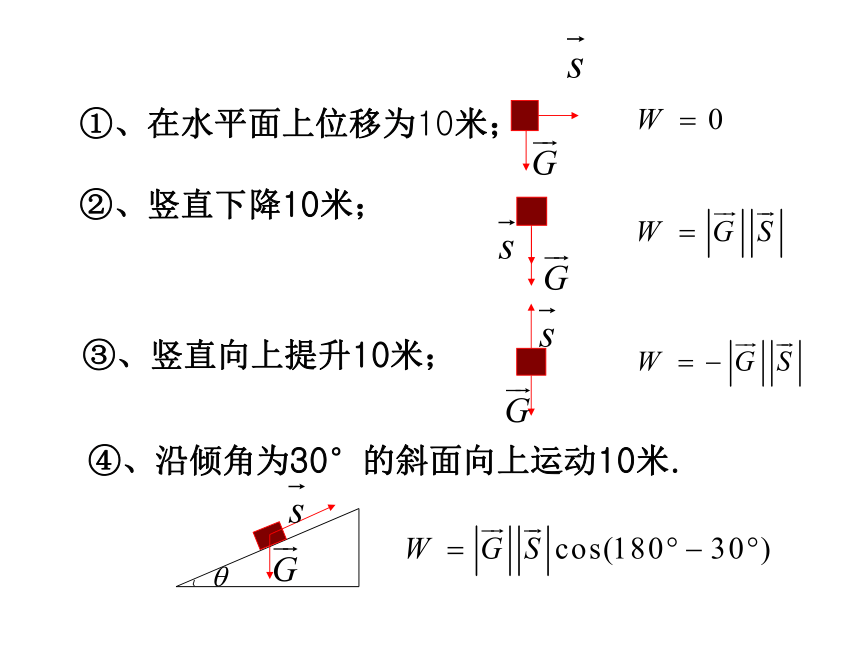
①、在水平面上位移为10米;
②、竖直下降10米;
③、竖直向上提升10米;
④、沿倾角为30度的斜面向上运动10米.
研究数量积的物理意义
④、沿倾角为30°的斜面向上运动10米.
②、竖直下降10米;
③、竖直向上提升10米;
①、在水平面上位移为10米;
从力所做的功出发,我们引入向量“数量积”的概念.
向量的数量积概念:
已知非零向量 与 ,我们把数量
叫作 与 的数量积(或内积),记作 ,即规定:
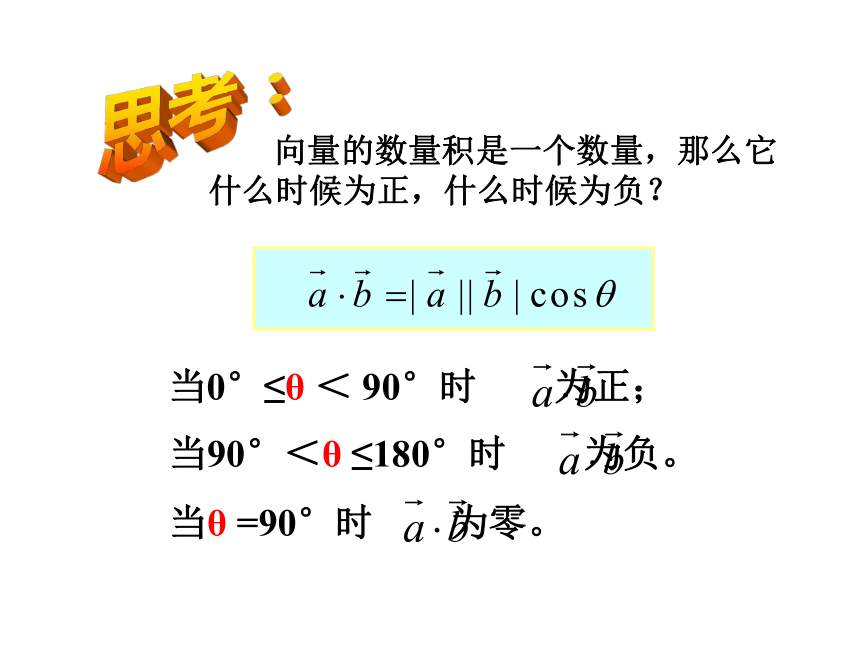
向量的数量积是一个数量,那么它什么时候为正,什么时候为负?
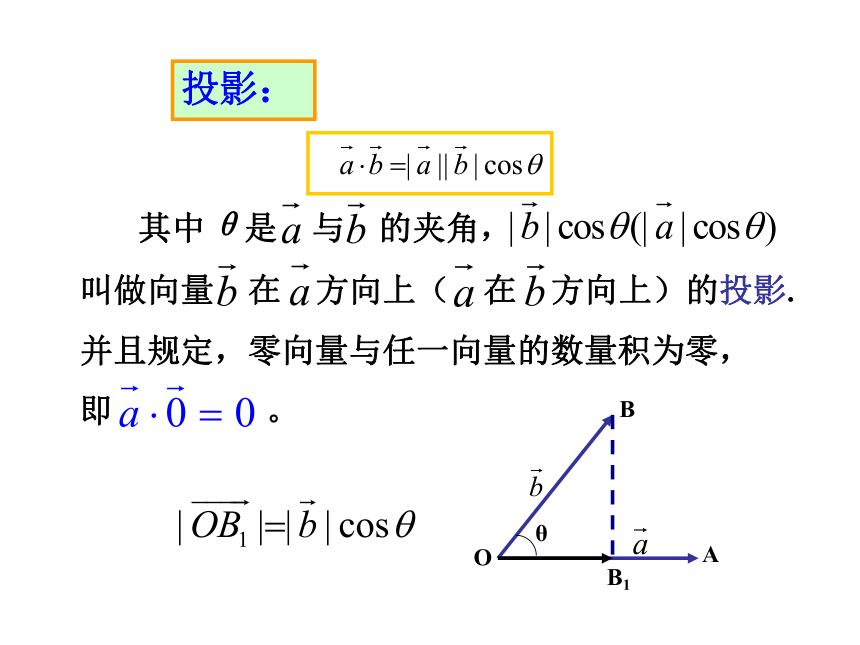
投影:
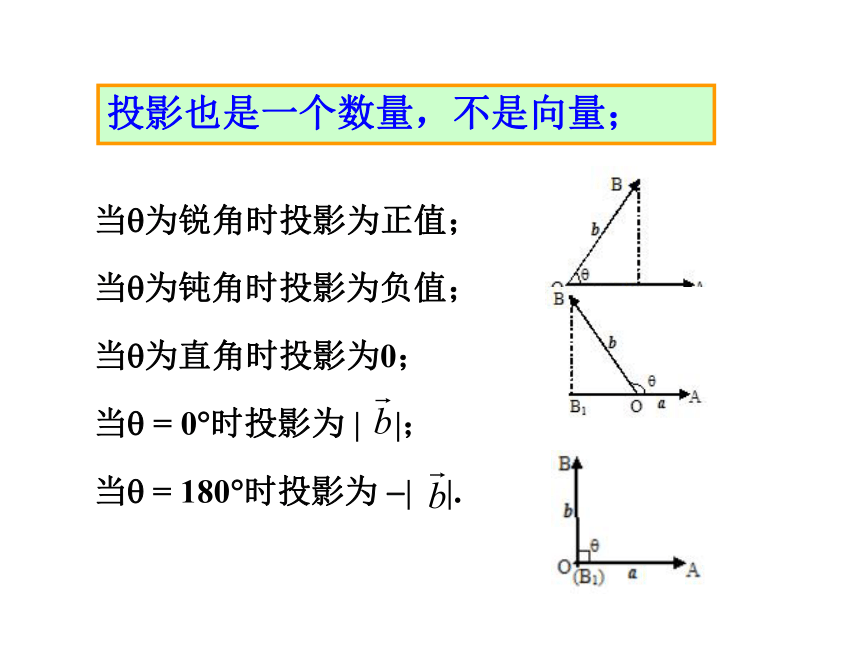
投影也是一个数量,不是向量;
当?为锐角时投影为正值;
当?为钝角时投影为负值;
当?为直角时投影为0;
由向量数量积的定义,试完成下面问题:
0
≤
证明向量
垂直的依据
解:
数量积的几何意义:
数量积的运算规律:
数量积的运算规律:
不成立
探究:两个向量的数量积与数的乘法有很大区别
(1)两个向量的数量积是一个实数,不是向量,符号由cos?的符号所决定.
解:
解:
(1)
(2)
解:
即
1、数量积的概念
2、数量积几何意义
3、重要性质
4、运算律
1、判断下列各题正确与否:
(1)若 ,则对任一向量 ,有 ( )
(2)若 ,则对任一非零向量 ,有 ( )
(3)若 , ,则 . ( )
(4)若 ,则 至少有一个为零. ( )
√
×
×
×
×
×
×
√
18或-2
D
5、若向量 与 的夹角为60°,
则 向量的模( )
A.2 B.4 C.6 D.12
C
1、
2、
时,△ABC为钝角三角形;
时,△ABC为直角三角形;
3.
投影分别为 投影如图.
2.4.1 平面向量数量积的物理背景及其含义
回忆向量夹角概念
问题(1)功的数学本质是什么?
(2)尝试练习.
一物体质量是10千克,分别做以下运动,求重力做功 的大小。
①、在水平面上位移为10米;
②、竖直下降10米;
③、竖直向上提升10米;
④、沿倾角为30度的斜面向上运动10米.
研究数量积的物理意义
④、沿倾角为30°的斜面向上运动10米.
②、竖直下降10米;
③、竖直向上提升10米;
①、在水平面上位移为10米;
从力所做的功出发,我们引入向量“数量积”的概念.
向量的数量积概念:
已知非零向量 与 ,我们把数量
叫作 与 的数量积(或内积),记作 ,即规定:
向量的数量积是一个数量,那么它什么时候为正,什么时候为负?
投影:
投影也是一个数量,不是向量;
当?为锐角时投影为正值;
当?为钝角时投影为负值;
当?为直角时投影为0;
由向量数量积的定义,试完成下面问题:
0
≤
证明向量
垂直的依据
解:
数量积的几何意义:
数量积的运算规律:
数量积的运算规律:
不成立
探究:两个向量的数量积与数的乘法有很大区别
(1)两个向量的数量积是一个实数,不是向量,符号由cos?的符号所决定.
解:
解:
(1)
(2)
解:
即
1、数量积的概念
2、数量积几何意义
3、重要性质
4、运算律
1、判断下列各题正确与否:
(1)若 ,则对任一向量 ,有 ( )
(2)若 ,则对任一非零向量 ,有 ( )
(3)若 , ,则 . ( )
(4)若 ,则 至少有一个为零. ( )
√
×
×
×
×
×
×
√
18或-2
D
5、若向量 与 的夹角为60°,
则 向量的模( )
A.2 B.4 C.6 D.12
C
1、
2、
时,△ABC为钝角三角形;
时,△ABC为直角三角形;
3.
投影分别为 投影如图.
