2.4.2平面向量数量积的坐标表示(共28张PPT)
文档属性
| 名称 | 2.4.2平面向量数量积的坐标表示(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 723.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
2.4.2 平面向量数量积的坐标表示、模、夹角
已知:
求:
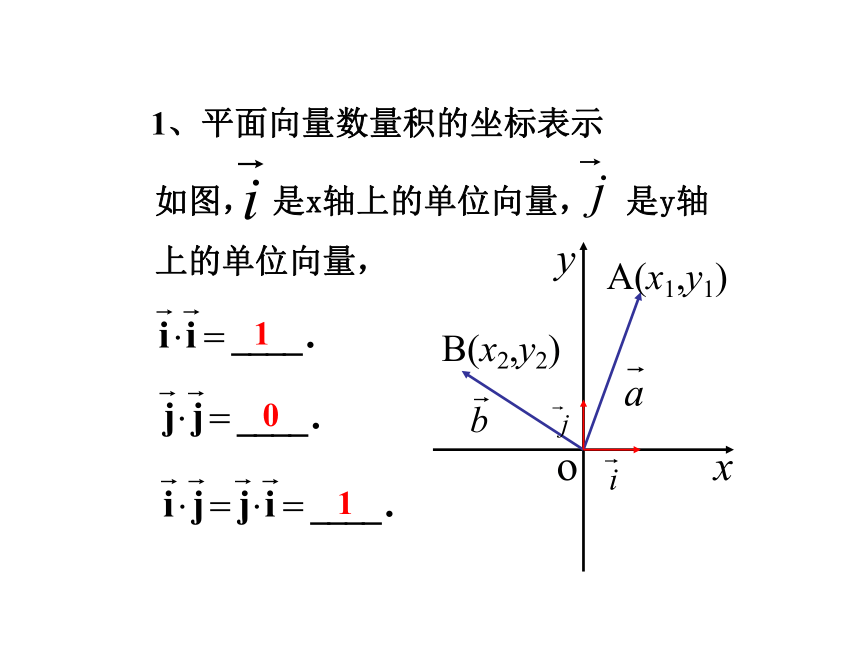
如图, 是x轴上的单位向量, 是y轴上的单位向量,
1
1
0
1、平面向量数量积的坐标表示
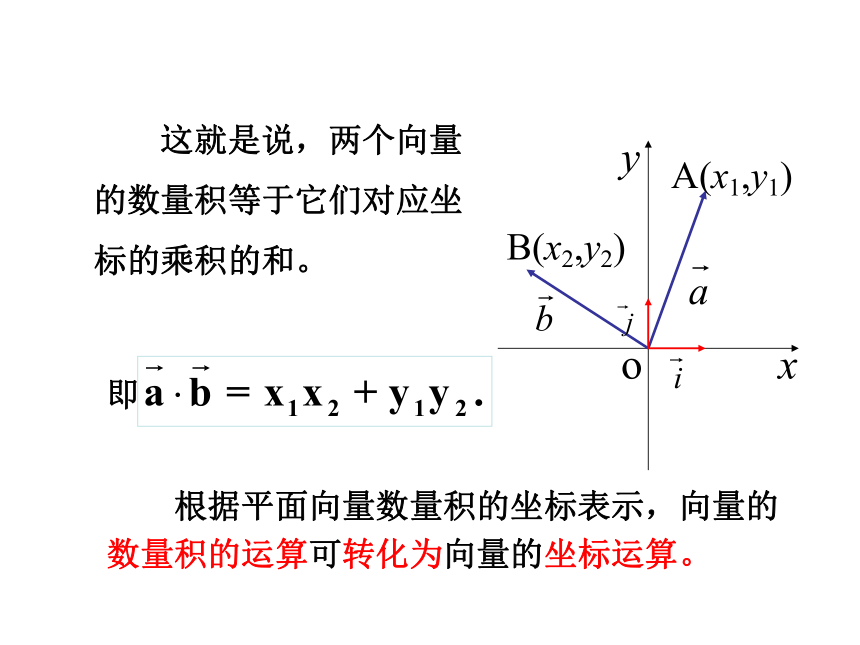
这就是说,两个向量的数量积等于它们对应坐标的乘积的和。
根据平面向量数量积的坐标表示,向量的数量积的运算可转化为向量的坐标运算。
即
2、向量的模和两点间的距离公式
(1)垂直
3、两向量垂直和平行的坐标表示
(2)平行
4、两向量夹角公式的坐标运算
例1:设 求 .
a 、b 夹角的余弦值?
解:
解:
例3:已知A(1,2),B(2,3),C(-2,5),试判断?ABC的形状,并给出证明.
在平面直角坐标系中,我们标出A(1,2),B(2,3),C(-2,5)三点,发现△ABC是直角三角形.
解:
证明:
∴△ABC是直角三角形.
例4:求 与向量的夹角为45°的单位向量.
解:
例5:(1)已知 =(4,3),向量 是垂直于 的单位向量,求 .
1、数量积的运算转化为向量的坐标运算;
2、掌握向量的模、距离、垂直、平行及夹角公式,形成转化技能。
(3)向量垂直
(4)向量平行
(5)两向量夹角公式的坐标运算
3、理解各公式的正向及逆向运用;
2
17
-3
3、已知A(1,2)、B(4、0)、C(8,6)、D(5,8),则四边形ABCD的形状是_________.
矩形
- 1
8、以原点和A(5,2)为两个顶点作等腰直角三角形OAB,?B=90?,求点B的坐标.
y
B
A
O
x
2.4.2 平面向量数量积的坐标表示、模、夹角
已知:
求:
如图, 是x轴上的单位向量, 是y轴上的单位向量,
1
1
0
1、平面向量数量积的坐标表示
这就是说,两个向量的数量积等于它们对应坐标的乘积的和。
根据平面向量数量积的坐标表示,向量的数量积的运算可转化为向量的坐标运算。
即
2、向量的模和两点间的距离公式
(1)垂直
3、两向量垂直和平行的坐标表示
(2)平行
4、两向量夹角公式的坐标运算
例1:设 求 .
a 、b 夹角的余弦值?
解:
解:
例3:已知A(1,2),B(2,3),C(-2,5),试判断?ABC的形状,并给出证明.
在平面直角坐标系中,我们标出A(1,2),B(2,3),C(-2,5)三点,发现△ABC是直角三角形.
解:
证明:
∴△ABC是直角三角形.
例4:求 与向量的夹角为45°的单位向量.
解:
例5:(1)已知 =(4,3),向量 是垂直于 的单位向量,求 .
1、数量积的运算转化为向量的坐标运算;
2、掌握向量的模、距离、垂直、平行及夹角公式,形成转化技能。
(3)向量垂直
(4)向量平行
(5)两向量夹角公式的坐标运算
3、理解各公式的正向及逆向运用;
2
17
-3
3、已知A(1,2)、B(4、0)、C(8,6)、D(5,8),则四边形ABCD的形状是_________.
矩形
- 1
8、以原点和A(5,2)为两个顶点作等腰直角三角形OAB,?B=90?,求点B的坐标.
y
B
A
O
x
