必修4第二章平面向量章末复习(共19张PPT)
文档属性
| 名称 | 必修4第二章平面向量章末复习(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 464.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 11:39:17 | ||
图片预览

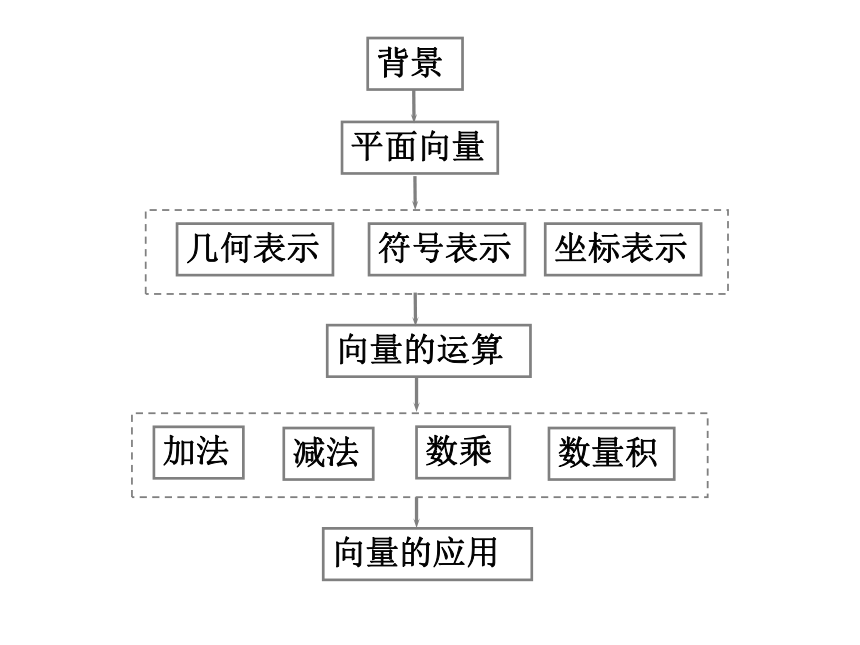





文档简介
(共19张PPT)
第二章 平面向量
2.1平面向量的实际背景及基本概念
2.2平面向量的线性运算
2.3平面向量的基本定理及坐标表示
2.4平面向量的数量积
2.5平面向量应用举例
1、从向量的物理背景、几何背景入手引出向量的概念,从而更好的把握向量的特点。
2、通过类比数的运算从而引出向量的加法运算、减法运算、数乘运算。
3、通过物理学中功W引出向量的数量级的定义。
向量:既有大小、又有方向的量叫做向量。
注:向量有两个要素,大小和方向,二者缺一不可。
2.1平面向量的实际背景及基本概念
1、一个概念: 向量的和
2、两个法则: 向量加法的三角形法则和平行四边形法则
3、两条运算律:
向量加法的交换律
结合律
2.2.1向量加法运算及其几何意义
1、理解相反向量的概念
2、理解向量减法的定义
3、正确理解掌握根据作定义向量减法。
4、正确熟练地掌握向量减法的三角形法则。
2.2.2向量减法运算及其几何意义
1、实数与向量可以相乘,其积仍是向量,但实数与向量不能相加、相减.实数除以向量没有意义,向量除以非零实数就是数乘向量。
2.2.3向量数乘运算及其几何意义
1、平面向量的基本定理
2.3平面向量的基本定理及坐标表示
2、向量的坐标表示是一种向量与坐标的对应关系,它使得向量具有代数意义.将向量的起点平移到坐标原点,则平移后向量的终点坐标就是向量的坐标。
3、向量的坐标运算是根据向量的坐标表示和向量的线性运算律得出的结论,它符合实数的运算规律,并使得向量的运算完全代数化。
4、向量平行(共线)充要条件的两种形式:
1、数量积的概念
2.4平面向量的数量积
2、数量积几何意义
3、重要性质
4、运算律
5、数量积的运算转化为向量的坐标运算:
用向量方法解决平面几何问题的“三步曲”:
(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
2.5平面向量应用举例
(2)通过向量运算,研究几何元素之间的关系,如距离、夹角等问题;
(3)把运算结果“翻译”成几何元素。
向量线性运算的结果是向量,而数量积的结果则是数,这个数值的大小不仅和向量与的模有关,还和它们的夹角有关。
1、平面向量的数量积
平面向量的应用,体现在高考中主要是在几何中的应用,由于平面向量的线性运算和数量积运算具有鲜明的几何背景,平面几何中的许多性质,如平移、全等、相似、长度(距离)、夹角等都可以用向量的线性运算及数量积表示出来,因此,可用向量的语言和方法来表述和解决几何中的一些问题。
2、向量的应用
1、对两向量夹角概念理解错误。
2、对向量数量积的运算律理解不透彻。
3、忽略共线向量。
第二章 平面向量
2.1平面向量的实际背景及基本概念
2.2平面向量的线性运算
2.3平面向量的基本定理及坐标表示
2.4平面向量的数量积
2.5平面向量应用举例
1、从向量的物理背景、几何背景入手引出向量的概念,从而更好的把握向量的特点。
2、通过类比数的运算从而引出向量的加法运算、减法运算、数乘运算。
3、通过物理学中功W引出向量的数量级的定义。
向量:既有大小、又有方向的量叫做向量。
注:向量有两个要素,大小和方向,二者缺一不可。
2.1平面向量的实际背景及基本概念
1、一个概念: 向量的和
2、两个法则: 向量加法的三角形法则和平行四边形法则
3、两条运算律:
向量加法的交换律
结合律
2.2.1向量加法运算及其几何意义
1、理解相反向量的概念
2、理解向量减法的定义
3、正确理解掌握根据作定义向量减法。
4、正确熟练地掌握向量减法的三角形法则。
2.2.2向量减法运算及其几何意义
1、实数与向量可以相乘,其积仍是向量,但实数与向量不能相加、相减.实数除以向量没有意义,向量除以非零实数就是数乘向量。
2.2.3向量数乘运算及其几何意义
1、平面向量的基本定理
2.3平面向量的基本定理及坐标表示
2、向量的坐标表示是一种向量与坐标的对应关系,它使得向量具有代数意义.将向量的起点平移到坐标原点,则平移后向量的终点坐标就是向量的坐标。
3、向量的坐标运算是根据向量的坐标表示和向量的线性运算律得出的结论,它符合实数的运算规律,并使得向量的运算完全代数化。
4、向量平行(共线)充要条件的两种形式:
1、数量积的概念
2.4平面向量的数量积
2、数量积几何意义
3、重要性质
4、运算律
5、数量积的运算转化为向量的坐标运算:
用向量方法解决平面几何问题的“三步曲”:
(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
2.5平面向量应用举例
(2)通过向量运算,研究几何元素之间的关系,如距离、夹角等问题;
(3)把运算结果“翻译”成几何元素。
向量线性运算的结果是向量,而数量积的结果则是数,这个数值的大小不仅和向量与的模有关,还和它们的夹角有关。
1、平面向量的数量积
平面向量的应用,体现在高考中主要是在几何中的应用,由于平面向量的线性运算和数量积运算具有鲜明的几何背景,平面几何中的许多性质,如平移、全等、相似、长度(距离)、夹角等都可以用向量的线性运算及数量积表示出来,因此,可用向量的语言和方法来表述和解决几何中的一些问题。
2、向量的应用
1、对两向量夹角概念理解错误。
2、对向量数量积的运算律理解不透彻。
3、忽略共线向量。
