【好题必练】17.2.1 平面直角坐标系同步练习题(含答案)
文档属性
| 名称 | 【好题必练】17.2.1 平面直角坐标系同步练习题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 00:00:00 | ||
图片预览


文档简介
第17章 函数及其图象
17.2 函数的图象
课时1 平面直角坐标系
/
知识点1 平面直角坐标系及有关概念
【核心提示1】在平面上画两条原点重合.互相垂直且具有相同单位长度的数轴,这就建立了 .通常把其中水平的数轴叫做 或 ,取 为正方向.铅直的数轴叫做 或 ,取 为正方向.两条数轴的交点O叫做 .在平面直角坐标系中,任意一点都可以用一对 来表示.
1.在图中的方格纸上有A、B、C、D四点(每个小方格的边长为1个单位长度),自己建立平面直角坐标系,分别写在点A、B、C、D的坐标.
/
2.如果电影院中“五排七号”记作(5,7),那么(3,4)表示的意义是 .
知识点2 平面坐标系中点的坐标特征
【核心提示2】点在直角坐标系的四个象限中的坐标特征如下:点P(x,y)在第一象限,x 0,y 0;点P(x,y)在第二象限,x 0,y 0;点P(x,y)在第三象限,x 0,y 0;点P(x,y)在第四象限,x 0,y 0.
3.点A(-5,6)所在象限为( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.若点A(m,n)在第二象限,则( )
A.m>0,n>0 B.m>0,n<0
C.m<0,n>0 D.m<0,n<0
5.在平面坐标系中,点M的坐标(0,-6),则下列说法正确的是( )
A.点M在x轴的正半轴上
B.点M在x轴的负半轴上
C.点M在y轴的正半轴上
D.点M在y轴的负半轴上
知识点3 点到坐标轴的距离与同一坐标轴上两点间的距离
【核心提示3】点P(a,b)到两坐标轴的距离:x轴的距离为 ,到y轴的距离为 .x轴上两点间的距离:点A(x1,0)和点B(x2,0)在x轴上,则点A、B之间的距离为 .点A(0,y1)和点B(0,y2)在y轴上,则点A、B之间的距离为 .
6.观察下面的平面直角坐标系,填一填.
(1)在平面直角坐标系中,A、B点的位置如图所示,试写出A、B两点的坐标:___________.
(2)若C(-3,-4)、D(3,-3),请在图示坐标系中标出C、D两点.
(3)试写出A、B、C、D四点到x轴和y轴的距离:
A______到x轴距离为______,到y轴距离为______.
B______到x轴距离为______,到y轴距离为______.
C(-3,-4)到x轴距离为______,到y轴距离为______.
D(3,-3)到x轴距离为______,到y轴距离为______.
(4)分析(3)中点的坐标与该点到坐标轴的距离的关系,利用你所发现的结论写出点P(x,y)到x轴的距离为______,到y轴距离为______.
7.点(-7,-8)到x轴的距离是( )
A.-7 B.8 C.7 D.-8
8.点C在x轴的上方,y轴的左侧,距离x轴2个单位长度,距离y轴3个单位长度,则点C的坐标为( )
A.(2,3) B.(-2,-3)
C.(-3,2) D.(3,-2)
9.如果点P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为 .
/
10.点P(-5,6)关于y轴对称的点的坐标是 .
11.点M(-2,3)与点N(2,3)关于 对称;点A(-2,-4)与点B(2,4)关于 对称;点G(4,0)雨点H(-4,0)关于 对称或 对称.
12.如果点M(3,x)在第一象限,则x的取值范围是 .
13.(河北)若点B(a,b)在第三象限,则点C(-a+1,3b-5)在第 象限.
14.如图,△ABC的三个顶点都在方格纸的格点上,其中点A的坐标是(-1,0),现将△ABC顺时针旋转90°,则旋转后点C的坐标是 .
15.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A(-2,1)和B(-2,-3),那么第一架轰炸机C的平面坐标是__________.
16.在平面直角坐标系中中,把点P(-5,-2)先向左平移两个单位长度,再向上平移4个单位长度后得到的点的坐标是( )
A.(-3,2) B.(-7,-6)
C.(-7,2) D.(-3,-6)
17.在平面直角坐标系中,点P(m-3,4-2m)不可能在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
18.(山东菏泽)若点M(x,y)满足(x+y)2=x2+y2-2,则点M所在的象限是( )
A.第一象限或第三象限
B.第二象限或第四象限
C.第三象限或第二象限
D.不能确定
19.(辽宁沈阳)如果|3x+3|+|x+3y-2|=0,那么点P(x,y)在第几象限?点Q(x+1,y-1)在坐标平面内的什么位置?
20.已知点A(2m,-3)与点B(6,1-n)关于原点对称,则m-n的值是多少?
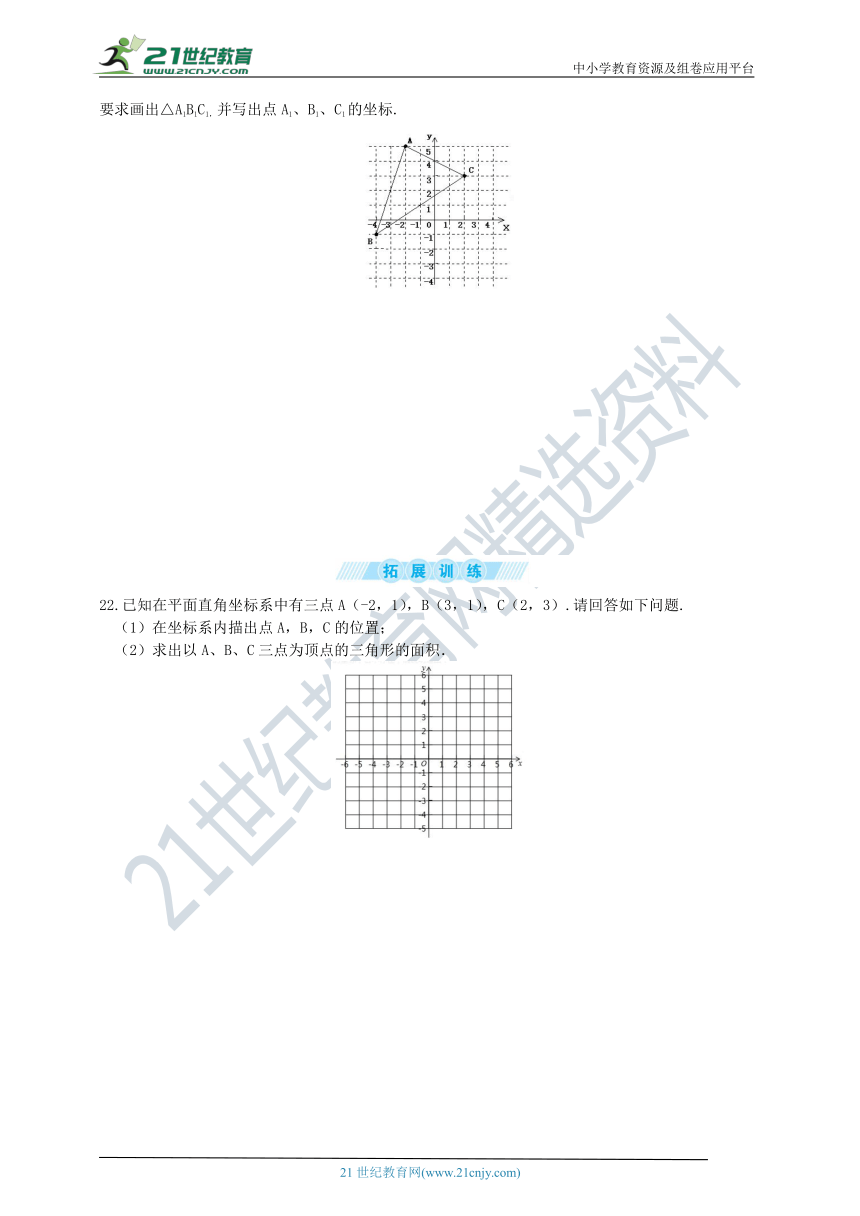
21.如图,将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的△A1B1C1.按要求画出△A1B1C1,并写出点A1、B1、C1的坐标.
/
/
22.已知在平面直角坐标系中有三点A(-2,1),B(3,1),C(2,3).请回答如下问题.
(1)在坐标系内描出点A,B,C的位置;
(2)求出以A、B、C三点为顶点的三角形的面积.
/
参 考 答 案
核心提示1 平面直角坐标系 x轴 横轴 向右 y轴 纵轴 向上 坐标原点 有序实数
1.示例:建立如图所示的坐标系:
/
坐标为:A(-1,5)、B(2,2)、C(0,0)、D(3,1).
2.三排四号
核心提示2 > > < > < < > <
3.B
4.C
5.D
核心提示3 |a| |b| |x2-x1| |y2-y1|
6.(1)A(2,4),B(-4,2)
(2)点C、D如图所示;
/
(3)(2,4) 4 (-4,2) 2 4 4 3 3 3
(4)|y| |x|
7.B
8.C
9.(3,4)、(-3,4)(3,-4)、(-3,-4)
10.(-5,6)
11.y轴 原点 原点 y轴
12.x>0
13.四
14.(2,1)
15.(2,-1)
16.C
17.A
18.B
19.解:根据题意可得,3x+3=0,x+3y-2=0,解得x=-1,y=1.
∴点P(-1,1)在第二象限.
∴点Q(x+1,y-1)的坐标为(0,0),
∴点Q在原点处.
20.解:∵点A、B关于原点对称,
∴2m=6,1-n=3,即m=-3,n=-2.
∴m-n=-3-(-2)=-1.
21.
/
坐标为:A1(0,2),B1(-2,-4)C1(4,0).
22.(1)
/
(2)依题意,得AB∥x轴,且AB=3-(-2)=5,
∴S△ABC=×5×2=5.
/
17.2 函数的图象
课时1 平面直角坐标系
/
知识点1 平面直角坐标系及有关概念
【核心提示1】在平面上画两条原点重合.互相垂直且具有相同单位长度的数轴,这就建立了 .通常把其中水平的数轴叫做 或 ,取 为正方向.铅直的数轴叫做 或 ,取 为正方向.两条数轴的交点O叫做 .在平面直角坐标系中,任意一点都可以用一对 来表示.
1.在图中的方格纸上有A、B、C、D四点(每个小方格的边长为1个单位长度),自己建立平面直角坐标系,分别写在点A、B、C、D的坐标.
/
2.如果电影院中“五排七号”记作(5,7),那么(3,4)表示的意义是 .
知识点2 平面坐标系中点的坐标特征
【核心提示2】点在直角坐标系的四个象限中的坐标特征如下:点P(x,y)在第一象限,x 0,y 0;点P(x,y)在第二象限,x 0,y 0;点P(x,y)在第三象限,x 0,y 0;点P(x,y)在第四象限,x 0,y 0.
3.点A(-5,6)所在象限为( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.若点A(m,n)在第二象限,则( )
A.m>0,n>0 B.m>0,n<0
C.m<0,n>0 D.m<0,n<0
5.在平面坐标系中,点M的坐标(0,-6),则下列说法正确的是( )
A.点M在x轴的正半轴上
B.点M在x轴的负半轴上
C.点M在y轴的正半轴上
D.点M在y轴的负半轴上
知识点3 点到坐标轴的距离与同一坐标轴上两点间的距离
【核心提示3】点P(a,b)到两坐标轴的距离:x轴的距离为 ,到y轴的距离为 .x轴上两点间的距离:点A(x1,0)和点B(x2,0)在x轴上,则点A、B之间的距离为 .点A(0,y1)和点B(0,y2)在y轴上,则点A、B之间的距离为 .
6.观察下面的平面直角坐标系,填一填.
(1)在平面直角坐标系中,A、B点的位置如图所示,试写出A、B两点的坐标:___________.
(2)若C(-3,-4)、D(3,-3),请在图示坐标系中标出C、D两点.
(3)试写出A、B、C、D四点到x轴和y轴的距离:
A______到x轴距离为______,到y轴距离为______.
B______到x轴距离为______,到y轴距离为______.
C(-3,-4)到x轴距离为______,到y轴距离为______.
D(3,-3)到x轴距离为______,到y轴距离为______.
(4)分析(3)中点的坐标与该点到坐标轴的距离的关系,利用你所发现的结论写出点P(x,y)到x轴的距离为______,到y轴距离为______.
7.点(-7,-8)到x轴的距离是( )
A.-7 B.8 C.7 D.-8
8.点C在x轴的上方,y轴的左侧,距离x轴2个单位长度,距离y轴3个单位长度,则点C的坐标为( )
A.(2,3) B.(-2,-3)
C.(-3,2) D.(3,-2)
9.如果点P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为 .
/
10.点P(-5,6)关于y轴对称的点的坐标是 .
11.点M(-2,3)与点N(2,3)关于 对称;点A(-2,-4)与点B(2,4)关于 对称;点G(4,0)雨点H(-4,0)关于 对称或 对称.
12.如果点M(3,x)在第一象限,则x的取值范围是 .
13.(河北)若点B(a,b)在第三象限,则点C(-a+1,3b-5)在第 象限.
14.如图,△ABC的三个顶点都在方格纸的格点上,其中点A的坐标是(-1,0),现将△ABC顺时针旋转90°,则旋转后点C的坐标是 .
15.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A(-2,1)和B(-2,-3),那么第一架轰炸机C的平面坐标是__________.
16.在平面直角坐标系中中,把点P(-5,-2)先向左平移两个单位长度,再向上平移4个单位长度后得到的点的坐标是( )
A.(-3,2) B.(-7,-6)
C.(-7,2) D.(-3,-6)
17.在平面直角坐标系中,点P(m-3,4-2m)不可能在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
18.(山东菏泽)若点M(x,y)满足(x+y)2=x2+y2-2,则点M所在的象限是( )
A.第一象限或第三象限
B.第二象限或第四象限
C.第三象限或第二象限
D.不能确定
19.(辽宁沈阳)如果|3x+3|+|x+3y-2|=0,那么点P(x,y)在第几象限?点Q(x+1,y-1)在坐标平面内的什么位置?
20.已知点A(2m,-3)与点B(6,1-n)关于原点对称,则m-n的值是多少?
21.如图,将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的△A1B1C1.按要求画出△A1B1C1,并写出点A1、B1、C1的坐标.
/
/
22.已知在平面直角坐标系中有三点A(-2,1),B(3,1),C(2,3).请回答如下问题.
(1)在坐标系内描出点A,B,C的位置;
(2)求出以A、B、C三点为顶点的三角形的面积.
/
参 考 答 案
核心提示1 平面直角坐标系 x轴 横轴 向右 y轴 纵轴 向上 坐标原点 有序实数
1.示例:建立如图所示的坐标系:
/
坐标为:A(-1,5)、B(2,2)、C(0,0)、D(3,1).
2.三排四号
核心提示2 > > < > < < > <
3.B
4.C
5.D
核心提示3 |a| |b| |x2-x1| |y2-y1|
6.(1)A(2,4),B(-4,2)
(2)点C、D如图所示;
/
(3)(2,4) 4 (-4,2) 2 4 4 3 3 3
(4)|y| |x|
7.B
8.C
9.(3,4)、(-3,4)(3,-4)、(-3,-4)
10.(-5,6)
11.y轴 原点 原点 y轴
12.x>0
13.四
14.(2,1)
15.(2,-1)
16.C
17.A
18.B
19.解:根据题意可得,3x+3=0,x+3y-2=0,解得x=-1,y=1.
∴点P(-1,1)在第二象限.
∴点Q(x+1,y-1)的坐标为(0,0),
∴点Q在原点处.
20.解:∵点A、B关于原点对称,
∴2m=6,1-n=3,即m=-3,n=-2.
∴m-n=-3-(-2)=-1.
21.
/
坐标为:A1(0,2),B1(-2,-4)C1(4,0).
22.(1)
/
(2)依题意,得AB∥x轴,且AB=3-(-2)=5,
∴S△ABC=×5×2=5.
/
