【好题必练】17.3.4 一次函数的表达式同步练习题(含答案)
文档属性
| 名称 | 【好题必练】17.3.4 一次函数的表达式同步练习题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 18:47:56 | ||
图片预览


文档简介
第17章 函数及其图象
17.3 一次函数
课时4 一次函数的表达式
知识点 用待定系数法求一次函数的表达式
【核心提示1】先设待求函数表达式(其中含有待定系数),再根据条件列方程或方程组,求出 ,从而得到所求结果的方法,叫做 .用待定系数法求一次函数表达式的一般步骤:①设:设出 的表达式;②列:将已知条件中两个点的坐标代入函数表达式中,列出关于待定系数的 或 ;③解:解方程或方程组,得到待定系数的值;④还原:将 代回所设的函数表达式中,即可得到 .
1.一次函数y=kx+b中,当x=1时,y=3;当x=-1时,y=2,则k= ,b= .
2.一条直线经过点(1,5)且与直线y=x平行,则它的函数关系式是 .
3.点(11,5) (填“在”或“不在”)经过A(1,-2),B(-2,1)两点的直线上.
4.(浙江湖州)已知y是x的一次函数,当x=3时,y=1;当x=-2时,y=-4,这个一次函数的解析式是 .
5.(青海西宁)若点A(m,n)在直线y=kx+b(k≠0)上,当-1≤m≤1时,-1≤n≤1,则这条直线的函数解析式为 .
6.若一次函数y=kx+17的图象经过点(-3,2),则k的值为( )
A.-6 B.6 C.-5 D.5
7.函数y=kx+2经过点(1,3),则y=0时,x=( )
A.-2 B.2 C.0 D.±2
8.如图,若点P(-2,4)关于y轴的对称点在一次函数y=x+b的图象上,则b的值为( )
A.-2 B.2
C.-6 D.6
9.如果一次函数y=kx+b的图象经过点(2,-1)和(0,3),那么这个一次函数的表达式为( )
A.y=-2x+3 B.y=-3x+2
C.y=3x-2 D.y=x-3
10.(黑龙江绥化)在同一平面直角坐标系中,直线y=4x+1与直线y=-x+b的交点不可能在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
11.已知一次函数y=kx+2,当x=-1时,y=1,求此函数的表达式.
12.如图,在平面直角坐标系中,正方形ABCD的对称中心与原点重合,顶点A的坐标为(-1,1),顶点B在第一象限,若点B在直线y=kx+3上,则k的值为 .
13.如图,在直角坐标系中,已知矩形ABCO的两个顶点A(3,0),B(3,2),对角线AC所在的直线l对应的解析式是 .
14.已知A,B两地相距100千米,甲乙两人分别从A,B两地同时骑车相向而行.假设他们都保持匀速行驶.甲、乙两人离A地的距离s(千米)与骑车时间t(时间)满足的函数关系图象如图所示.当甲、乙两人相遇时,乙距离A地 千米.
15.如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是( )
A.y=2x+3 B.y=x-3
C.y=2x-3 D.y=-x+3
16.一次函数y=kx+b的图象如图,则( )
A. B.
C. D.
17.一次函数y=-3x+b和y=kx+1的图象如图所示,其交点为P(3,4),则不等式kx+1≥-3x+b的解集在数轴上表示正确的是( )
18.已知y是关于x的一次函数,当x=0时,y=3;当x=2时,y=7.
(1)求这个一次函数的表达式;
(2)当x=4时,求y的值;
(3)当y=4时,求x的值.
19.一次函数y=kx+4的图象经过点(-3,-2).
(1)求这个函数的解析式;
(2)画出该函数的图象;
(3)判断点(3,5)是否在此函数的图象上.
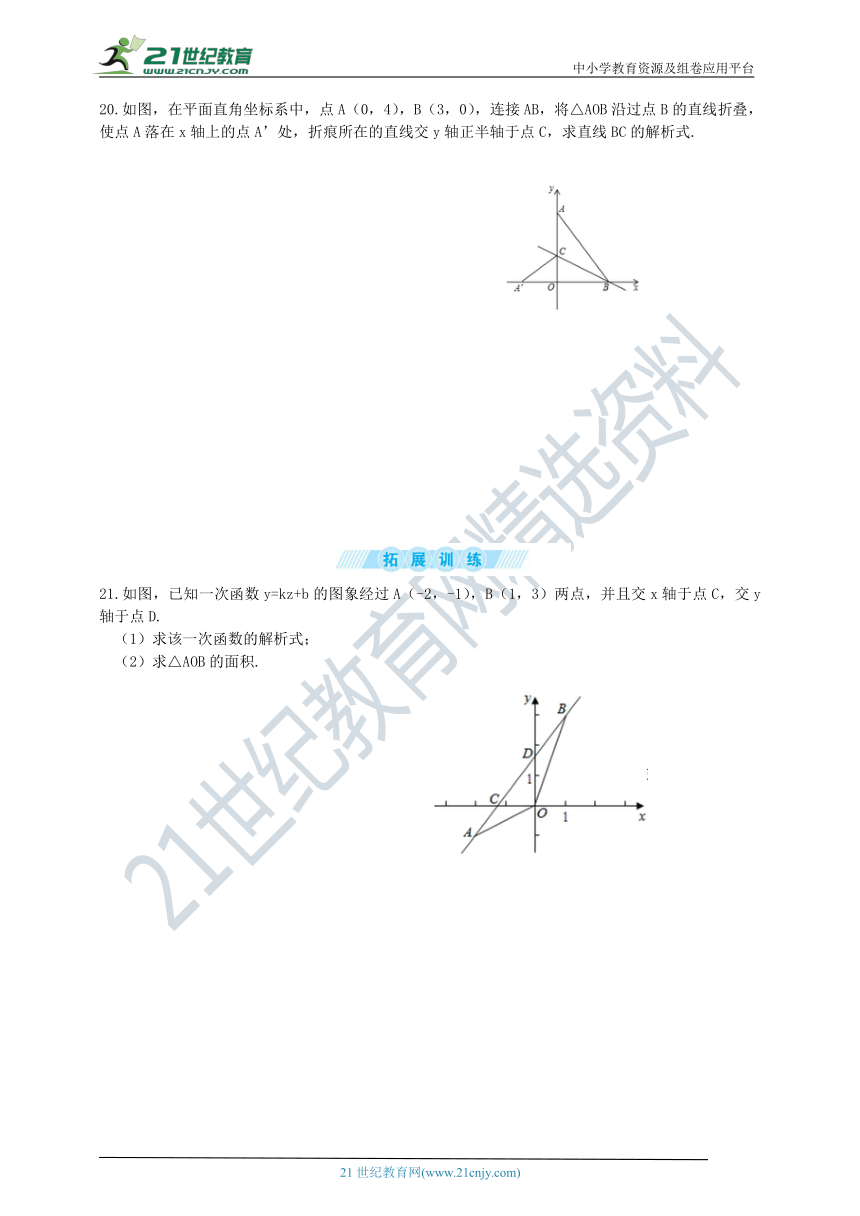
20.如图,在平面直角坐标系中,点A(0,4),B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A’处,折痕所在的直线交y轴正半轴于点C,求直线BC的解析式.
21.如图,已知一次函数y=kz+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D.
(1)求该一次函数的解析式;
(2)求△AOB的面积.
参 考 答 案
核心提示 待定系数 待定系数法 待求函数 方程 方程组 求出的待定系数的值 所求函数的表达式
1.
2.y=x+4
3.不在
4.y=x-2
5.y=x或y=-x
6.D
7.A
8.B
9.A
10.D
11.解:y=x+2.
12.-2
13.y=-x+2
14.
15.D
16.D
17.B
18.解:(1)设一次函数表达式为y=kx+b(k≠0).
分别把x=0,y=3;x=2,y=7代入y=kx+b,
得
即这个函数的表达式为y=2x+3.
(2)把x=4代入y=2x+3,得y=2×4+3=11.
(3)把y=4代入y=2x+3,得4=2x+3,解得x=.
19.解:(1)把(-3,-2)代入y=kx+4得-3k+4=-2,解得k=2,所以一次函数解析式为y=2x+4.
(2)如下图,
(3)当x=3时,y=2x+4=6+4=10, 所以点(3,5)不在此函数的图象上.
20.解:∵A(0,4),B(3,0),∴OA=4,OB=3,
在Rt△OAB中,AB==5.
依题,BA’=BA=5,CA’=CA,
∴OA’=BA’-OB=5-3=2, 设0C=t,则CA=CA’=4-t, 在Rt△OA’C中,0C2+OA’2=CA’2, ∴t2+22=(4-t)2,解得t=,∴C点坐标为(0,), 设直线BC的解析式为y=kx+b, 把B(3,0),C(0,)代人得,解得,
∴直线BC的解析式为y=-x+.
21.解:(1)把A(-2,-1),B(1,3)代入y=kx+b得, 解得 所以一次函数的解析式为y=x+. (2)把x=0代入y=x+得x=, 所以D点坐标为(0,), 所以△AOB的面积为 S△A0D+S△BOD=××2+××1=.
17.3 一次函数
课时4 一次函数的表达式
知识点 用待定系数法求一次函数的表达式
【核心提示1】先设待求函数表达式(其中含有待定系数),再根据条件列方程或方程组,求出 ,从而得到所求结果的方法,叫做 .用待定系数法求一次函数表达式的一般步骤:①设:设出 的表达式;②列:将已知条件中两个点的坐标代入函数表达式中,列出关于待定系数的 或 ;③解:解方程或方程组,得到待定系数的值;④还原:将 代回所设的函数表达式中,即可得到 .
1.一次函数y=kx+b中,当x=1时,y=3;当x=-1时,y=2,则k= ,b= .
2.一条直线经过点(1,5)且与直线y=x平行,则它的函数关系式是 .
3.点(11,5) (填“在”或“不在”)经过A(1,-2),B(-2,1)两点的直线上.
4.(浙江湖州)已知y是x的一次函数,当x=3时,y=1;当x=-2时,y=-4,这个一次函数的解析式是 .
5.(青海西宁)若点A(m,n)在直线y=kx+b(k≠0)上,当-1≤m≤1时,-1≤n≤1,则这条直线的函数解析式为 .
6.若一次函数y=kx+17的图象经过点(-3,2),则k的值为( )
A.-6 B.6 C.-5 D.5
7.函数y=kx+2经过点(1,3),则y=0时,x=( )
A.-2 B.2 C.0 D.±2
8.如图,若点P(-2,4)关于y轴的对称点在一次函数y=x+b的图象上,则b的值为( )
A.-2 B.2
C.-6 D.6
9.如果一次函数y=kx+b的图象经过点(2,-1)和(0,3),那么这个一次函数的表达式为( )
A.y=-2x+3 B.y=-3x+2
C.y=3x-2 D.y=x-3
10.(黑龙江绥化)在同一平面直角坐标系中,直线y=4x+1与直线y=-x+b的交点不可能在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
11.已知一次函数y=kx+2,当x=-1时,y=1,求此函数的表达式.
12.如图,在平面直角坐标系中,正方形ABCD的对称中心与原点重合,顶点A的坐标为(-1,1),顶点B在第一象限,若点B在直线y=kx+3上,则k的值为 .
13.如图,在直角坐标系中,已知矩形ABCO的两个顶点A(3,0),B(3,2),对角线AC所在的直线l对应的解析式是 .
14.已知A,B两地相距100千米,甲乙两人分别从A,B两地同时骑车相向而行.假设他们都保持匀速行驶.甲、乙两人离A地的距离s(千米)与骑车时间t(时间)满足的函数关系图象如图所示.当甲、乙两人相遇时,乙距离A地 千米.
15.如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是( )
A.y=2x+3 B.y=x-3
C.y=2x-3 D.y=-x+3
16.一次函数y=kx+b的图象如图,则( )
A. B.
C. D.
17.一次函数y=-3x+b和y=kx+1的图象如图所示,其交点为P(3,4),则不等式kx+1≥-3x+b的解集在数轴上表示正确的是( )
18.已知y是关于x的一次函数,当x=0时,y=3;当x=2时,y=7.
(1)求这个一次函数的表达式;
(2)当x=4时,求y的值;
(3)当y=4时,求x的值.
19.一次函数y=kx+4的图象经过点(-3,-2).
(1)求这个函数的解析式;
(2)画出该函数的图象;
(3)判断点(3,5)是否在此函数的图象上.
20.如图,在平面直角坐标系中,点A(0,4),B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A’处,折痕所在的直线交y轴正半轴于点C,求直线BC的解析式.
21.如图,已知一次函数y=kz+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D.
(1)求该一次函数的解析式;
(2)求△AOB的面积.
参 考 答 案
核心提示 待定系数 待定系数法 待求函数 方程 方程组 求出的待定系数的值 所求函数的表达式
1.
2.y=x+4
3.不在
4.y=x-2
5.y=x或y=-x
6.D
7.A
8.B
9.A
10.D
11.解:y=x+2.
12.-2
13.y=-x+2
14.
15.D
16.D
17.B
18.解:(1)设一次函数表达式为y=kx+b(k≠0).
分别把x=0,y=3;x=2,y=7代入y=kx+b,
得
即这个函数的表达式为y=2x+3.
(2)把x=4代入y=2x+3,得y=2×4+3=11.
(3)把y=4代入y=2x+3,得4=2x+3,解得x=.
19.解:(1)把(-3,-2)代入y=kx+4得-3k+4=-2,解得k=2,所以一次函数解析式为y=2x+4.
(2)如下图,
(3)当x=3时,y=2x+4=6+4=10, 所以点(3,5)不在此函数的图象上.
20.解:∵A(0,4),B(3,0),∴OA=4,OB=3,
在Rt△OAB中,AB==5.
依题,BA’=BA=5,CA’=CA,
∴OA’=BA’-OB=5-3=2, 设0C=t,则CA=CA’=4-t, 在Rt△OA’C中,0C2+OA’2=CA’2, ∴t2+22=(4-t)2,解得t=,∴C点坐标为(0,), 设直线BC的解析式为y=kx+b, 把B(3,0),C(0,)代人得,解得,
∴直线BC的解析式为y=-x+.
21.解:(1)把A(-2,-1),B(1,3)代入y=kx+b得, 解得 所以一次函数的解析式为y=x+. (2)把x=0代入y=x+得x=, 所以D点坐标为(0,), 所以△AOB的面积为 S△A0D+S△BOD=××2+××1=.
