【好题必练】19.2.2 菱形的判定同步练习题(含答案)
文档属性
| 名称 | 【好题必练】19.2.2 菱形的判定同步练习题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 00:00:00 | ||
图片预览


文档简介
第19章 矩形、菱形与正方形
19.2 菱形
课时2 菱形的判定
/
知识点1 菱形的判定
【核心提示1】有一组临边相等的平行四边形是 .
1.如图,□ABCD的对角线,AC,BD相交于点O,请添加一个适当的条件 使其成为菱形(只填一个即可).
2.如图,要使ABCD成为菱形,则需添加的个条件是( )
A.AC=AD B.BA=BC
C.∠ABC=90° D.AC=BD
3.(贵州遵义)如图,在□ABCD中,对角线AC、BD交于点O,若增加一个条件,使□ABCD成为菱形,下列给出的条件不正确的是( )
A.AB=AD B.AC=BD
C.AC=BD D.∠BAC=∠DAC
4.在平行四边形ABCD中,AC和BD交于点0,添加如下条件:(1)∠AOB=90°;(2)∠ABD=∠CBD;(3)AB=BC;(4)OA=0B.其中平行四边形ABCD成为菱形的有( )
A.1个 B.2个 C.3个 D.4个
知识点2 菱形的判定定理1
【核心提示2】四条边都相等的四边形是 .
5.用两个全等的等腰三角形拼成一个四边形.该四边形一定是( )
A.菱形 B.菱形或一般的平行四边形
C.矩形 D.矩形或一般的平行四边形
6.下列四边形中不一定为菱形的是( )
A.对角线相等的平行四边形
B.每条对角线平分一组对角的四边形
C.对角线互相垂直的平行四边形
D.用两个全等的等边三角形拼成的四边形
7.如图,△ABC为等腰三角形,如果把它沿底边BC翻折后,得到△DBC,那边四边形ABDC为( )
A菱形 B正方形
C.矩形 D.一般平行四边形
8.如图,将△ABC沿BC方向平移得到△DCE,连接AD.下列条件中,能够判定四边形ACED为菱形的是( )
A.AB=BC B.AC=BC
C.∠ABC=60° D.∠ACB=60°
知识点3 菱形的判定定理2
【核心提示3】对角线互相垂直的平行四边形是 .
9.如图,在四边形ABCD中,对角线AC,BD交于点O,0A=0C,OB=0D,添加一个条件使四边形ABCD是菱形,那么所添加的条件可以是 (写出一个即可).
10.如图,D,E,F分别是△ABC的边BC,CA,AB上的点,且DE∥AB,DF∥CA,要使四边形AFDE是菱形,则要增加的条件是 .(只写出符合要求的一个即可)
11.(河南)如图,在□ABCD中,对角线AC、BD交于点O,添加下列条件不能判定□ABCD是菱形的只有( )
A.AC⊥BD B.AB=BC
C.AC=BD D.∠1=∠2
12.如图,已知四边形ABCD的对角线互相垂直,若适当添加一个条件,就能判定该四边形是菱形,那么这个条件可以是( )
A.BA=BC B.AC=BD
C.AB∥CD D.AC,BD互相平分
/
13.如图,在△ABC中,AB=AC,∠BAC=40?,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD,CE交于点F.
(1)求证:△ABD≌△ACE;
(2)求证:四边形ABFE是菱形.
/
14.如图,在四边形ABCD中,AB∥CD,AB=CD=BC,四边形ABCD是菱形吗?说明理由.
/
15.如图,四边形ABCD是矩形,直线l垂直平分线段AC,垂足为O,直线1分 别与线段AD,CB的延长线交于点E,F,求证:四边形AFCE是菱形.
/
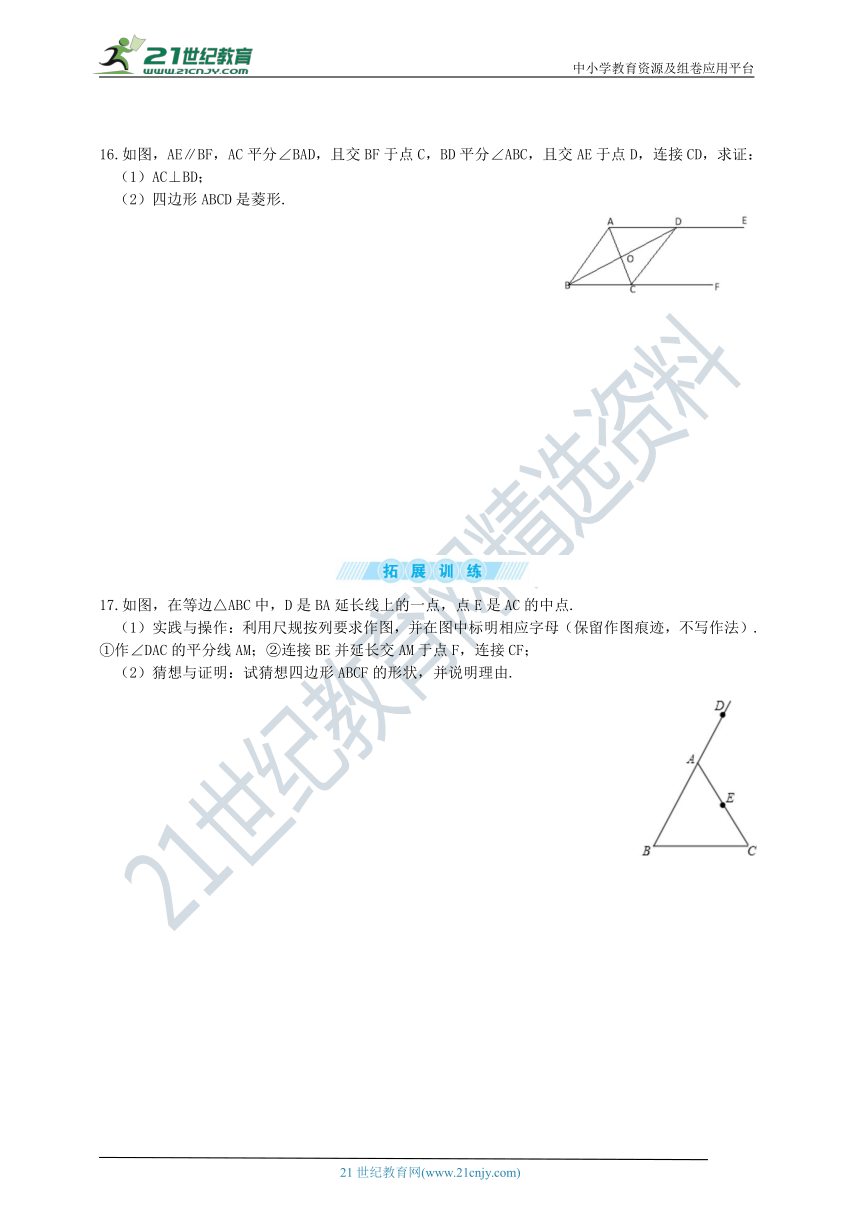
16.如图,AE∥BF,AC平分∠BAD,且交BF于点C,BD平分∠ABC,且交AE于点D,连接CD,求证:
(1)AC⊥BD;
(2)四边形ABCD是菱形.
/
/
17.如图,在等边△ABC中,D是BA延长线上的一点,点E是AC的中点.
实践与操作:利用尺规按列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法).①作∠DAC的平分线AM;②连接BE并延长交AM于点F,连接CF;
(2)猜想与证明:试猜想四边形ABCF的形状,并说明理由.
/
参 考 答 案
核心提示1 菱形
1.示例:AC⊥BD
2.B
3.C
4.C
核心提示2 菱形
5.B
6.A
7.A
8.B
核心提示3 菱形
9.示例:AC⊥BD
10.AE=AF
11.C
12.D
13.证明:(1)∵△ABC绕点A按逆时针方向旋转100,
∴∠BAC=∠DAE=40°,
∴∠BAD=∠CAE=100°.
又∵AB=AC,
∴AB=AC=AD=AE.
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS).
(2)∵∠BAD=∠CAE=100°,AB=AC=AD=AE,
∴∠ABD=∠ADB=∠ACE=∠AEC=40°.
∵∠BAE=∠BAD+∠DAE=140°,
∴∠BFE=360°-∠BAE-∠ABD-∠AEC=140°,
∴∠BAE=∠BFE,
∴四边形ABFE是平行四边形.
∵AB=AE,
∴□ABFE是菱形
14.解:四边形ABCD是菱形.
理由:因为四边形ABCD中,AB∥CD,且AB=CD,
所以四边形ABCD是平行四边形.
又因为AB=BC,
所以四边形ABCD是菱形.
15.证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EAO=∠FCO,
在△AOE和△COF中,
,
∴△AOE≌△COF(ASA),
∴AE=FC,
∴四边形AFCE是平行四边形,
∵直线l垂直平分线段AC,
∴平行四边形AFCE是菱形.
16.证明:(1)∵AE∥BF,
∴∠BCA=∠CAD,
∵AC平分∠BAD,
∴BAC=∠CAD,
∴∠BCA=∠BAC,
∴△BAC是等腰三角形,
∵BD平分∠ABC,
∴AC⊥BD.
(2)∵△BAC是等腰三角形,
∴AB=CB,
∵∠CBD=∠ABD=∠BDA,
∴△ABD也是等腰三角形,
∴AB=AD,∴DA=CB,
∵BC∥DA,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴□ABCD是菱形.
17.解:(1)如答图所示.
/
(2)菱形.理由如下:
∵△ABC是等边三角形,
∴∠ABC=∠BAC=60°,
∴∠DAC=120°.
又∵AF平分∠DAC,
∴∠DAF=∠ABC=60°,
∴AF∥BC.
∵E为AC中点,
∴AE=EC,
在△AEF和△CEB中,,
∴△AEF≌△CEB(ASA),
∴AF=BC,
∴四边形ABCF是平行四边形,
又∵BE⊥AC,
∴□ABCF是菱形.
/
19.2 菱形
课时2 菱形的判定
/
知识点1 菱形的判定
【核心提示1】有一组临边相等的平行四边形是 .
1.如图,□ABCD的对角线,AC,BD相交于点O,请添加一个适当的条件 使其成为菱形(只填一个即可).
2.如图,要使ABCD成为菱形,则需添加的个条件是( )
A.AC=AD B.BA=BC
C.∠ABC=90° D.AC=BD
3.(贵州遵义)如图,在□ABCD中,对角线AC、BD交于点O,若增加一个条件,使□ABCD成为菱形,下列给出的条件不正确的是( )
A.AB=AD B.AC=BD
C.AC=BD D.∠BAC=∠DAC
4.在平行四边形ABCD中,AC和BD交于点0,添加如下条件:(1)∠AOB=90°;(2)∠ABD=∠CBD;(3)AB=BC;(4)OA=0B.其中平行四边形ABCD成为菱形的有( )
A.1个 B.2个 C.3个 D.4个
知识点2 菱形的判定定理1
【核心提示2】四条边都相等的四边形是 .
5.用两个全等的等腰三角形拼成一个四边形.该四边形一定是( )
A.菱形 B.菱形或一般的平行四边形
C.矩形 D.矩形或一般的平行四边形
6.下列四边形中不一定为菱形的是( )
A.对角线相等的平行四边形
B.每条对角线平分一组对角的四边形
C.对角线互相垂直的平行四边形
D.用两个全等的等边三角形拼成的四边形
7.如图,△ABC为等腰三角形,如果把它沿底边BC翻折后,得到△DBC,那边四边形ABDC为( )
A菱形 B正方形
C.矩形 D.一般平行四边形
8.如图,将△ABC沿BC方向平移得到△DCE,连接AD.下列条件中,能够判定四边形ACED为菱形的是( )
A.AB=BC B.AC=BC
C.∠ABC=60° D.∠ACB=60°
知识点3 菱形的判定定理2
【核心提示3】对角线互相垂直的平行四边形是 .
9.如图,在四边形ABCD中,对角线AC,BD交于点O,0A=0C,OB=0D,添加一个条件使四边形ABCD是菱形,那么所添加的条件可以是 (写出一个即可).
10.如图,D,E,F分别是△ABC的边BC,CA,AB上的点,且DE∥AB,DF∥CA,要使四边形AFDE是菱形,则要增加的条件是 .(只写出符合要求的一个即可)
11.(河南)如图,在□ABCD中,对角线AC、BD交于点O,添加下列条件不能判定□ABCD是菱形的只有( )
A.AC⊥BD B.AB=BC
C.AC=BD D.∠1=∠2
12.如图,已知四边形ABCD的对角线互相垂直,若适当添加一个条件,就能判定该四边形是菱形,那么这个条件可以是( )
A.BA=BC B.AC=BD
C.AB∥CD D.AC,BD互相平分
/
13.如图,在△ABC中,AB=AC,∠BAC=40?,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD,CE交于点F.
(1)求证:△ABD≌△ACE;
(2)求证:四边形ABFE是菱形.
/
14.如图,在四边形ABCD中,AB∥CD,AB=CD=BC,四边形ABCD是菱形吗?说明理由.
/
15.如图,四边形ABCD是矩形,直线l垂直平分线段AC,垂足为O,直线1分 别与线段AD,CB的延长线交于点E,F,求证:四边形AFCE是菱形.
/
16.如图,AE∥BF,AC平分∠BAD,且交BF于点C,BD平分∠ABC,且交AE于点D,连接CD,求证:
(1)AC⊥BD;
(2)四边形ABCD是菱形.
/
/
17.如图,在等边△ABC中,D是BA延长线上的一点,点E是AC的中点.
实践与操作:利用尺规按列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法).①作∠DAC的平分线AM;②连接BE并延长交AM于点F,连接CF;
(2)猜想与证明:试猜想四边形ABCF的形状,并说明理由.
/
参 考 答 案
核心提示1 菱形
1.示例:AC⊥BD
2.B
3.C
4.C
核心提示2 菱形
5.B
6.A
7.A
8.B
核心提示3 菱形
9.示例:AC⊥BD
10.AE=AF
11.C
12.D
13.证明:(1)∵△ABC绕点A按逆时针方向旋转100,
∴∠BAC=∠DAE=40°,
∴∠BAD=∠CAE=100°.
又∵AB=AC,
∴AB=AC=AD=AE.
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS).
(2)∵∠BAD=∠CAE=100°,AB=AC=AD=AE,
∴∠ABD=∠ADB=∠ACE=∠AEC=40°.
∵∠BAE=∠BAD+∠DAE=140°,
∴∠BFE=360°-∠BAE-∠ABD-∠AEC=140°,
∴∠BAE=∠BFE,
∴四边形ABFE是平行四边形.
∵AB=AE,
∴□ABFE是菱形
14.解:四边形ABCD是菱形.
理由:因为四边形ABCD中,AB∥CD,且AB=CD,
所以四边形ABCD是平行四边形.
又因为AB=BC,
所以四边形ABCD是菱形.
15.证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EAO=∠FCO,
在△AOE和△COF中,
,
∴△AOE≌△COF(ASA),
∴AE=FC,
∴四边形AFCE是平行四边形,
∵直线l垂直平分线段AC,
∴平行四边形AFCE是菱形.
16.证明:(1)∵AE∥BF,
∴∠BCA=∠CAD,
∵AC平分∠BAD,
∴BAC=∠CAD,
∴∠BCA=∠BAC,
∴△BAC是等腰三角形,
∵BD平分∠ABC,
∴AC⊥BD.
(2)∵△BAC是等腰三角形,
∴AB=CB,
∵∠CBD=∠ABD=∠BDA,
∴△ABD也是等腰三角形,
∴AB=AD,∴DA=CB,
∵BC∥DA,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴□ABCD是菱形.
17.解:(1)如答图所示.
/
(2)菱形.理由如下:
∵△ABC是等边三角形,
∴∠ABC=∠BAC=60°,
∴∠DAC=120°.
又∵AF平分∠DAC,
∴∠DAF=∠ABC=60°,
∴AF∥BC.
∵E为AC中点,
∴AE=EC,
在△AEF和△CEB中,,
∴△AEF≌△CEB(ASA),
∴AF=BC,
∴四边形ABCF是平行四边形,
又∵BE⊥AC,
∴□ABCF是菱形.
/
